Interior Distance Estimate algorithm for the Mandelbrot set

Question

I'm looking for a way to estimate the distance to the boundary of the Mandelbrot set from a point inside of it for use in a GLSL shader.

This page links to various resources online touching on the subject of interior distance estimation such as the underlying mathematical formula, a Haskell implementation, some other blogs, forum posts and a C99 implementation, but I got the impression that they are all either very complex to implement or very computationally heavy to run.

After many hours of trying, I managed to make this code that runs in Shadertoy:

void mainImage( out vec4 fragColor, in vec2 fragCoord ) {

    float zoom = 1.;
    vec2 c = vec2(-0.75, 0.0) + zoom * (2.*fragCoord-iResolution.xy)/iResolution.y;

    vec2 z = c;

    float ar = 0.; // average of reciprocals
    float i;
    for (i = 0.; i < 1000.; i++) {
        ar += 1./length(z);
        z = vec2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y) + c;
    }
    ar = ar / i;

    fragColor = vec4(vec3(2. / ar), 1.0);
}

It does produce a gradient in every bulb, but it is clear that it's not usable as a distance estimator by itself because values in smaller bulbs have inconsistent magnitude (brightness) compared to bigger bulbs. So it's clear that a parameter is missing but I don't know what it is.

I don't require a perfect solution nor one that converges into a perfect solution like in this image.

Something that at least guarantees a lower bound is plenty.

Sleight

Answer 1

My bet is that 1./length(z) is hitting the precision of float try to use double and dvec2 instead of float,vec2 if it makes any difference. If it does then I would ignore too small values of length(z).

Alternatively you can render just the boundary into texture in one pass and then just scan neighbors in all directions until boundary found returning the ray length. (may require some morphology operators before safe use)

This can be speed up with another pass where you "flood" fill incrementing distance into texture until its filled (better done on CPU side as you need R/W access to the same texture) its similar to A* filling however your precision will be limited by texture resolution.

If I ported my mandlebrot from link above to your computation ported to doubles and added the threshold:

// Fragment
#version 450 core
uniform dvec2 p0=vec2(0.0,0.0);     // mouse position <-1,+1>
uniform double zoom=1.000;          // zoom [-]
uniform int  n=100;                 // iterations [-]
in smooth vec2 p32;
out vec4 col;

vec3 spectral_color(float l)        // RGB <0,1> <- lambda l <400,700> [nm]
    {
    float t;  vec3 c=vec3(0.0,0.0,0.0);
         if ((l>=400.0)&&(l<410.0)) { t=(l-400.0)/(410.0-400.0); c.r=    +(0.33*t)-(0.20*t*t); }
    else if ((l>=410.0)&&(l<475.0)) { t=(l-410.0)/(475.0-410.0); c.r=0.14         -(0.13*t*t); }
    else if ((l>=545.0)&&(l<595.0)) { t=(l-545.0)/(595.0-545.0); c.r=    +(1.98*t)-(     t*t); }
    else if ((l>=595.0)&&(l<650.0)) { t=(l-595.0)/(650.0-595.0); c.r=0.98+(0.06*t)-(0.40*t*t); }
    else if ((l>=650.0)&&(l<700.0)) { t=(l-650.0)/(700.0-650.0); c.r=0.65-(0.84*t)+(0.20*t*t); }
         if ((l>=415.0)&&(l<475.0)) { t=(l-415.0)/(475.0-415.0); c.g=             +(0.80*t*t); }
    else if ((l>=475.0)&&(l<590.0)) { t=(l-475.0)/(590.0-475.0); c.g=0.8 +(0.76*t)-(0.80*t*t); }
    else if ((l>=585.0)&&(l<639.0)) { t=(l-585.0)/(639.0-585.0); c.g=0.84-(0.84*t)           ; }
         if ((l>=400.0)&&(l<475.0)) { t=(l-400.0)/(475.0-400.0); c.b=    +(2.20*t)-(1.50*t*t); }
    else if ((l>=475.0)&&(l<560.0)) { t=(l-475.0)/(560.0-475.0); c.b=0.7 -(     t)+(0.30*t*t); }
    return c;
    }

void main()
    {
    int i,j;
    dvec2 pp,p;
    double x,y,q,xx,yy,mu,cx,cy;
    p=dvec2(p32);

    pp=(p/zoom)-p0;         // y (-1.0, 1.0)
    pp.x-=0.5;              // x (-1.5, 0.5)
    cx=pp.x;                // normal
    cy=pp.y;
/*
    // single pass mandelbrot integer escape
    for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n)&&(xx+yy<4.0);i++)
        {
        q=xx-yy+cx;
        y=(2.0*x*y)+cy;
        x=q;
        xx=x*x;
        yy=y*y;
        }
    float f=float(i)/float(n);
    f=pow(f,0.2);
    col=vec4(spectral_color(400.0+(300.0*f)),1.0);
*/
    // distance to boundary
    double ar=0.0,aa,nn=0.0;              // *** this is what I added
    for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n)&&(xx+yy<4.0);i++)
        {
        aa=length(dvec2(x,y));            // *** this is what I added
        if (aa>1e-3){ ar+=1.0/aa; nn++; } // *** this is what I added
        q=xx-yy+cx;
        y=(2.0*x*y)+cy;
        x=q;
        xx=x*x;
        yy=y*y;
        }
    ar=ar/nn;                             // *** this is what I added
    col=vec4(vec3(1.0-(2.0/ar)),1.0);     // *** this is what I added
    }

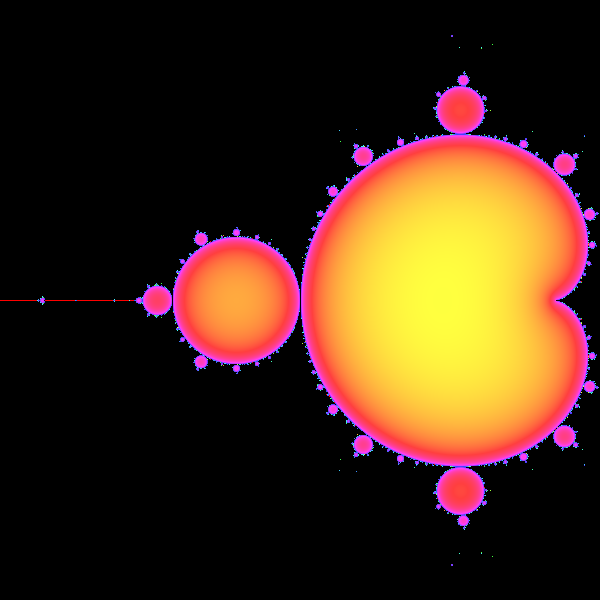
I got these outputs:

Just look for // *** this is what I added comment in the code that is what is added to the standard mandelbrot rendering to render distance instead. ps my (x,y) is your z and (cx,cy) is your c

anyway the distance is still highly nonlinear and depends on the position

[Edit1] non-isotropic scale

The black dot is the thresholds size you can lover it to 1e-20 ... Now I added level lines to show the distribution of distance scale (as I did not know how non isotropic and non linear it is...) here the output:

And coloring part of fragment (after the for loop):

ar=1.0-(2.0*nn/ar);
aa=10.0*ar; // 10 level lines per unit
aa-=floor(aa);
if (abs(aa)<0.05) col=vec4(0.0,1.0,0.0,1.0); // width and color of level line
 else             col=vec4(ar,ar,ar,1.0);

As you can see its not very parallel to border but still locally "constant" (the level lines are equidistant to each in local feature of fractal) so if gradient (derivate) used the result will be just very rough estimate (but should work). If that is enough what you should do is:

1. compute non linear distance for queried position and few point d distant to it in "all" directions.

2. pick that neighbor that has bigest change in distance to original point

3. rescale the estimated distances so their substraction will give you d. then use the first distance rescaled as output.

When put to fragment code (using 8-neighbors):

// Fragment
#version 450 core
uniform dvec2 p0=vec2(0.0,0.0);     // mouse position <-1,+1>
uniform double zoom=1.000;          // zoom [-]
uniform int  n=100;                 // iterations [-]
in smooth vec2 p32;
out vec4 col;

double mandelbrot_distance(double cx,double cy)
    {
    // distance to boundary
    int i,j;
    double x,y,q,xx,yy,ar=0.0,aa,nn=0.0;
    for (x=0.0,y=0.0,xx=0.0,yy=0.0,i=0;(i<n)&&(xx+yy<4.0);i++)
        {
        aa=length(dvec2(x,y));
        if (aa>1e-20){ ar+=1.0/aa; nn++; }
        q=xx-yy+cx;
        y=(2.0*x*y)+cy;
        x=q;
        xx=x*x;
        yy=y*y;
        }
    return 1.0-(2.0*nn/ar);
    }
void main()
    {
    dvec2 pp,p;
    double cx,cy,d,dd,d0,d1,e;
    p=dvec2(p32);

    pp=(p/zoom)-p0;         // y (-1.0, 1.0)
    pp.x-=0.5;              // x (-1.5, 0.5)
    cx=pp.x;                // normal
    cy=pp.y;
    d =0.01/zoom;           // normalization distance
    e =sqrt(0.5)*d;
    dd=mandelbrot_distance(cx,cy);
    if (dd>0.0)
        {
        d0=mandelbrot_distance(cx-d,cy  ); if (d0>0.0)  d0=abs(d0-dd);
        d1=mandelbrot_distance(cx+d,cy  ); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx  ,cy-d); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx  ,cy+d); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx-e,cy-e); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx+e,cy-e); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx-e,cy+e); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        d1=mandelbrot_distance(cx+e,cy+e); if (d1>0.0){ d1=abs(d1-dd); if (d0<d1) d0=d1; }
        dd*=d/d0;
        }
    dd*=zoom; // just for visualization of small details real distance should not be scaled by this
    col=vec4(dd,dd,dd,1.0);
    }

here the result:

As you can see its now much more correct (but very close to border is inaccurate due to non isotropy mentioned above). The 8 neighbors produces the 8 diagonal like lines pattern in the circular blobs. If you want to get rid of them you should scan whole circle around the position instead of just 8 points.

Also there are still some white dots (they are not accuracy related) I think they are cases when the selected d distant neighbor is across the mandelbrot edge in different blob than original. That could be filtered out ... (you know d/2 distance in the same direction should be half if not you are in different blob)

However even 8 neighbors are pretty slow. So I for more accuracy I would recommend to go for the 2 pass "ray casting" method instead.

Varnado

I was able to reproduce your last picture simply by adding the "1.0-" to the final color and the threshold only seems to add those black spots in every bulb, so i don't think increasing float precision helps unfortunately. I'm thinking however that if there was a way to make the gradients end at the boundary with first derivative equal zero, it would be possible to walk the slope until first derivative becomes close enough to zero. Any ideas? – Sleight

@Sleight I added edit1 with normalized output and much smaller threshold to get rid of the black dots in usable zooms. – Varnado