Vectorized Numpy (1d) version of itertools.combinations

Question

Im trying to accomplish a Vectoriced Numpy version of itertools.combinations, that I futher can decorate with @jit (Numba) - To make it even faster. (I am not sure if this even can be done)

The dataset im working on is a 1d - np.array, the goal is to get combinations with set of 3.

x = np.array([1,2,3,4,5])

set(combinations(x, 3))

Result:

{(1, 2, 3),
 (1, 2, 4),
 (1, 2, 5),
 (1, 3, 4),
 (1, 3, 5),
 (1, 4, 5),
 (2, 3, 4),
 (2, 3, 5),
 (2, 4, 5),
 (3, 4, 5)}

I have been searching stack & other resources, I did find quite alot info on this topic, but not any usefull info in regards to my usecase.

N-D version of itertools.combinations in numpy

This thread indicates that it probably are quite hard to get anything faster than itertools.combinations:

numba-safe version of itertools.combinations?

---

I was asked to specify the usecase a bit more:

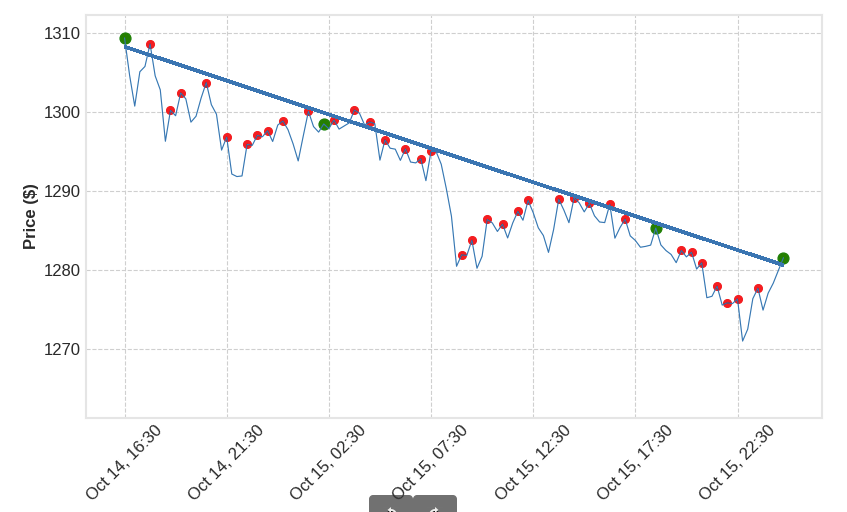
1. I have a price data np.array price= ([100,101,102,103,104,105 etc..])

2. I use scipy.signal.argrelmax to find all peaks in the array. (red dots in above pic.)

3. I will now need to get all combinations of the peaks.

4. Then I will run simple linear regression over all combination, and look for a certain r_val treshold, to verify a trendline.(green dot in above picture)

(The combination of 3 is because then I know the trendline had 3 touches. On illustration I have posted it is 4 touches, so I work with both 3 or 4 touches.)

(futhermore I use integrals above / below trendline to filter)

I do not need the combi func. to return a set of tuples, the simple linear regression algo I have written, is optimized to numpy.

Jaquelinejaquelyn

Can you tell us more about your use-case? Do you really need the output to be a set of tuple? Creating such data structure is not efficient since every tuple needs to be allocated separately, then hashed and then stored in the CPython dynamic set data structure. Numba does not support such data structure efficiently (but typed sets and typed tuples instead) because they are inherently dynamic. Is the input array small or big? Is the number of item in tuples always 3. Such details are critical to write a fast code. Generic high-level codes are (nearly) never efficient. – Ethnic

@JérômeRichard great question ! - I did add more info to my question. Ask if you need even more info. – Jaquelinejaquelyn

Answer 1

itertools.combinations is sub-optimal in CPython since it has to call a C function for each combination and also because it has to create a new tuple. Calling C functions and allocating objects is a bit expensive in CPython. Additionally, the code is generic while it can be specialized for the case where one want to generate combinations of triplets or quadruplets like in your case. Computing the set is certainly not needed since the combination are ensured to be unique and sorted in the lexical order if the input x is composed of sorted unique items too. A binary search can be used to find if an array is a permutation of another. In fact, in this case, one can just sort the arrays and compare them. The Numba function can generate all the combinations in a Numpy array. Lets first write an optimized generic function:

import numba as nb
import numpy as np

@nb.njit('(int64, int64)')
def combCount(n, r):
    if r < 0:
        return 0
    res = 1
    if r > n - r:
        r = n - r
    for i in range(r):
        res *= (n - i)
        res //= (i + 1)
    return res

@nb.njit(inline='always')
def genComb_generic(arr, r):
    n = arr.size
    out = np.empty((combCount(n, r), r), dtype=arr.dtype)
    idx = np.empty(r, dtype=np.int32)

    for i in range(r):
        idx[i] = i

    i = r - 1

    cur = 0
    while idx[0] < n - r + 1:
        while i > 0 and idx[i] == n - r + i:
            i -= 1
        for j in range(r):
            out[cur, j] = arr[idx[j]]
        cur += 1
        idx[i] += 1
        while i < r - 1:
            idx[i + 1] = idx[i] + 1
            i += 1
    return out

@nb.njit
def genComb_x3(arr):
    return genComb_generic(arr, 3)

@nb.njit
def genComb_x4(arr):
    return genComb_generic(arr, 4)

x = np.array([1,2,3,4,5])
genComb_x3(x) # generate triplets based on `x`

genComb_generic is fast, especially when the output is big, but it can be made faster when r is known. Here is a specific case where r=3 (triplets):

@nb.njit
def genComb_x3(arr):
    n = arr.size
    nComb = combCount(n, 3)
    out = np.empty((nComb, 3), dtype=arr.dtype)
    a, b, c = 0, 1, 2
    arr_a = arr[a]
    arr_b = arr[b]
    for cur in range(nComb):
        out[cur, 0] = arr_a
        out[cur, 1] = arr_b
        out[cur, 2] = arr[c]
        if c < n - 1:
            c += 1
        else:
            if b < n - 2:
                b, c = b + 1, b + 2
                arr_b = arr[b]
            else:
                a, b, c = a + 1, a + 2, a + 3
                arr_a = arr[a]
                arr_b = arr[b]
    return out

This last implementation is extremely fast compared to itertools when the output is relatively big. When x.size is 30, it is about 68 times faster than itertools. When x.size is 5, it is only about 2 times faster. This is because calling a Numba function from CPython as a significant overhead (like for Numpy), not to mention the time to allocate the output. This overhead is about 800 ns on my machine (i5-9600KF). You can reduce a lot the overhead by calling such function from another Numba function and preallocate the output if possible. In the end, the Numba function should be about 80 time faster than the itertool implementation in this case.

If you plan to generate a lot of combination, then it should be better to compute them on the fly rather than generating a huge array (since the RAM tends to be slow). This should be even faster.

Jarib

I will implement it monday, and give you the stats. - I'm learning a lot from your answer! thanks. – Jaquelinejaquelyn

It works like a charm - And yes, it is quite faster than Iter.comb in my usecase!. – Jaquelinejaquelyn