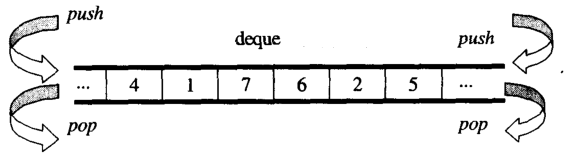
From overview, you can think deque as a double-ended queue
![deque overview]()
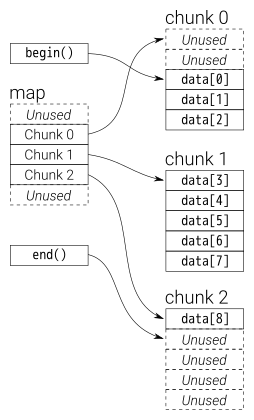
The datas in deque are stored by chuncks of fixed size vector, which are
pointered by a map(which is also a chunk of vector, but its size may change)
![deque internal structure]()
The main part code of the deque iterator is as below:
/*
buff_size is the length of the chunk
*/
template <class T, size_t buff_size>
struct __deque_iterator{
typedef __deque_iterator<T, buff_size> iterator;
typedef T** map_pointer;
// pointer to the chunk
T* cur;
T* first; // the begin of the chunk
T* last; // the end of the chunk
//because the pointer may skip to other chunk
//so this pointer to the map
map_pointer node; // pointer to the map
}
The main part code of the deque is as below:
/*
buff_size is the length of the chunk
*/
template<typename T, size_t buff_size = 0>
class deque{
public:
typedef T value_type;
typedef T& reference;
typedef T* pointer;
typedef __deque_iterator<T, buff_size> iterator;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
protected:
typedef pointer* map_pointer;
// allocate memory for the chunk
typedef allocator<value_type> dataAllocator;
// allocate memory for map
typedef allocator<pointer> mapAllocator;
private:
//data members
iterator start;
iterator finish;
map_pointer map;
size_type map_size;
}
Below i will give you the core code of deque, mainly about three parts:
iterator
How to construct a deque
1. iterator(__deque_iterator)
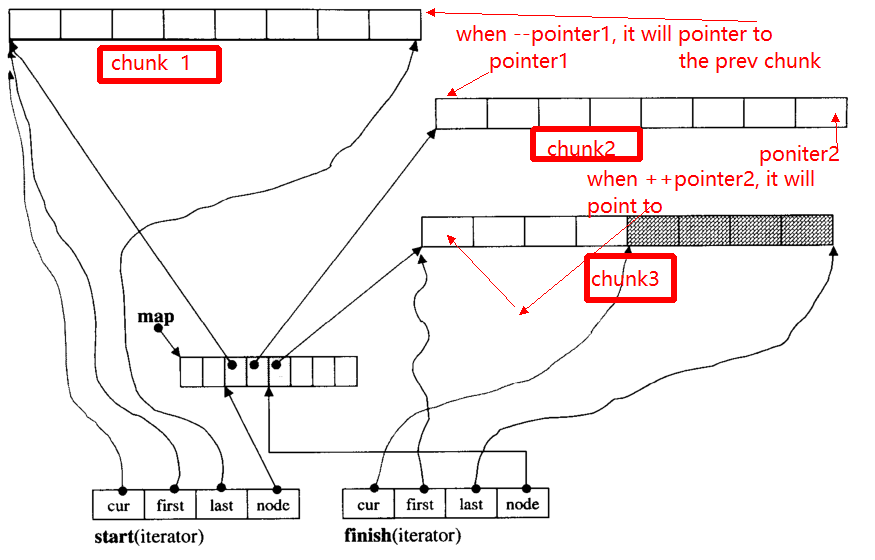
The main problem of iterator is, when ++, -- iterator, it may skip to other chunk(if it pointer to edge of chunk). For example, there are three data chunks: chunk 1,chunk 2,chunk 3.
The pointer1 pointers to the begin of chunk 2, when operator --pointer it will pointer to the end of chunk 1, so as to the pointer2.
![enter image description here]()
Below I will give the main function of __deque_iterator:
Firstly, skip to any chunk:
void set_node(map_pointer new_node){
node = new_node;
first = *new_node;
last = first + chunk_size();
}
Note that, the chunk_size() function which compute the chunk size, you can think of it returns 8 for simplify here.
operator* get the data in the chunk
reference operator*()const{
return *cur;
}
operator++, --
// prefix forms of increment
self& operator++(){
++cur;
if (cur == last){ //if it reach the end of the chunk
set_node(node + 1);//skip to the next chunk
cur = first;
}
return *this;
}
// postfix forms of increment
self operator++(int){
self tmp = *this;
++*this;//invoke prefix ++
return tmp;
}
self& operator--(){
if(cur == first){ // if it pointer to the begin of the chunk
set_node(node - 1);//skip to the prev chunk
cur = last;
}
--cur;
return *this;
}
self operator--(int){
self tmp = *this;
--*this;
return tmp;
}
iterator skip n steps / random access
self& operator+=(difference_type n){ // n can be postive or negative
difference_type offset = n + (cur - first);
if(offset >=0 && offset < difference_type(buffer_size())){
// in the same chunk
cur += n;
}else{//not in the same chunk
difference_type node_offset;
if (offset > 0){
node_offset = offset / difference_type(chunk_size());
}else{
node_offset = -((-offset - 1) / difference_type(chunk_size())) - 1 ;
}
// skip to the new chunk
set_node(node + node_offset);
// set new cur
cur = first + (offset - node_offset * chunk_size());
}
return *this;
}
// skip n steps
self operator+(difference_type n)const{
self tmp = *this;
return tmp+= n; //reuse operator +=
}
self& operator-=(difference_type n){
return *this += -n; //reuse operator +=
}
self operator-(difference_type n)const{
self tmp = *this;
return tmp -= n; //reuse operator +=
}
// random access (iterator can skip n steps)
// invoke operator + ,operator *
reference operator[](difference_type n)const{
return *(*this + n);
}
2. How to construct a deque
common function of deque
iterator begin(){return start;}
iterator end(){return finish;}
reference front(){
//invoke __deque_iterator operator*
// return start's member *cur
return *start;
}
reference back(){
// cna't use *finish
iterator tmp = finish;
--tmp;
return *tmp; //return finish's *cur
}
reference operator[](size_type n){
//random access, use __deque_iterator operator[]
return start[n];
}
template<typename T, size_t buff_size>
deque<T, buff_size>::deque(size_t n, const value_type& value){
fill_initialize(n, value);
}
template<typename T, size_t buff_size>
void deque<T, buff_size>::fill_initialize(size_t n, const value_type& value){
// allocate memory for map and chunk
// initialize pointer
create_map_and_nodes(n);
// initialize value for the chunks
for (map_pointer cur = start.node; cur < finish.node; ++cur) {
initialized_fill_n(*cur, chunk_size(), value);
}
// the end chunk may have space node, which don't need have initialize value
initialized_fill_n(finish.first, finish.cur - finish.first, value);
}
template<typename T, size_t buff_size>
void deque<T, buff_size>::create_map_and_nodes(size_t num_elements){
// the needed map node = (elements nums / chunk length) + 1
size_type num_nodes = num_elements / chunk_size() + 1;
// map node num。min num is 8 ,max num is "needed size + 2"
map_size = std::max(8, num_nodes + 2);
// allocate map array
map = mapAllocator::allocate(map_size);
// tmp_start,tmp_finish poniters to the center range of map
map_pointer tmp_start = map + (map_size - num_nodes) / 2;
map_pointer tmp_finish = tmp_start + num_nodes - 1;
// allocate memory for the chunk pointered by map node
for (map_pointer cur = tmp_start; cur <= tmp_finish; ++cur) {
*cur = dataAllocator::allocate(chunk_size());
}
// set start and end iterator
start.set_node(tmp_start);
start.cur = start.first;
finish.set_node(tmp_finish);
finish.cur = finish.first + num_elements % chunk_size();
}
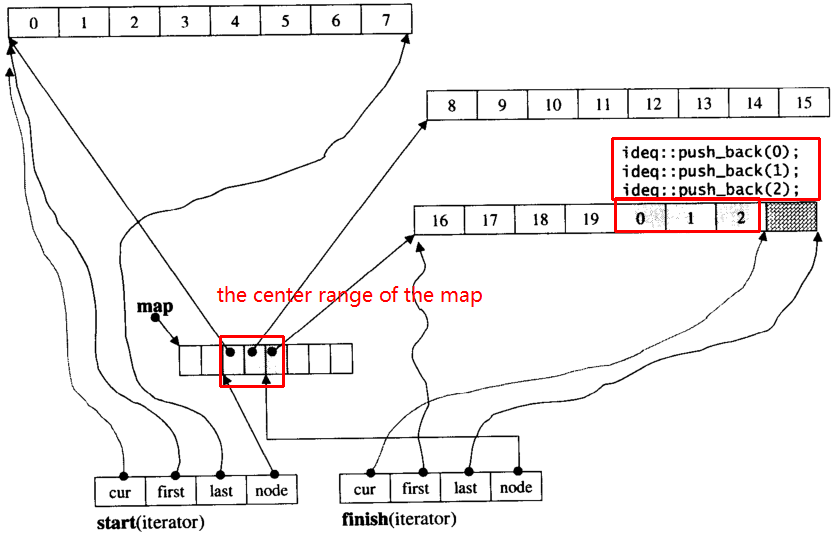
Let's assume i_deque has 20 int elements 0~19 whose chunk size is 8, and now push_back 3 elements (0, 1, 2) to i_deque:
i_deque.push_back(0);
i_deque.push_back(1);
i_deque.push_back(2);
It's internal structure like below:
![enter image description here]()
Then push_back again, it will invoke allocate new chunk:
push_back(3)
![enter image description here]()
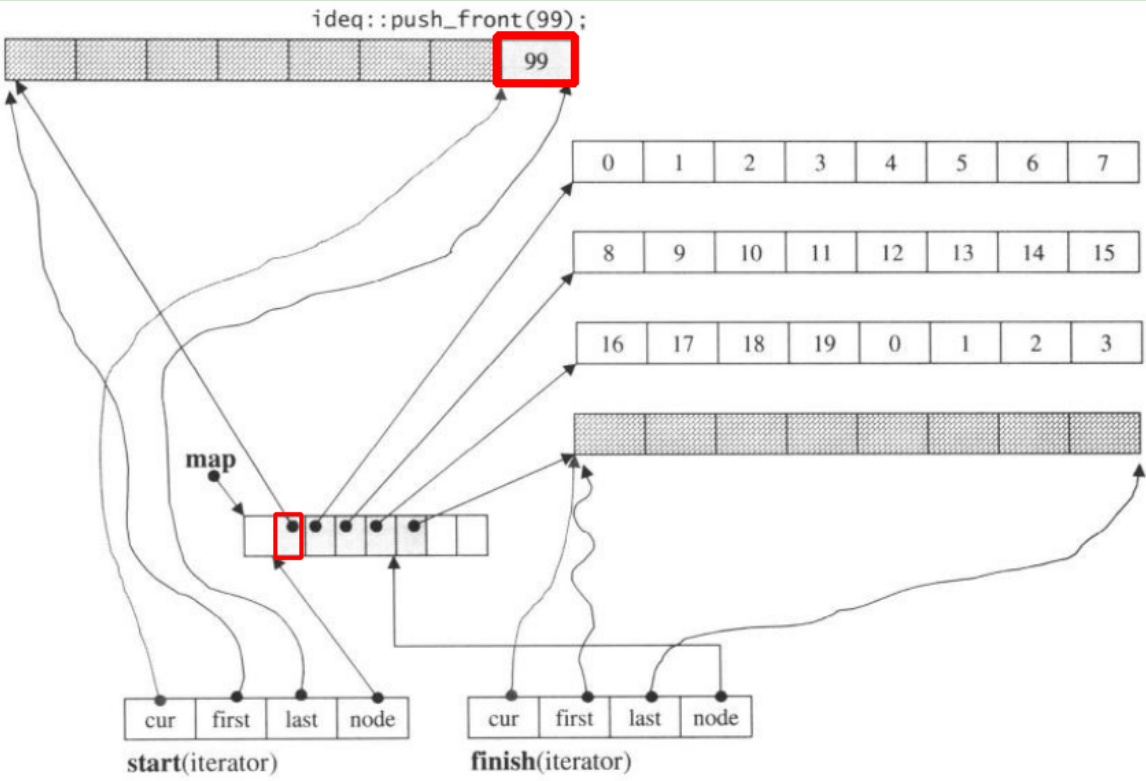
If we push_front, it will allocate new chunk before the prev start
![enter image description here]()
Note when push_back element into deque, if all the maps and chunks are filled, it will cause allocate new map, and adjust chunks.But the above code may be enough for you to understand deque.



dequestands for double ended queue, though obviously the stringent requirement of O(1) access to middle elements is particular to C++ – Subcontinent