Remove duplicate dict in list in Python

Question

I have a list of dicts, and I'd like to remove the dicts with identical key and value pairs.

For this list: [{'a': 123}, {'b': 123}, {'a': 123}]

I'd like to return this: [{'a': 123}, {'b': 123}]

Another example:

For this list: [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]

I'd like to return this: [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

Dc

Can you tell us more about the actual problem you're trying to solve? This seems like an odd problem to have. – Recording

I am combining a few lists of dicts and there are duplicates. So I need to remove those duplicates. – Dc

I found a solution in #480714 in an answer without the usage of set() – Hallo

@Recording I encountered this problem in real life with a large ETL script that queues data for upload as a list of dicts. Sometimes multiple records from Scope A will bring in the same records from Scope B, but no need to upload redundant output to the external system. – Liger

https://mcmap.net/q/108003/-remove-duplicate-dict-in-list-in-python use this answer if you are looking for fastest way – Supersede

Answer 1

Try this:

[dict(t) for t in {tuple(d.items()) for d in l}]

The strategy is to convert the list of dictionaries to a list of tuples where the tuples contain the items of the dictionary. Since the tuples can be hashed, you can remove duplicates using set (using a set comprehension here, older python alternative would be set(tuple(d.items()) for d in l)) and, after that, re-create the dictionaries from tuples with dict.

where:

• l is the original list
• d is one of the dictionaries in the list
• t is one of the tuples created from a dictionary

Edit: If you want to preserve ordering, the one-liner above won't work since set won't do that. However, with a few lines of code, you can also do that:

l = [{'a': 123, 'b': 1234},
        {'a': 3222, 'b': 1234},
        {'a': 123, 'b': 1234}]

seen = set()
new_l = []
for d in l:
    t = tuple(d.items())
    if t not in seen:
        seen.add(t)
        new_l.append(d)

print new_l

Example output:

[{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

Note: As pointed out by @alexis it might happen that two dictionaries with the same keys and values, don't result in the same tuple. That could happen if they go through a different adding/removing keys history. If that's the case for your problem, then consider sorting d.items() as he suggests.

Kennel

Nice solution but it has a bug: d.items() is not guaranteed to return elements in a particular order. You should do tuple(sorted(d.items())) to ensure you don't get different tuples for the same key-value pairs. – Algar

@Algar I made a few tests and you are indeed right. If a lot of keys are added in between and removed later, then that could be the case. Thanks a lot for your comment. – Kennel

Cool. I added the fix to your answer for the benefit of future readers who might not read the whole conversation. – Algar

Doesn't need "a lot of keys" to fail, already fails [{'a': 1, 'i': 2}, {'i': 2, 'a': 1}]. – Awe

Note, this will not work if you load in that list of dicts from a the json module as I did – Schoolmate

I can't seem to make this work for me and I imported my data from the json module – Fruitarian

This will throw an error if you have an OrderedDict as a value – Darceydarci

This is a valid solution in this case, but won't work in case of nested dictionaries – Haggadah

It says "TypeError: unhashable type: 'list'" for the step "if t not in seen:" – Agglutinate

@Kennel Is there a way to preserve dict with most keys. For example "a" key is the same for two dicts, but one of them have more keys ? – Muddy

Very pythonic but difficult to read – Aphesis

Answer 2

Another one-liner based on list comprehensions:

>>> d = [{'a': 123}, {'b': 123}, {'a': 123}]
>>> [i for n, i in enumerate(d) if i not in d[n + 1:]]
[{'b': 123}, {'a': 123}]

Here since we can use dict comparison, we only keep the elements that are not in the rest of the initial list (this notion is only accessible through the index n, hence the use of enumerate).

Fettling

This also works for a list of dictionaries which consist of lists as compared the the first answer – Mahalia

this also works when you may have an unhashable type as a value in your dictionaries, unlike the top answer. – Shirlshirlee

here, purpose is to remove duplicate values, not key, see this answer's code – Blab

This is very inefficient code. if i not in d[n + 1:] iterates over the entire list of dicts (from n but that just halves the total number of operations) and you're doing that check for every element in your dictionary so this this code is O(n^2) time complexity – Fleshings

doesn't work for dictionaries with dictionaries as values – Efrem

Works for unhashable types: lists as values in a dictionary from the top list of dictionaries. – Alidaalidade

Answer 3

If using a third-party package would be okay then you could use iteration_utilities.unique_everseen:

>>> from iteration_utilities import unique_everseen
>>> l = [{'a': 123}, {'b': 123}, {'a': 123}]
>>> list(unique_everseen(l))
[{'a': 123}, {'b': 123}]

It preserves the order of the original list and ut can also handle unhashable items like dictionaries by falling back on a slower algorithm (O(n*m) where n are the elements in the original list and m the unique elements in the original list instead of O(n)). In case both keys and values are hashable you can use the key argument of that function to create hashable items for the "uniqueness-test" (so that it works in O(n)).

In the case of a dictionary (which compares independent of order) you need to map it to another data-structure that compares like that, for example frozenset:

>>> list(unique_everseen(l, key=lambda item: frozenset(item.items())))
[{'a': 123}, {'b': 123}]

Note that you shouldn't use a simple tuple approach (without sorting) because equal dictionaries don't necessarily have the same order (even in Python 3.7 where insertion order - not absolute order - is guaranteed):

>>> d1 = {1: 1, 9: 9}
>>> d2 = {9: 9, 1: 1}
>>> d1 == d2
True
>>> tuple(d1.items()) == tuple(d2.items())
False

And even sorting the tuple might not work if the keys aren't sortable:

>>> d3 = {1: 1, 'a': 'a'}
>>> tuple(sorted(d3.items()))
TypeError: '<' not supported between instances of 'str' and 'int'

Benchmark

I thought it might be useful to see how the performance of these approaches compares, so I did a small benchmark. The benchmark graphs are time vs. list-size based on a list containing no duplicates (that was chosen arbitrarily, the runtime doesn't change significantly if I add some or lots of duplicates). It's a log-log plot so the complete range is covered.

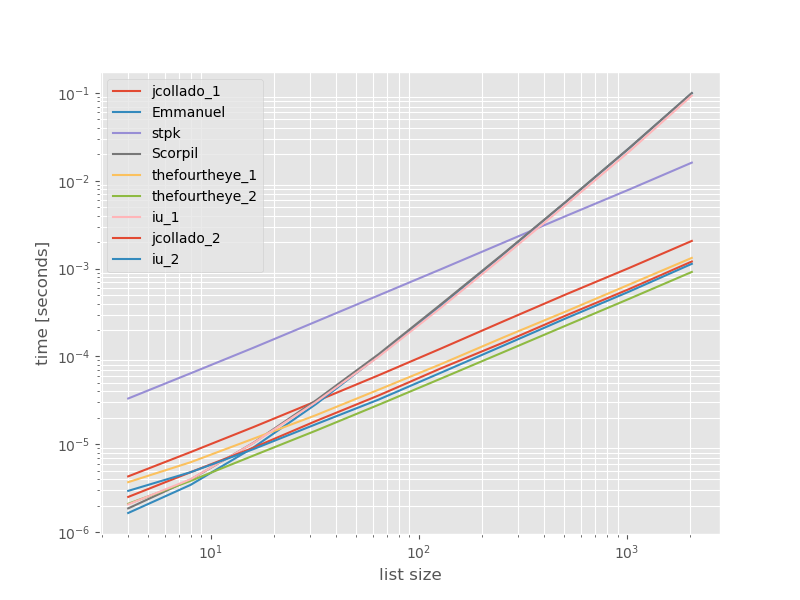
The absolute times:

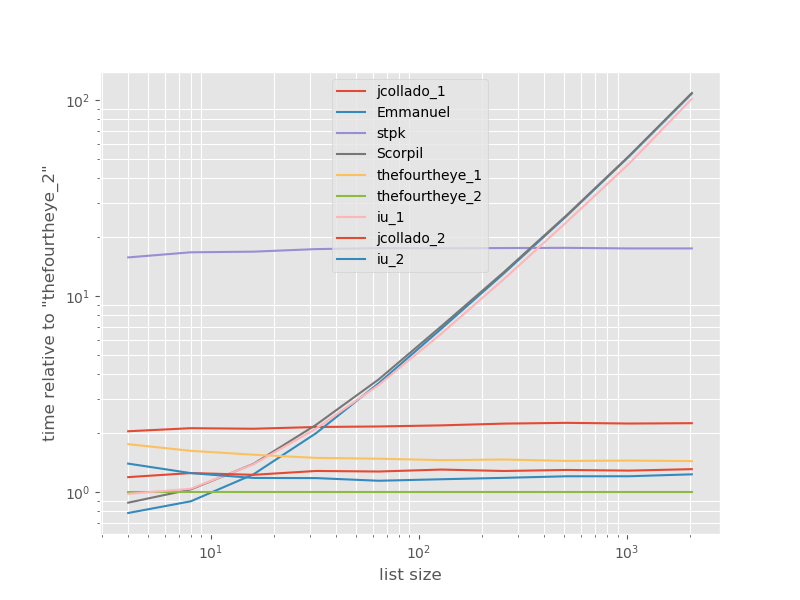
The timings relative to the fastest approach:

The second approach from thefourtheye is fastest here. The unique_everseen approach with the key function is on the second place, however it's the fastest approach that preserves order. The other approaches from jcollado and thefourtheye are almost as fast. The approach using unique_everseen without key and the solutions from Emmanuel and Scorpil are very slow for longer lists and behave much worse O(n*n) instead of O(n). stpks approach with json isn't O(n*n) but it's much slower than the similar O(n) approaches.

The code to reproduce the benchmarks:

from simple_benchmark import benchmark
import json
from collections import OrderedDict
from iteration_utilities import unique_everseen

def jcollado_1(l):
    return [dict(t) for t in {tuple(d.items()) for d in l}]

def jcollado_2(l):
    seen = set()
    new_l = []
    for d in l:
        t = tuple(d.items())
        if t not in seen:
            seen.add(t)
            new_l.append(d)
    return new_l

def Emmanuel(d):
    return [i for n, i in enumerate(d) if i not in d[n + 1:]]

def Scorpil(a):
    b = []
    for i in range(0, len(a)):
        if a[i] not in a[i+1:]:
            b.append(a[i])

def stpk(X):
    set_of_jsons = {json.dumps(d, sort_keys=True) for d in X}
    return [json.loads(t) for t in set_of_jsons]

def thefourtheye_1(data):
    return OrderedDict((frozenset(item.items()),item) for item in data).values()

def thefourtheye_2(data):
    return {frozenset(item.items()):item for item in data}.values()

def iu_1(l):
    return list(unique_everseen(l))

def iu_2(l):
    return list(unique_everseen(l, key=lambda inner_dict: frozenset(inner_dict.items())))

funcs = (jcollado_1, Emmanuel, stpk, Scorpil, thefourtheye_1, thefourtheye_2, iu_1, jcollado_2, iu_2)
arguments = {2**i: [{'a': j} for j in range(2**i)] for i in range(2, 12)}
b = benchmark(funcs, arguments, 'list size')

%matplotlib widget
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('ggplot')
mpl.rcParams['figure.figsize'] = '8, 6'

b.plot(relative_to=thefourtheye_2)

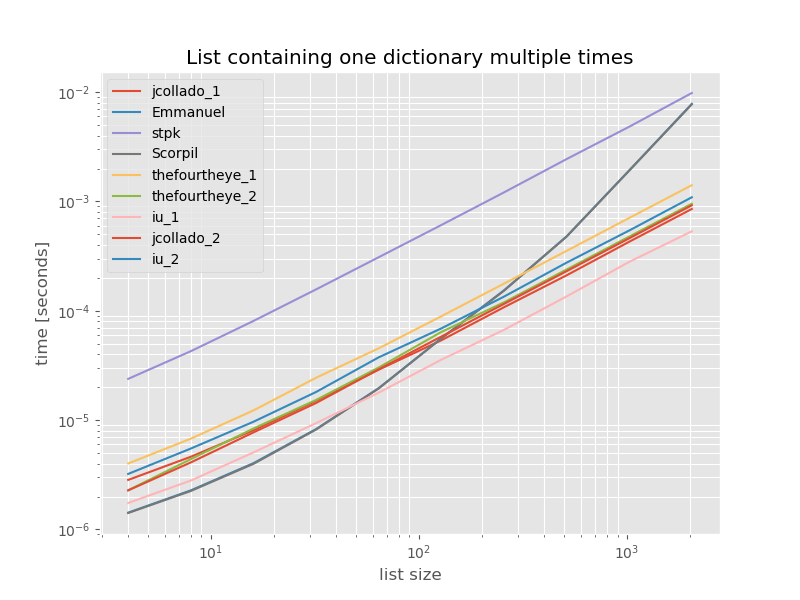
For completeness here is the timing for a list containing only duplicates:

# this is the only change for the benchmark
arguments = {2**i: [{'a': 1} for j in range(2**i)] for i in range(2, 12)}

The timings don't change significantly except for unique_everseen without key function, which in this case is the fastest solution. However that's just the best case (so not representative) for that function with unhashable values because it's runtime depends on the amount of unique values in the list: O(n*m) which in this case is just 1 and thus it runs in O(n).

---

Disclaimer: I'm the author of iteration_utilities.

Jotunheim

Can you share the Python version of the unique_everseen source code? GitHub only has .c versions. – Damle

@Damle The code is compiled to a Python C extension. There's not really a Python version. However the code is based on the recipe in docs.python.org/3/library/itertools.html#itertools-recipes (just a bit more optimized) – Jotunheim

Answer 4

Other answers would not work if you're operating on nested dictionaries such as deserialized JSON objects. For this case you could use:

import json
set_of_jsons = {json.dumps(d, sort_keys=True) for d in X}
X = [json.loads(t) for t in set_of_jsons]

Alviani

Great! the trick is that dict object cannot be directly added to a set, it needs to be converted to json object by dump(). – Mop

Answer 5

If you are using Pandas in your workflow, one option is to feed a list of dictionaries directly to the pd.DataFrame constructor. Then use drop_duplicates and to_dict methods for the required result.

import pandas as pd

d = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]

d_unique = pd.DataFrame(d).drop_duplicates().to_dict('records')

print(d_unique)

[{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

Sharecrop

For future googlers. You might also want to add astype(str) after pd.DataFrame() -> pd.DataFrame().astype(str). Otherwise you might receive a TypeError: unhashable type: 'dict' error. – Slating

That's a great solution, If you add details like how this method would perform compared with others mentioned answers in terms of performance. That would be great too. – Averyaveryl

Answer 6

If you want to preserve the Order, then you can do

from collections import OrderedDict
print OrderedDict((frozenset(item.items()),item) for item in data).values()
# [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

If the order doesn't matter, then you can do

print {frozenset(item.items()):item for item in data}.values()
# [{'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]

Pragmatic

Note: in python 3, your second approach gives a non-serializable dict_values output instead of a list. You have to cast the whole thing in a list again. list(frozen.....) – Generable

why this is not marked as correct answer? this method is faster and reduces time from 40 min to 1 min for me. thx – Supersede

//why this is not marked as correct answer// because the person who asked the question is the one who gets to decide ... if this is correct for your use, you can still up-vote this answer, even though you were not the one who originally asked the question – Shenika

Answer 7

Sometimes old-style loops are still useful. This code is little longer than jcollado's, but very easy to read:

a = [{'a': 123}, {'b': 123}, {'a': 123}]
b = []
for i in range(len(a)):
    if a[i] not in a[i+1:]:
        b.append(a[i])

Cumulus

The 0in range(0, len(a)) is not necessary. – Inspectorate

Answer 8

Not a universal answer, but if your list happens to be sorted by some key, like this:

l=[{'a': {'b': 31}, 't': 1},
   {'a': {'b': 31}, 't': 1},
 {'a': {'b': 145}, 't': 2},
 {'a': {'b': 25231}, 't': 2},
 {'a': {'b': 25231}, 't': 2}, 
 {'a': {'b': 25231}, 't': 2}, 
 {'a': {'b': 112}, 't': 3}]

then the solution is as simple as:

import itertools
result = [a[0] for a in itertools.groupby(l)]

Result:

[{'a': {'b': 31}, 't': 1},
{'a': {'b': 145}, 't': 2},
{'a': {'b': 25231}, 't': 2},
{'a': {'b': 112}, 't': 3}]

Works with nested dictionaries and (obviously) preserves order.

Ascites

This works even with a dictionary with a list in it. – Circumvallate

Answer 9

Input

input_list = [**{'a': 123, 'b': 1234}**, {'a': 3222, 'b': 1234}, **{'a': 123, 'b': 1234}**]

Output Required

>>> [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

Code

list = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]

empty_list = []

for item in list:
    if item not in empty_list:
        empty_list.append(item)

print("previous list = ",list)
print("Updated list = ",empty_list)

Output

>>> previous list = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]
>>> Updated list = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}]

Automatism

Answer 10

You can use a set, but you need to turn the dicts into a hashable type.

seq = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]
unique = set()
for d in seq:
    t = tuple(d.iteritems())
    unique.add(t)

Unique now equals

set([(('a', 3222), ('b', 1234)), (('a', 123), ('b', 1234))])

To get dicts back:

[dict(x) for x in unique]

Keeney

The order of d.iteritems() isn't guaranteed - so you may end up with 'duplicates' in unique. – Outsider

Answer 11

Not so short but easy to read:

list_of_data = [{'a': 123}, {'b': 123}, {'a': 123}]

list_of_data_uniq = []
for data in list_of_data:
    if data not in list_of_data_uniq:
        list_of_data_uniq.append(data)

Now, list list_of_data_uniq will have unique dicts.

Cabbage

Answer 12

Easiest way, convert each item in the list to string, since dictionary is not hashable. Then you can use set to remove the duplicates.

list_org = [{'a': 123}, {'b': 123}, {'a': 123}]
list_org_updated = [ str(item) for item in list_org]
print(list_org_updated)
["{'a': 123}", "{'b': 123}", "{'a': 123}"]
unique_set = set(list_org_updated)
print(unique_set)
{"{'b': 123}", "{'a': 123}"}

You can use the set, but if you do want a list, then add the following:

import ast
unique_list = [ast.literal_eval(item) for item in unique_set]
print(unique_list)
[{'b': 123}, {'a': 123}]

Ransome

Answer 13

Remove duplications by custom key:

def remove_duplications(arr, key):
    return list({key(x): x for x in arr}.values())

Devondevona

Answer 14

Here's a quick one-line solution with a doubly-nested list comprehension (based on @Emmanuel 's solution).

This uses a single key (for example, a) in each dict as the primary key, rather than checking if the entire dict matches

[i for n, i in enumerate(list_of_dicts) if i.get(primary_key) not in [y.get(primary_key) for y in list_of_dicts[n + 1:]]]

It's not what OP asked for, but it's what brought me to this thread, so I figured I'd post the solution I ended up with

Fabulous

Answer 15

A lot of good examples searching for duplicate values and keys, below is the way we filter out whole dictionary duplicate data in lists. Use dupKeys = [] if your source data is comprised of EXACT formatted dictionaries and looking for duplicates. Otherwise set dupKeys = to the key names of the data you want to not have duplicate entries of, can be 1 to n keys. It aint elegant, but works and is very flexible

import binascii

collected_sensor_data = [{"sensor_id":"nw-180","data":"XXXXXXX"},
                         {"sensor_id":"nw-163","data":"ZYZYZYY"},
                         {"sensor_id":"nw-180","data":"XXXXXXX"},
                         {"sensor_id":"nw-97", "data":"QQQQQZZ"}]

dupKeys = ["sensor_id", "data"]

def RemoveDuplicateDictData(collected_sensor_data, dupKeys):

    checkCRCs = []
    final_sensor_data = []
    
    if dupKeys == []:
        for sensor_read in collected_sensor_data:
            ck1 = binascii.crc32(str(sensor_read).encode('utf8'))
            if not ck1 in checkCRCs:
                final_sensor_data.append(sensor_read)
                checkCRCs.append(ck1)
    else:
        for sensor_read in collected_sensor_data:
            tmp = ""
            for k in dupKeys:
                tmp += str(sensor_read[k])

            ck1 = binascii.crc32(tmp.encode('utf8'))
            if not ck1 in checkCRCs:
                final_sensor_data.append(sensor_read)
                checkCRCs.append(ck1)
  
           
    return final_sensor_data    

 final_sensor_data = [{"sensor_id":"nw-180","data":"XXXXXXX"},
                      {"sensor_id":"nw-163","data":"ZYZYZYY"},
                      {"sensor_id":"nw-97", "data":"QQQQQZZ"}]
    

Sade

Answer 16

If you don't care about scale and crazy performance, simple func:

# Filters dicts with the same value in unique_key
# in: [{'k1': 1}, {'k1': 33}, {'k1': 1}]
# out: [{'k1': 1}, {'k1': 33}]
def remove_dup_dicts(list_of_dicts: list, unique_key) -> list:
    unique_values = list()
    unique_dicts = list()
    for obj in list_of_dicts:
        val = obj.get(unique_key)
        if val not in unique_values:
            unique_values.append(val)
            unique_dicts.append(obj)
    return unique_dicts

Cataplasm

Answer 17

If all values in dicts is hashable objects and order is important:

def list_no_duplicates(list_dicts):
    usage_dicts = set()
    for dictionary in list_dicts:
        dict_set = frozenset(dictionary.items())
        if dict_set not in usage_dicts:
            yield dictionary
            usage_dicts.add(dict_set)

example:

l = [{"key1": "value1"}, {"k1": "v1", "k2": "v2", "k3": "v3"}, {}, {}, {"key1": "value1"}, 
     {"key1": "value1"}, {"key2": "value2"}, {"k2": "v2", "k1": "v1", "k3": "v3"},]

print(list(list_no_duplicates(l)))
>>> [{'key1': 'value1'}, {'k1': 'v1', 'k2': 'v2', 'k3': 'v3'}, {}, {'key2': 'value2'}]

Effluvium

Answer 18

You can use list comprehension syntax to make it cleaner and more classy:

my_list = [{id:1, name:'test'}, {id:2, name:'test2'}, {id:1, name:'test'}]

my_list_unique = [i for n, i in enumerate(my_list) if i not in my_list[:n]]

# my_list_unique would be [{id:1, name:'test'}, {id:2, name:'test2'}]

Undergarment

Answer 19

Another clean way is by extending dict class and making it hashable:

class HashableDict(dict):
    def __hash__(self):
        return hash(tuple(sorted(self.items())))

Then, we can already use it to e.g. add to unique data structures such as set or keys of a dict:

>>> {{"exam": "ple"}, {"1": "2"}}  # Will fail as dict is mutable and can't be hashed.
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'dict'
>>> 
>>> {HashableDict({"exam": "ple"}), HashableDict({"1": "2"})}  # Will be successful due to the custom hasher.
{{'exam': 'ple'}, {'1': '2'}}

So from your expectations:

list1 = [{'a': 123}, {'b': 123}, {'a': 123}]
assert set(map(HashableDict, list1)) == set(map(HashableDict, [{'a': 123}, {'b': 123}]))

list2 = [{'a': 123, 'b': 1234}, {'a': 3222, 'b': 1234}, {'b': 1234, 'a': 123}]
assert set(map(HashableDict, list2)) == set(map(HashableDict, [{'a': 3222, 'b': 1234}, {'a': 123, 'b': 1234}]))

Nubble