Using scipy gaussian kernel density estimation to calculate CDF inverse

Question

The gaussian_kde function in scipy.stats has a function evaluate that can returns the value of the PDF of an input point. I'm trying to use gaussian_kde to estimate the inverse CDF. The motivation is for generating Monte Carlo realizations of some input data whose statistical distribution is numerically estimated using KDE. Is there a method bound to gaussian_kde that serves this purpose?

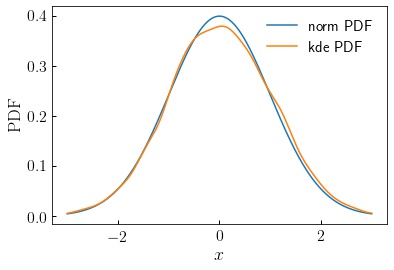
The example below shows how this should work for the case of a Gaussian distribution. First I show how to do the PDF calculation to set up the specific API I'm trying to achieve:

import numpy as np 
from scipy.stats import norm, gaussian_kde

npts_kde = int(5e3)
n = np.random.normal(loc=0, scale=1, size=npts_kde)
kde = gaussian_kde(n)

npts_sample = int(1e3)
x = np.linspace(-3, 3, npts_sample)
kde_pdf = kde.evaluate(x)
norm_pdf = norm.pdf(x)

Is there an analogously simple way to compute the inverse CDF? The norm function has a very handy isf function that does exactly this:

cdf_value = np.sort(np.random.rand(npts_sample))
cdf_inv = norm.isf(1 - cdf_value)

Does such a function exist for kde_gaussian? Or is it straightforward to construct such a function from the already implemented methods?

Charinile

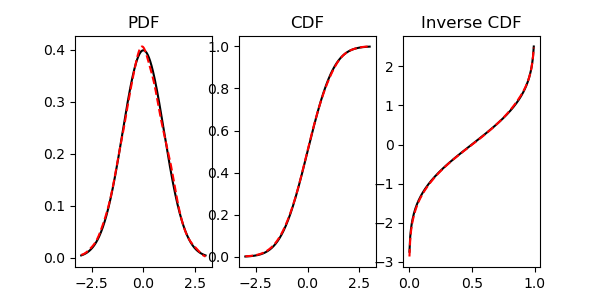
If your ultimate goal is resampling why not use the resample method? – Tobacco

My ultimate goal is not random resampling, but correlated resampling. If the resample method permitted me to pass in CDF values (the way that the isf method does), then my problem would be solved. But resample presumes I want to use a random uniform to generate the sample via the inverse CDF, which I do not. – Charinile

How about a root finder, then? Would that be too slow? – Tobacco

Hmm, not sure I understand. I guess you're suggesting I run a root-finder for a numerical integration of the PDF? – Charinile

I've never used this kde stuff, but the integrate_box_1d method sounds like almost the cdf to me, Maybe you can even put -inf for a boundary? And the cdf you can invert using a root finder - not the fastest, obviously. – Tobacco

Yes, this is a really good suggestion. My numerical integration of the PDF using scipy.integrate.quad is about 50x slower than integrate_box_1d. So this will actually be quite fast. If you write this up as a suggested answer, that will very likely be the accepted answer. Otherwise I'll write it up after making the explanation explicit and clear. Either way, thanks for the tip! – Charinile

Looks like I got scooped. Anyway, glad to have been of help. – Tobacco

Answer 1

The method integrate_box_1d can be used to compute the CDF, but it is not vectorized; you'll need to loop over points. If memory is not an issue, rewriting its source code (which is essentially just a call to special.ndtr) in vector form may speed things up.

from scipy.special import ndtr
stdev = np.sqrt(kde.covariance)[0, 0]
pde_cdf = ndtr(np.subtract.outer(x, n)).mean(axis=1)
plot(x, pde_cdf)

The plot of the inverse function would be plot(pde_cdf, x). If the goal is to compute the inverse function at a specific point, consider using the inverse of interpolating spline, interpolating the computed values of the CDF.

Culprit

I found I had to modify the pde_cdf line slightly: pde_cdf = ndtr(np.subtract.outer(x, n)/stdev).mean(axis=1). You'll see the division by the standard deviation in the source code you point to. Mathematically, I think this is required anyway. And if you are lucky enough to look at things like a normal distribution, this sort-of does ok. But without the stdev it really breaks if you are looking at anything not "normal". It is working here because the width of your gaussian is 1.0. – Greasy

Answer 2

The question has been answered in the other answers but it took me a while to wrap my mind around everything. Here is a complete example of the final solution:

import numpy as np 
from scipy import interpolate
from scipy.special import ndtr
import matplotlib.pyplot as plt
from scipy.stats import norm, gaussian_kde

# create kde
npts_kde = int(5e3)
n = np.random.normal(loc=0, scale=1, size=npts_kde)
kde = gaussian_kde(n)

# grid for plotting
npts_sample = int(1e3)
x = np.linspace(-3, 3, npts_sample)

# evaluate pdfs
kde_pdf = kde.evaluate(x)
norm_pdf = norm.pdf(x)

# cdf and inv cdf are available directly from scipy
norm_cdf = norm.cdf(x)
norm_inv = norm.ppf(x)

# estimate cdf
cdf = tuple(ndtr(np.ravel(item - kde.dataset) / kde.factor).mean()
            for item in x)

# estimate inv cdf
inversefunction = interpolate.interp1d(cdf, x, kind='cubic', bounds_error=False)

fig, ax = plt.subplots(1, 3, figsize=(6, 3))
ax[0].plot(x, norm_pdf, c='k')
ax[0].plot(x, kde_pdf, c='r', ls='--')
ax[0].set_title('PDF')
ax[1].plot(x, norm_cdf, c='k')
ax[1].plot(x, cdf, c='r', ls='--')
ax[1].set_title('CDF')
ax[2].plot(x, norm_inv, c='k')
ax[2].plot(x, inversefunction(x), c='r', ls='--')
ax[2].set_title("Inverse CDF")

Clearing

Answer 3

You can use some python tricks for fast and memory-effective estimation of the CDF (based on this answer):

    from scipy.special import ndtr
    cdf = tuple(ndtr(np.ravel(item - kde.dataset) / kde.factor).mean()
                for item in x)

It works as fast as this answer, but has linear (len(kde.dataset)) space complexity instead of the quadratic (actually, len(kde.dataset) * len(x)) one.

All you have to do next is to use inverse approximation, for instance, from statsmodels.

Housel