Using scipy.interpolate.splrep function

Question

I am trying to fit a cubic spline to a given set of points. My points are not ordered. I CANNOT sort or reorder the points, since I need that information.

But since the function scipy.interpolate.splrep works only on non-duplicate and monotonically increasing points I have defined a function that maps the x-coordinates to a monotonically increasing space.

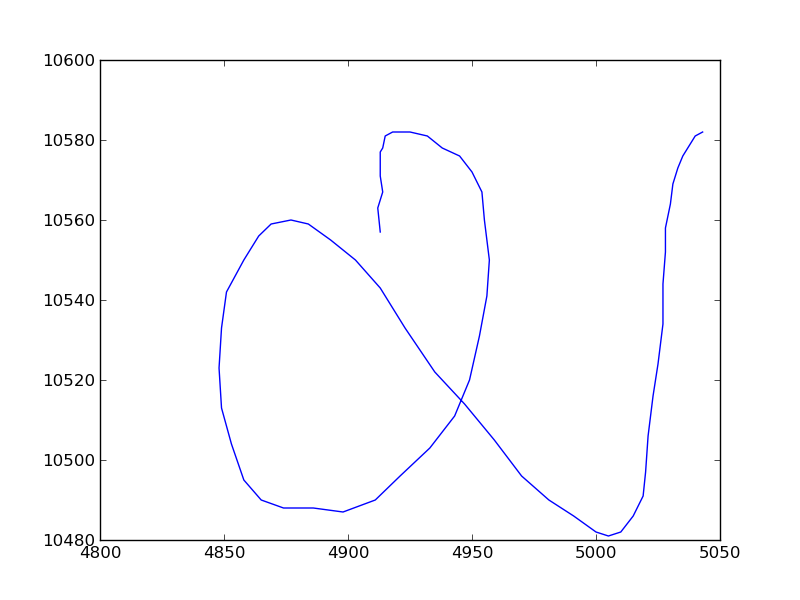
My old points are:

xpoints=[4913.0, 4912.0, 4914.0, 4913.0, 4913.0, 4913.0, 4914.0, 4915.0, 4918.0, 4921.0, 4925.0, 4932.0, 4938.0, 4945.0, 4950.0, 4954.0, 4955.0, 4957.0, 4956.0, 4953.0, 4949.0, 4943.0, 4933.0, 4921.0, 4911.0, 4898.0, 4886.0, 4874.0, 4865.0, 4858.0, 4853.0, 4849.0, 4848.0, 4849.0, 4851.0, 4858.0, 4864.0, 4869.0, 4877.0, 4884.0, 4893.0, 4903.0, 4913.0, 4923.0, 4935.0, 4947.0, 4959.0, 4970.0, 4981.0, 4991.0, 5000.0, 5005.0, 5010.0, 5015.0, 5019.0, 5020.0, 5021.0, 5023.0, 5025.0, 5027.0, 5027.0, 5028.0, 5028.0, 5030.0, 5031.0, 5033.0, 5035.0, 5037.0, 5040.0, 5043.0]

ypoints=[10557.0, 10563.0, 10567.0, 10571.0, 10575.0, 10577.0, 10578.0, 10581.0, 10582.0, 10582.0, 10582.0, 10581.0, 10578.0, 10576.0, 10572.0, 10567.0, 10560.0, 10550.0, 10541.0, 10531.0, 10520.0, 10511.0, 10503.0, 10496.0, 10490.0, 10487.0, 10488.0, 10488.0, 10490.0, 10495.0, 10504.0, 10513.0, 10523.0, 10533.0, 10542.0, 10550.0, 10556.0, 10559.0, 10560.0, 10559.0, 10555.0, 10550.0, 10543.0, 10533.0, 10522.0, 10514.0, 10505.0, 10496.0, 10490.0, 10486.0, 10482.0, 10481.0, 10482.0, 10486.0, 10491.0, 10497.0, 10506.0, 10516.0, 10524.0, 10534.0, 10544.0, 10552.0, 10558.0, 10564.0, 10569.0, 10573.0, 10576.0, 10578.0, 10581.0, 10582.0]

Plots:

The code for the mapping function and interpolation is:

xnew=[]
ynew=ypoints

for c3,i in enumerate(xpoints):
         if np.isfinite(np.log(i*pow(2,c3))):
                    xnew.append(np.log(i*pow(2,c3)))
         else:
                    if c==0: 
                        xnew.append(np.random.random_sample())
                    else:
                        xnew.append(xnew[c3-1]+np.random.random_sample())
xnew=np.asarray(xnew)
ynew=np.asarray(ynew)
constant1=10.0
nknots=len(xnew)/constant1
idx_knots = (np.arange(1,len(xnew)-1,(len(xnew)-2)/np.double(nknots))).astype('int')
knots = [xnew[i] for i in idx_knots]
knots = np.asarray(knots)
int_range=np.linspace(min(xnew),max(xnew),len(xnew))
tck = interpolate.splrep(xnew,ynew,k=3,task=-1,t=knots)
y1= interpolate.splev(int_range,tck,der=0)

The code is throwing an error at the function interpolate.splrep() for some set of points like the above one.

The error is: File "/home/neeraj/Desktop/koustav/res/BOS5/fit_spline3.py", line 58, in save_spline_f tck = interpolate.splrep(xnew,ynew,k=3,task=-1,t=knots) File "/usr/lib/python2.7/dist-packages/scipy/interpolate/fitpack.py", line 465, in splrep raise _iermessier(_iermess[ier][0]) ValueError: Error on input data

But for other set of points it works fine. For example for the following set of points.

xpoints=[1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1629.0, 1630.0, 1630.0, 1630.0, 1631.0, 1631.0, 1631.0, 1631.0, 1630.0, 1629.0, 1629.0, 1629.0, 1628.0, 1627.0, 1627.0, 1625.0, 1624.0, 1624.0, 1623.0, 1620.0, 1618.0, 1617.0, 1616.0, 1615.0, 1614.0, 1614.0, 1612.0, 1612.0, 1612.0, 1611.0, 1610.0, 1609.0, 1608.0, 1607.0, 1607.0, 1603.0, 1602.0, 1602.0, 1601.0, 1601.0, 1600.0, 1599.0, 1598.0]

ypoints=[10570.0, 10572.0, 10572.0, 10573.0, 10572.0, 10572.0, 10571.0, 10570.0, 10569.0, 10565.0, 10564.0, 10563.0, 10562.0, 10560.0, 10558.0, 10556.0, 10554.0, 10551.0, 10548.0, 10547.0, 10544.0, 10542.0, 10541.0, 10538.0, 10534.0, 10532.0, 10531.0, 10528.0, 10525.0, 10522.0, 10519.0, 10517.0, 10516.0, 10512.0, 10509.0, 10509.0, 10507.0, 10504.0, 10502.0, 10500.0, 10501.0, 10499.0, 10498.0, 10496.0, 10491.0, 10492.0, 10488.0, 10488.0, 10488.0, 10486.0, 10486.0, 10485.0, 10485.0, 10486.0, 10483.0, 10483.0, 10482.0, 10480.0]

Plots: Can anybody suggest what's happening ?? Thanks in advance......

Macule

With the code you have posted, ynew ends up being an empty array: you never append anything to that list. Hence the error. What exactly are you trying to fit the spline to? The points as odered? Or the points ordered in monotonically increasing x? Why can't you make an ordered copy of your data if that is what you need? – Edmonson

Sorry about the missing info. I have made ynew=ypoints. I am fitting the spline to (xnew,ynew). Since I cannot order the xpoints, I have mapped them to monotonically increasing points, xnew. After I have fitted the spline to (xnew,ynew) I am finding out a new set of points (y1,int_range). Here, int_range=np.linspace(min(xnew),max(xnew),len(xnew)) I have changed the code... Please have a look – Macule

You can use splrep(): #14244789 – Panpsychist

I have used that function only. Please go through my code once. splrep crashes giving that error I mentioned. I sense there is a bug in this function – Macule

Answer 1

Actually you do not have to define a new function yourself . It is like this trajectory interpolation very much :scipy: Interpolating trajectory(scipy: Interpolating trajectory )

And the answer is good for me, hope it can help you.

from scipy import interpolate as itp
mytck,myu=itp.splprep([xpoints,ypoints])
xnew,ynew= itp.splev(np.linspace(0,1,1000),mytck)
plot(xnew,ynew)

Mana

Answer 2

I believe that the purpose of the function you are using, splrep(), is to fit the y coordinate as a function of the x coordinate: y = f(x).

For splrep() to work as expected, your function must be single-valued. That is, you must be able to draw a vertical line on the graph anywhere and have it intersect the curve exactly once.

Instead, maybe you want to fit x and y separately to a third parameter t that increases monotonically.

x = f(t)
y = g(t)

There are two easy choices for t. The first is just the index of the point (0 for the first point, 1 for the second point, etc.). The second choice is a bit harder, the accumulated straight-line distance traveled from point to point. Then you would call slrep() separately for the x and y coordinates.

t = [0]
for i in range(1, len(x)):
  t[i] = t[i-1]+np.hypot(x[i]-x[i-1], y[i]-y[i-1])

Perhaps you instead want a bezier spline?

Faddish

Thanks for the answer. I tried to make this function monotonically increasing by using np.log(i*pow(2,c3)) .I tried using the first option you provided. The results were more or less same with the same errors. Can't we have duplicates for y values ? I have them. Is that a problem. I am not sure. But thanks (+1) for answering. – Macule

Answer 3

As mentioned in the documentation, it is very important for the X values to be unique in order to obtain sensible results. Which in your case is violated, so some correction on data might help.

Cantaloupe