How to simulate pink noise in R

Question

I know that white noise can be achieved by treating the output of rnorm() as a timeseries. Any suggestions on how to simulate pink noise?

Aleydis

Answer 1

Package tuneR has noise function which can generate a wave object that is either white or pink noise:

require(tuneR)
w <- noise(kind = c("white"))
p <- noise(kind = c("pink"))
par(mfrow=c(2,1))
plot(w,main="white noise")
plot(p,main="pink noise")

EDIT: I realized that the method above doesn't generate the vector (doh). Brutal way to convert it into the vector is to add the code below:

writeWave(p,"p.wav")#writes pink noise on your hard drive
require(audio)#loads `audio` package to use `load.wave` function
p.vec <- load.wave("path/to/p.wav")#this will load pink noise as a vector

Sutler

Isn't p@left enough to make a vector? (I can't check because of the CRAN failure.) – Disaffirm

Just out of interest, how would one write a generalized "color" noise function, i.e. suppress arbitrary regions of the bandwidth? That might be an enjoyable New Year's project for some R-nerd out there :-) – Deutsch

@Carl: You generate white gaussian noise, then run the samples through a filter to generate the desired power spectrum. Pink noise is defined as one with "1/f" power spectrum, so you need to design a filter with a "1/sqrt(f)" frequency response. Usually, you design a FIR (finite impulse response) filter approximating the desired response in some frequency band of interest. – Stonybroke

Answer 2

As said by @mbq, you can just use p@left to get the vector, instead of saving and reading the wav file. On the other hand, you could directly use the function generating the time serie in tuneR:

TK95 <- function(N, alpha = 1){ 
    f <- seq(from=0, to=pi, length.out=(N/2+1))[-c(1,(N/2+1))] # Fourier frequencies
    f_ <- 1 / f^alpha # Power law
    RW <- sqrt(0.5*f_) * rnorm(N/2-1) # for the real part
    IW <- sqrt(0.5*f_) * rnorm(N/2-1) # for the imaginary part
    fR <- complex(real = c(rnorm(1), RW, rnorm(1), RW[(N/2-1):1]), 
                  imaginary = c(0, IW, 0, -IW[(N/2-1):1]), length.out=N)
     # Those complex numbers that are to be back transformed for Fourier Frequencies 0, 2pi/N, 2*2pi/N, ..., pi, ..., 2pi-1/N 
     # Choose in a way that frequencies are complex-conjugated and symmetric around pi 
     # 0 and pi do not need an imaginary part
    reihe <- fft(fR, inverse=TRUE) # go back into time domain
    return(Re(reihe)) # imaginary part is 0
}

and this works perfectly :

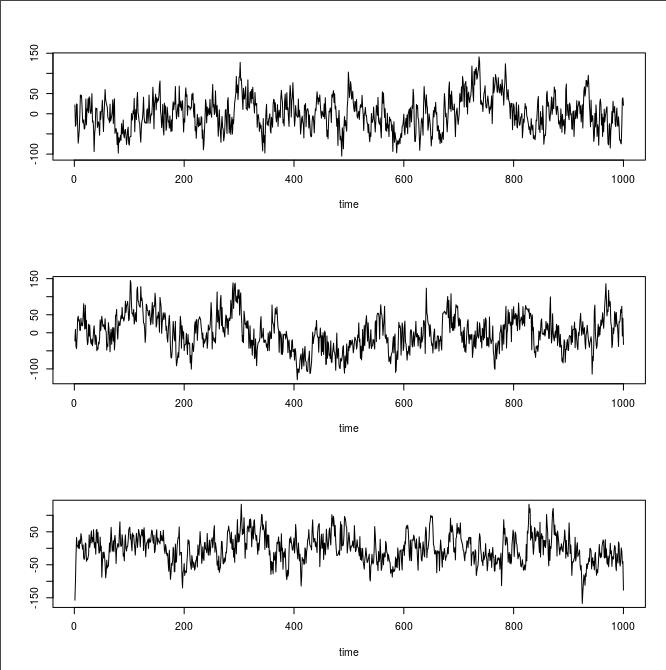
par(mfrow=c(3,1))
replicate(3,plot(TK95(1000,1),type="l",ylab="",xlab="time"))

Tenure