So, this is really a comment to desertnaut's answer but I can't comment on it yet due to my reputation. As he pointed out, your version is only correct if your input consists of a single sample. If your input consists of several samples, it is wrong. However, desertnaut's solution is also wrong. The problem is that once he takes a 1-dimensional input and then he takes a 2-dimensional input. Let me show this to you.
import numpy as np
# your solution:
def your_softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
# desertnaut solution (copied from his answer):
def desertnaut_softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0) # only difference
# my (correct) solution:
def softmax(z):
assert len(z.shape) == 2
s = np.max(z, axis=1)
s = s[:, np.newaxis] # necessary step to do broadcasting
e_x = np.exp(z - s)
div = np.sum(e_x, axis=1)
div = div[:, np.newaxis] # dito
return e_x / div
Lets take desertnauts example:
x1 = np.array([[1, 2, 3, 6]]) # notice that we put the data into 2 dimensions(!)
This is the output:
your_softmax(x1)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
desertnaut_softmax(x1)
array([[ 1., 1., 1., 1.]])
softmax(x1)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
You can see that desernauts version would fail in this situation. (It would not if the input was just one dimensional like np.array([1, 2, 3, 6]).
Lets now use 3 samples since thats the reason why we use a 2 dimensional input. The following x2 is not the same as the one from desernauts example.
x2 = np.array([[1, 2, 3, 6], # sample 1
[2, 4, 5, 6], # sample 2
[1, 2, 3, 6]]) # sample 1 again(!)
This input consists of a batch with 3 samples. But sample one and three are essentially the same. We now expect 3 rows of softmax activations where the first should be the same as the third and also the same as our activation of x1!
your_softmax(x2)
array([[ 0.00183535, 0.00498899, 0.01356148, 0.27238963],
[ 0.00498899, 0.03686393, 0.10020655, 0.27238963],
[ 0.00183535, 0.00498899, 0.01356148, 0.27238963]])
desertnaut_softmax(x2)
array([[ 0.21194156, 0.10650698, 0.10650698, 0.33333333],
[ 0.57611688, 0.78698604, 0.78698604, 0.33333333],
[ 0.21194156, 0.10650698, 0.10650698, 0.33333333]])
softmax(x2)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047],
[ 0.01203764, 0.08894682, 0.24178252, 0.65723302],
[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
I hope you can see that this is only the case with my solution.
softmax(x1) == softmax(x2)[0]
array([[ True, True, True, True]], dtype=bool)
softmax(x1) == softmax(x2)[2]
array([[ True, True, True, True]], dtype=bool)
Additionally, here is the results of TensorFlows softmax implementation:
import tensorflow as tf
import numpy as np
batch = np.asarray([[1,2,3,6],[2,4,5,6],[1,2,3,6]])
x = tf.placeholder(tf.float32, shape=[None, 4])
y = tf.nn.softmax(x)
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(y, feed_dict={x: batch})
And the result:
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037045],
[ 0.01203764, 0.08894681, 0.24178252, 0.657233 ],
[ 0.00626879, 0.01704033, 0.04632042, 0.93037045]], dtype=float32)


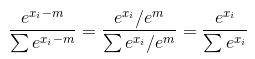
-inf to +infto-inf to 0. I guess I was overthinking. hahahaaa – Catechismaxis = 0in the suggested answer by Udacity? – Midsummerexp– Eighth