How to rewrite an expression in terms of an other expression in sympy

Question

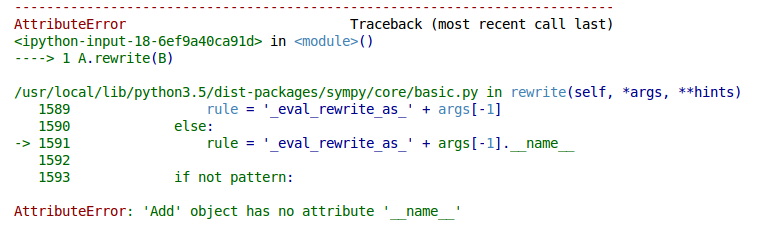
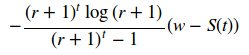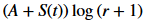EDIT: I am not asking how to solve an equation in terms of a given variable (as in this supposed duplicated question), but how to represent an expression in terms of an other one, as specified in the question. I believe it is the "duplicated" question to have a misleading title.

I am very new with SymPy. I have an expression that, once expressed in terms to an other expression, should become very nice. The problem is that I don't know how to "force" to express the original expression in terms of the other one.

This is a basic example:

import sympy as sp
sp.init_printing(use_unicode=True)
a,b,c =  sp.symbols('a b c')
A = a+b+c
B = a+c
C = A.subs(a+c,B) #  Expected/wanted: C = B+b
C

A.rewrite(B)

A and B could be rather complex expressions. For reference, this is my real-case scenario:

import sympy as sp
sp.init_printing(use_unicode=True)
t, w, r = sp.symbols('t w r')
S = sp.Function('S')(t)
V = (S-w*(1+r)**t)/(((1+r)**t)-1)
V

St = -(r + 1)**t*(w - S)*sp.log(r + 1)/((r + 1)**t - 1)
St 

Once I write St in terms of V, I should be able to simplify to get just

St = rS(t)+rV

But I am unable to do it in SymPy.

Hae

Answer 1

First note that when you do something like

a,b,c =  sp.symbols('a b c')
A = a+b+c
B = a+c

variables A, B are not new Sympy symbols that Sympy can understand and operate on, rather, they are aliases for the Sympy expressions a+b+c and a+c, respectively. Therefore, A.subs(a+c,B) is essentially the same as A.subs(a+c,a+c), which is, of course, meaningless. You get the idea of why A.rewrite(B) is also of no use.

I do not think that calls like expr.subs({complicated_mutlivariable_formula: new_variable}) work in Sympy. One way to do what you want is to first solve the equation complicated_mutlivariable_formula = new_variable with respect to one of the "old" variables, and, assuming a unique solution exist, use subs() to substitute this variable.

Applying this approach for the second example:

# sympy Symbol A will be used to represent expression V
A = sp.symbols('A') 

# Solve the equation V==A with respect to w, which has a unique solution as a function of A
w_A = sp.solve(sp.Eq(V,A), w)[0] 

# Now substitute w 
St.subs({w:w_A}).simplify()

Johm