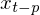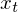statespace.SARIMAX model: why the model use all the data to train mode, and predict the a range of train model

Question

I followed the tutorial to study the SARIMAX model: https://www.digitalocean.com/community/tutorials/a-guide-to-time-series-forecasting-with-arima-in-python-3. The date range of data is 1958-2001.

mod = sm.tsa.statespace.SARIMAX(y,
                                order=(1, 1, 1),
                                seasonal_order=(1, 1, 1, 12),
                                enforce_stationarity=False,
                                enforce_invertibility=False)

results = mod.fit()

when are fitting an ARIMA Time Series Model, I found the author all date range data to fit parameter of model. But when validating Forecasts, the author used date started from 1998-01-01 as one part of date range of data for fitting model.

pred = results.get_prediction(start=pd.to_datetime('1998-01-01'), dynamic=False)

I know in machine learning model, the training data and validation(test) data is different, I mean different range. I mean the author is right? why do like this(I mean the reason touse all train data), I a new one to SARIMAX model.

Could you guys tell me more about this model, for example how about predict days or weeks not just month, I mean how to set the parameter of order=(1,1,1), seasonal_order=(1, 1, 1, 12). Thanks!

Devlin

Answer 1

The author is right. When you do a regression (linear, higher-order or logistic - doesn't matter) - it is absolutely ok to have deviations from your training data (for instance - logistic regression even on training data may give you a false positive).

Same stands for time series. I think this way the author wanted to show that the model is built correctly.

seasonal_order=(1, 1, 1, 12)

If you look at tsa stats documentation you will see that if you want to operate with quarterly data - you have to assign the last parameter (s) - value of 4. Monthly - 12. It means that if you want to operate with weekly data seasonal_order should look like this

seasonal_order=(1, 1, 1, 52)

daily data will be

seasonal_order=(1, 1, 1, 365)

order component is the parameter that is responsible for non-seasonal parameters p, d and q respectively. You have to find them depending on your data behaviour

• p. You can interpret it as wether has an influence on . Or in other words, if you have a daily data and p is 6 you can understand it as wether Tuesday data will have an influence on Sunday data.
• d. Differencing parameter. It defines the level of integration of your process. It means how many times you should apply time series differencing operator in order to make your time series stationary
• q. You can interpret it as how many prior noises (errors) affect the current value

Here is a good answer how you can find non-seasonal component values

Gleiwitz

thanks @papadoble151, If possible, could you tell me how to set the order parameter:order(1,1,1) for week and day predict. I know week is almost the same with month(1,1,1). what about the day predict? – Devlin

@Devlin these parameters (p,d,q) - you have to find them. There is no predefined set of values for daily or weekly data. Always try to find some intuitive explanation to every parameter. This is a great place to learn about time series otexts.org/book/fpp – Gleiwitz

thanks @Gleiwitz for your kind answer. I will accept your answer. By the way, could you provide me with you contact way or blog site so that we can communicate with each other about time series model. – Devlin

@tktktk0711, just add gmail.com to my nickname – Gleiwitz

Hi @Gleiwitz when I set the seasonal_order=(1, 1, 1, 365) for days prediction, I found that I take a lot of time and no result. I don't know why. – Devlin

If I have data every 15 minute? will be 365 *(4*24)? where 4 is values in one hour and 24 is hours for days @Gleiwitz It's ok if my dataset isn't full of data? (not all values for one year) – Prajna

@Prajna yes, it should be (365 * 4 * 24) provided there are no gaps in your data. In general, it is not ok if your data has gaps, because you will have a shift in seasonal component – Gleiwitz

So if I have a snapshot of one year (like 14days) with gaps isn't work? – Prajna

@Prajna it is really hard to say. It may work, but you may experience weaker model performance after the gaps have occured in the training data – Gleiwitz

Worth noting that the seasonal periodicity is exactly that: the period of the cyclical pattern you re interested in. If you have daily data and the cyclical pattern you want to study is annual, you should use 365 for the periodicity. However, if your main cycle is weekly, you will want to use 7. Or if it's monthly, 30. Similarly, if you have quarterly data but are are studying something with multi-year cycles, 4 is not necessarily right, maybe it's 11 years = 44 quarters (e.g. for solar activity). – Quinidine

Answer 2

The author of the blog set those parameters because: "The output of our code suggests that SARIMAX(1, 1, 1)x(1, 1, 1, 12) yields the lowest AIC."

Siamang