How to truly calculate a spherical voronoi diagram using sf?

Question

I want to make a world map with a voronoi tessellation using the spherical nature of the world (not a projection of it), similar to this using D3.js, but with R.

As I understand ("Goodbye flat Earth, welcome S2 spherical geometry") the sf package is now fully based on the s2 package and should perform as I needed. But I don't think that I am getting the results as expected. A reproducible example:

library(tidyverse)
library(sf)
library(rnaturalearth)
library(tidygeocoder)

# just to be sure
sf::sf_use_s2(TRUE)

# download map 
world_map <- rnaturalearth::ne_countries(
                scale = 'small', 
                type = 'map_units',
                returnclass = 'sf')

# addresses that you want to find lat long and to become centroids of the voronoi tessellation 
addresses <- tribble(
~addr,
"Juneau, Alaska" ,
"Saint Petersburg, Russia" ,
"Melbourne, Australia" 
)

# retrive lat long using tidygeocoder
points <- addresses %>% 
          tidygeocoder::geocode(addr, method = 'osm')

# Transform lat long in a single geometry point and join with sf-base of the world
points <- points %>% 
          dplyr::rowwise() %>% 
          dplyr::mutate(point = list(sf::st_point(c(long, lat)))) %>% 
          sf::st_as_sf() %>% 
          sf::st_set_crs(4326)

# voronoi tessellation
voronoi <- sf::st_voronoi(sf::st_union( points ) ) %>% 
     sf::st_as_sf() %>% 
     sf::st_set_crs(4326)

# plot
ggplot2::ggplot() +
    geom_sf(data = world_map,
            mapping = aes(geometry = geometry), 
            fill = "gray95") +
    geom_sf(data = points,
            mapping = aes(geometry = point),
            colour = "red") +
    geom_sf(data = voronoi,
            mapping = aes(geometry = x),
            colour = "red",
            alpha = 0.5)  

The whole Antarctica should be closer to Melbourne than to the other two points. What am I missing here? How to calculate a voronoi on a sphere using sf?

Stockjobber

I don't see anything new: the documentation still has the same warnings: r-spatial.github.io/sf/articles/sf7.html . Maybe ask on the S2 mailing list ? – Intercalation

Hi Ben, glad you are back! Maybe I should refraime my question to "how to truly calculate... using R" (different from "using sf"), or maybe open a new question altogether. – Stockjobber

From here (#546370) I tried, with no success (my own coding inability) calling a fortran subroutines (people.sc.fsu.edu/~jburkardt/f_src/sphere_voronoi/…) and brifly fiddle with calling CDAL (doc.cgal.org/latest/Triangulation_3/index.html) via RcppCGAL. Maybe I should give the route that uses reticulate + SciPy (docs.scipy.org/doc/scipy/reference/generated/…) a new try. – Stockjobber

In any case I only see ways foward using other languages (Fortran, C, python, javascript/D3), and I am not versed in any of those... – Stockjobber

With sf I don't know, but you could try the sphericalTessellation package instead. – Watersick

Answer 1

Here's a method that builds on Stéphane Laurent's approach, but outputs sf objects.

Let us obtain an sf object of all the world capitals:

library(sf)
#> Linking to GEOS 3.9.3, GDAL 3.5.2, PROJ 8.2.1; sf_use_s2() is TRUE

capitals <- do.call(rbind,
  subset(maps::world.cities, capital == 1, select = c("long", "lat")) |>
  as.matrix() |>
  asplit(1) |>
  lapply(st_point) |>
  lapply(st_sfc) |>
  lapply(st_sf, crs = 'WGS84')) |>
  `st_geometry<-`('geometry') |>
  cbind(city = subset(maps::world.cities, capital == 1, select = c("name")))

capitals
#> Simple feature collection with 230 features and 1 field
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -176.13 ymin: -51.7 xmax: 179.2 ymax: 78.21
#> Geodetic CRS:  WGS 84
#> First 10 features:
#>           name               geometry
#> 1       'Amman    POINT (35.93 31.95)
#> 2    Abu Dhabi    POINT (54.37 24.48)
#> 3        Abuja      POINT (7.17 9.18)
#> 4        Accra      POINT (-0.2 5.56)
#> 5    Adamstown  POINT (-130.1 -25.05)
#> 6  Addis Abeba     POINT (38.74 9.03)
#> 7        Agana   POINT (144.75 13.47)
#> 8      Algiers     POINT (3.04 36.77)
#> 9        Alofi POINT (-169.92 -19.05)
#> 10   Amsterdam     POINT (4.89 52.37)

And our world map:

world_map <- rnaturalearth::ne_countries(
  scale = 'small', 
  type = 'map_units',
  returnclass = 'sf')

Now we use Stéphane Laurent's approach to tesselate the sphere, but then reverse the projection back into spherical co-ordinates. This allows translation back to sf, though we have to be careful to split any objects that "wrap around" the 180/-180 longitude line:

voronoi <- capitals %>%
  st_coordinates() %>%
  `*`(pi/180) %>%
  cbind(1) %>%
  pracma::sph2cart() %>%
  sphereTessellation::VoronoiOnSphere() %>%
  lapply(\(x) rbind(t(x$cell), t(x$cell)[1,])) %>%
  lapply(\(x) {
    n <- nrow(x) - 1
    lapply(seq(n), function(i) {
      a <- approx(x[i + 0:1, 1], x[i + 0:1, 2], n = 1000)
      b <- approx(x[i + 0:1, 1], x[i + 0:1, 3], n = 1000)
      d <- cbind(a$x, a$y, b$y) |> pracma::cart2sph() 
      d <- d[,1:2] * 180/pi
      if(max(abs(diff(d[,1]))) > 180) {
        s <- which.max(abs(diff(d[,1])))
        d <- list(d[1:s, ], d[(s+1):nrow(d),])
      }
      d })}) |>
  lapply(\(x) {
    st_geometrycollection(lapply(x, \(y) {
    if(class(y)[1] == "list") {
      st_multilinestring(y)
      } else {
        st_linestring(y)
      }}))}) %>%
  lapply(st_sfc) %>%
  lapply(st_sf, crs = 'WGS84') %>%
  {do.call(rbind, .)} %>%
  `st_geometry<-`('geometry')

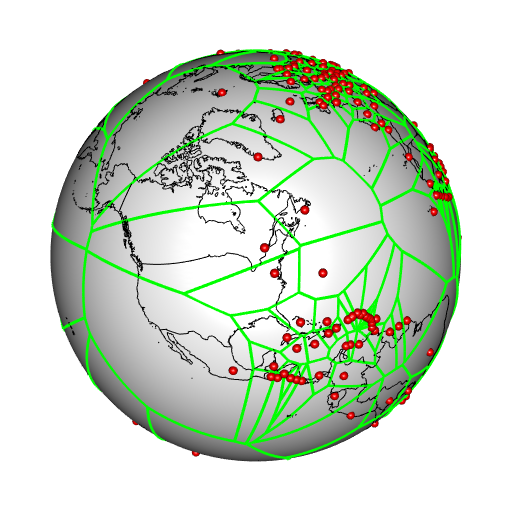
Now we have our Voronoi grid as an sf object, so we can plot it using ggplot:

library(ggplot2)

ggplot() +
  geom_sf(data = world_map, fill = "cornsilk", color = NA) +
  geom_sf(data = voronoi, color = "gray40") +
  geom_sf(data = capitals, color = "black", size = 0.2) + 
  coord_sf(crs = "ESRI:53011") +
  theme(panel.background = element_rect(fill = "lightblue"))

---

Addendum

Although the above solution works for drawing tesselations over the whole globe, if we want to get polygons of land areas only, we can do it as follows:

First, we make a union of all land masses from our world map

wm <- st_make_valid(world_map) |> st_union()

Now we get the co-ordinates of the vertices of our Voronoi tiles:

pieces <- capitals %>%
  st_coordinates() %>%
  `*`(pi/180) %>%
  cbind(1) %>%
  pracma::sph2cart() %>%
  sphereTessellation::VoronoiOnSphere() %>%
  lapply(\(x) rbind(t(x$cell), t(x$cell)[1,])) %>%
  lapply(pracma::cart2sph) %>%
  lapply(\(x) x[,1:2] * 180/pi)

Now we need to find tiles that span the -180 / 180 line:

complete <- pieces %>% sapply(\(x) abs(diff(c(min(x[,1]), max(x[,1])))) < 180)

We now split these and turn them into multipolygons, finding their intersection with the world map:

orphans <- pieces[!complete] %>%
  lapply(\(x) {x[,1] + 180 -> x[,1]; x}) %>%
  lapply(\(x) st_polygon(list(x)) |> st_sfc(crs = "WGS84")) %>%
  lapply(\(x) {
    west <- st_intersection(x, matrix(c(-180, -0.001, -0.001, -180, -180, 
                                 -89, -89, 89, 89, -89), ncol = 2) |>
                                list() |> st_polygon() |> st_sfc(crs = "WGS84"))
    east <- st_intersection(x, matrix(c(0, 180, 180, 0, 0, 
                                        -89, -89, 89, 89, -89), ncol = 2) |>
                              list() |> st_polygon() |> st_sfc(crs = "WGS84"))
    west <- st_coordinates(west)[,1:2]
    east <- st_coordinates(east)[,1:2]
    west[,1] <- west[,1] + 180
    east[,1] <- east[,1] - 180
    w <- st_polygon(list(west)) |> st_sfc(crs = "WGS84") |> st_intersection(wm)
    e <- st_polygon(list(east)) |> st_sfc(crs = "WGS84") |> st_intersection(wm)
    st_combine(st_union(e, w))
  }) %>%
  lapply(st_sf) %>%
  lapply(\(x) { if(nrow(x) > 0) { st_segmentize(x, 100000) } else {
    st_point(matrix(c(0, 0), ncol = 2)) |> 
      st_sfc(crs = "WGS84") |> st_sf()
  }
  }) %>% 
  lapply(\(x) `st_geometry<-`(x, 'geometry')) %>%
  {do.call(rbind, .)} %>%
  cbind(city = capitals$name[!complete])

We can do intersections for the non-wraparound tiles like this:

non_orphans <- pieces %>%
  subset(complete) %>%
  lapply(list) %>%
  lapply(st_polygon) %>%
  lapply(st_sfc, crs = "WGS84") %>%
  lapply(st_intersection, y = wm) %>%
  lapply(st_sf) %>%
  lapply(\(x) { if(nrow(x) > 0) { st_segmentize(x, 100000) } else {
    st_point(matrix(c(0, 0), ncol = 2)) |> 
      st_sfc(crs = "WGS84") |> st_sf()
  }
  }) %>%
  lapply(\(x) `st_geometry<-`(x, 'geometry')) %>%
  {do.call(rbind, .)} %>%
  cbind(city = capitals$name[complete])

Finally, we bind all these together into a single sf object:

voronoi <- rbind(orphans, non_orphans)
voronoi <- voronoi[!st_is_empty(voronoi),]
voronoi <- voronoi[sapply(voronoi$geometry, \(x) class(x)[2] != "POINT"),]

Now we're ready to plot. Let's define a palette function that gives results similar to your linked example:

f <- colorRampPalette(c("#dae7b4", "#c5b597", "#f3dca8", "#b4b6e7", "#d6a3a4"))

We'll also create a background "globe" and a smoothed grid to draw over our map, as in the example:

grid <- lapply(seq(-170, 170, 10), \(x) rbind(c(x, -89), c(x, 0), c(x, 89))) |>
  lapply(st_linestring) |>
  lapply(\(x) st_sfc(x, crs = "WGS84")) |>
  lapply(\(x) st_segmentize(x, dfMaxLength = 100000)) |>
  c(
    lapply(seq(-80, 80, 10), \(x) rbind(c(-179, x), c(0, x), c(179, x))) |>
      lapply(st_linestring) |>
      lapply(\(x) st_sfc(x, crs = "WGS84"))
  ) |>
  lapply(st_sf) |>
  lapply(\(x) `st_geometry<-`(x, 'geometry')) %>%
  {do.call(rbind, .)}

globe <- st_polygon(list(cbind(c(-179, 179, 179, -179, -179), 
                               c(-89, -89, 89, 89, -89)))) |> 
  st_sfc(crs = "WGS84") |> 
  st_segmentize(100000)

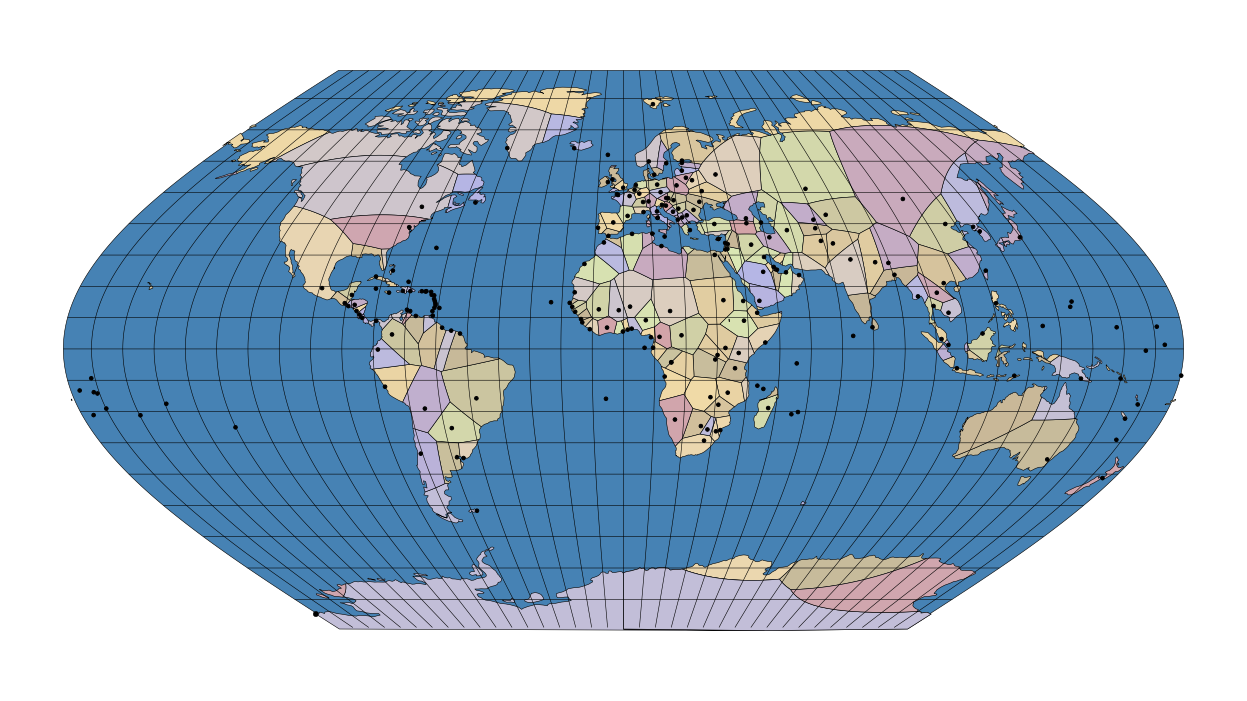
The final result is a faithful sf version of the linked example:

ggplot() +
  geom_sf(data = globe, fill = "#4682b4", color = "black") +
  geom_sf(data = voronoi, color = "black", aes(fill = city)) +
  geom_sf(data = capitals, color = "black", size = 1) + 
  geom_sf(data = grid, color = "black", linewidth = 0.2) +
  coord_sf(crs = "ESRI:53011") +
  scale_fill_manual(values = f(nrow(voronoi))) +
  theme(panel.background = element_blank(),
        legend.position = "none",
        panel.grid = element_blank())

^{Created on 2023-06-24 with reprex v2.0.2}

Baryon

That is amazing! The power of the stackoverflow R heroes Stéphane Laurent and Allan Cameron chipping in code! Thanks! I wish I could split the bounty between the two of you. – Stockjobber

What a juicy addendum!! Thanks Allan! – Stockjobber

Answer 2

With sf I don't know, but you can use the sphereTessellation package instead.

library(pracma) # for the sph2cart function
library(maps)
data(world.cities)
data(worldMapEnv)

world <- map("world", plot = FALSE)
countries <- sph2cart(cbind(world$x*pi/180, world$y*pi/180, 1))

capitals_ll <- as.matrix(
    subset(world.cities, capital == 1, select = c("long", "lat"))
) * pi / 180
capitals <- sph2cart(cbind(capitals_ll, 1))


library(rgl)
open3d(windowRect = 50 + c(0, 0, 512, 512), zoom = 0.7)
sphereMesh <- Rvcg::vcgSphere()
shade3d(sphereMesh, color = "cyan", polygon_offset = 1)
lines3d(countries)
points3d(capitals, size = 4, color = "red")
snapshot3d("world.png", webshot = FALSE)

library(sphereTessellation)
vor <- VoronoiOnSphere(capitals)
open3d(windowRect = 50 + c(0, 0, 512, 512), zoom = 0.7)
plotVoronoiOnSphere(
    vor, colors = "white", edges = TRUE, ecolor = "green",
    sites = TRUE, scolor = "red", polygon_offset = 1
)
lines3d(countries)
snapshot3d("world_voronoi.png", webshot = FALSE)

But I don't know how we could clip the Voronoï cells to the countries.

Rohn

Thank you very much Stéphane! Amazing job with your package! – Stockjobber

I managed to create an sf solution that borrows heavily from your approach Stephane. I resolved the issue you had by using st_intersection – Baryon

@AllanCameron Awesome. Is the tessellation periodic? (mappable on a sphere). I don't know sf (yet). – Watersick

@StéphaneLaurent the tessellation is just the output from VoronoiOnSphere, so it is the same as the one you produced except to the best of my knowledge, it can not be periodic in sf. Although the tesselation can be mapped onto a sphere, there will always be a discontinuity at the boundaries of the coordinate system used. In the projection I use in my answer, the discontinuity is at the international date line (180 degrees longitude). In this case, that doesn't matter too much because there are few land masses that bridge this line (Eastern tip of Russia and Antarctica) – Baryon

@StéphaneLaurent in fact, the discontinuity is a bit of a pain, as you need to ensure anything that crosses the date line is split into pieces (manually). That's the main reason my code is so long. – Baryon

@AllanCameron Aah I didn't see you use my package. – Watersick

Yes, I didn't know of any other way to get the tessellation on a sphere (without reinventing the wheel). Nice job on the package. sf has some great functionality for spherical co-ordinates, including Boolean operators on polygons. It's also very useful for (2D) Cartesian co-ordinates and is smple to use (though hard to master - I'm no expert myself) – Baryon

@AllanCameron actually you can split (and subsequently rejoin) polygons that cross the date line quite easily. Have a look at https://mcmap.net/q/1014723/-visual-bug-when-changing-robinson-projection-39-s-central-meridian-with-ggplot2 and https://mcmap.net/q/1014723/-visual-bug-when-changing-robinson-projection-39-s-central-meridian-with-ggplot2 – Brimful

@Brimful I have more-or-less done this in my answer, but if there is a way to do it more elegantly and have all the pieces joined up at the end, it would be great to see. If you get a chance, please post an answer, even if it builds on existing answers. This feels like it requires a community effort to get an optimal result. – Baryon

Answer 3

(This answer doesn't tell you how to do it, but does tell you what's going wrong.)

When I ran this code I got

Warning message: In st_voronoi.sfc(sf::st_union(points)) : st_voronoi does not correctly triangulate longitude/latitude data

From digging into the code it looks like this is a known limitation. Looking at the C++ code for CPL_geos_voronoi, it looks like it directly calls a GEOS method for building Voronoi diagrams. It might be worth opening an sf issue to indicate that this is a feature you would value (if no-one tells the developer that particular features would be useful, they don't get prioritized ...) It doesn't surprise me that GEOS doesn't automatically do computations that account for spherical geometry. Although the S2 code base mentions Voronoi diagrams in a variety of places, it doesn't look like there is a drop-in replacement for the GEOS algorithm ... there are a variety of implementations in other languages for spherical Voronoi diagrams (e.g. Python), but someone would probably have to port them to R (or C++) ...

If I really needed to do this I would probably try to figure out how to call the Python code from within R (exporting the data from sf format to whatever Python needs, then re-importing the results into an appropriate sf format ...)

Printing the code for sf:::st_voronoi.sfc:

function (x, envelope = st_polygon(), dTolerance = 0, bOnlyEdges = FALSE) 
{
    if (compareVersion(CPL_geos_version(), "3.5.0") > -1) {
        if (isTRUE(st_is_longlat(x))) 
            warning("st_voronoi does not correctly triangulate longitude/latitude data")
        st_sfc(CPL_geos_voronoi(x, st_sfc(envelope), dTolerance = dTolerance, 
            bOnlyEdges = as.integer(bOnlyEdges)))
    }
    else stop("for voronoi, GEOS version 3.5.0 or higher is required")
}

In other words, if the GEOS version is less than 3.5.0, the operation fails completely. If it is >= 3.5.0 (sf:::CPL_geos_version() reports that I have version 3.8.1), and long-lat data is being used, a warning is supposed to be issued (but the computation is done anyway).

The first time I ran this I didn't get the warning; I checked and options("warn") was set to -1 (suppressing warnings). I'm not sure why — running from a clean session did give me the warning. Maybe something in the pipeline (e.g. rnaturalearth telling me I needed to install the rnaturalearthdata package) accidentally set the option?

Intercalation

Thank you for your research on the topic. For now I agree on the paths that you highlighted: a) open a issue on git and b) reticulate + SciPy (although I don't have the knowledge yet to do so). Thanks!! – Stockjobber

If this "solved" (sort of) your problem you are encouraged to click on the check-mark to accept it (although you could always leave it open in the hope that someone else will show up and provide a complete solution rather than just a diagnosis ...) – Intercalation

Yeah, I don´t really know the stackoverflow etiquette in this case (I am new on the site). I guess I will put an issue on git and a link to here, and leave it open for a few more days. – Stockjobber

For future reference: untill now, s2 does not provide Voronoi computations. – Stockjobber

You can leave it open indefinitely. You would also be welcome to (1) rescind the check-mark (a question might be slightly more likely to get attention if it doesn't have an accepted answer), (2) if someone comes along and provides a better answer (including you!), move the check-mark to a different answer. – Intercalation