How to fix ROC curve with points below diagonal?

Question

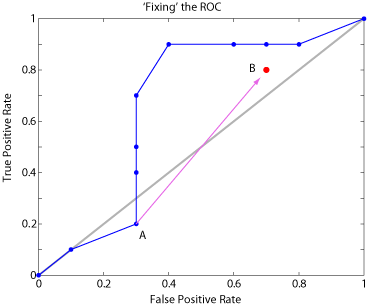
I am building receiver operating characteristic (ROC) curves to evaluate classifiers using the area under the curve (AUC) (more details on that at end of post). Unfortunately, points on the curve often go below the diagonal. For example, I end up with graphs that look like the one here (ROC curve in blue, identity line in grey) :

The the third point (0.3, 0.2) goes below the diagonal. To calculate AUC I want to fix such recalcitrant points.

The standard way to do this, for point (fp, tp) on the curve, is to replace it with a point (1-fp, 1-tp), which is equivalent to swapping the predictions of the classifier. For instance, in our example, our troublesome point A (0.3, 0.2) becomes point B (0.7, 0.8), which I have indicated in red in the image linked to above.

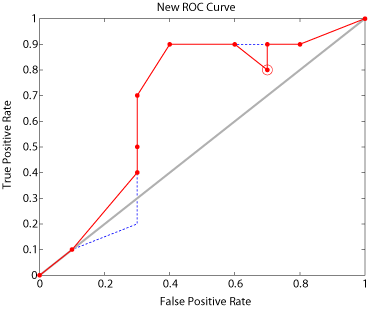
This is about as far as my references go in treating this issue. The problem is that if you add the new point into a new ROC (and remove the bad point), you end up with a nonmonotonic ROC curve as shown (red is the new ROC curve, and dotted blue line is the old one):

And here I am stuck. How can I fix this ROC curve?

Do I need to re-run my classifier with the data or classes somehow transformed to take into account this weird behavior? I have looked over a relevant paper, but if I am not mistaken, it seems to be addressing a slightly different problem than this.

In terms of some details: I still have all the original threshold values, fp values, and tp values (and the output of the original classifier for each data point, an output which is just a scalar from 0 to 1 that is a probability estimate of class membership). I am doing this in Matlab starting with the perfcurve function.

---

Linettelineup

Are you using cross-validation and do you have any idea of the confidence intervals on your curves? Depending on where you are in building your classifier, this may not be something to worry about. The shape depends on the test cases and is smoothed as you combine estimates from cross-validation. – Ensign

I plan to build a set of ROC curves, but am just focusing on individuals right now, constructed from individual runs of an artificial neural net (well, technically, I construct the ROC from the k neural networks I trained using k-fold cross validated classification using the ANN). I suppose I can just run it 100 times, and look at the distribution of ROC curves (or, area under ROC, and if the area is less than .5, I can just swap it for 1-AUC). Do you think that is reasonable? It sure would be simpler! – Linettelineup

What about an algorithm that does three things: first, if AUC<.5, then reverse the classifier (so AUC=1-AUC). Second, once this coarse correction is made, for those points in which tp<fp, set tp=fp. Then, recalculate AUC for this corrected classifier. – Linettelineup

I wouldn't worry about ugliness until you have a better estimate of the ROC curve. One way to do this is to add an outer cross-validation process, splitting the data into testing and training, with the training data going into your current process. Get the average and uncertainty of your ROC curve from the outer process. This average ROC curve should be a smoother, more reliable estimate of performance. – Ensign

That is a good idea, though I am already doing k-fold cross validation to train my neural network, so my sample size is already stretched to its limit. You are basically talking about running an optimization algorithm in which AUC (or something like that) is the objective function, no? The data demands are growing for my little data sets (typically I have from 100-200 trials). Or am I missing something? – Linettelineup

Hmmm, I don't think it is an optimization algorithm, it is just an unbiased test of performance. The main drawback to nested cross-validation is usually thought to be computation time, rather than data use. I think there are two issues here. One is that your estimates of performance will be too optimistic. The classic paper is Varma and Simon ncbi.nlm.nih.gov/pmc/articles/PMC1397873 but there is a large literature. The second issue is that the ROC curve (and even more the AUC) is sensitive to the test data, for example balance of class membership. – Ensign

let us continue this discussion in chat – Ensign

Answer 1

Note based on some very helpful emails about this from the people that wrote the articles cited above, and the discussion above, the right answer seems to be: do not try to "fix" individual points in an ROC curve unless you build an entirely new classifier, and then be sure to leave out some test data to see if that was a reasonable thing to do.

Getting points below the identity line is something that simply happens. It's like getting an individual classifier that scores 45% correct even though the optimal theoretical minimum is 50%. That's just part of the variability with real data sets, and unless it is significantly less than expected based on chance, it isn't something you should worry too much about. E.g., if your classifier gets 20% correct, then clearly something is amiss and you might look into the specific reasons and fix your classifier.

Linettelineup

Answer 2

Yes, swapping a point for (1-fp, 1-tp) is theoretically effective, but increasing sample size is a safe bet too.

It does seem that your system has a non-monotonic response characteristic so be careful not to bend the rules of the ROC too much or you will impact the robustness of the AUC.

That said, you could try to use a Pareto Frontier Curve (Pareto Front). If that fits the requirements of "Repairing Concavities" then you'll basically sort the points so that the ROC curve becomes monotonic.

Plautus

I've seen this with huge data sets, so I think this isn't an issue of sample size. My example is just a cartoon to show the problem. The core issue, I think, is having a classifier that is not making optimal use of the information in the data. The "trick" I mentioned works because it effectively builds a new classifier by swapping the original classifier's predictions at a given threshold value. The problem is that doing this simple fix at one threshold doesn't update all the other fp and tp estimates already calculated in the original run of the algorithm. And I am not sure how to do this. – Linettelineup

Thanks for the clarification on the figures. I have updated my answer to include an approach with a Pareto Front. – Plautus

That seems like an interesting approach, and is one I was considering. The reason I am cautious is that it seems to effectively create a suboptimal classifier for the points to the left of the new transformed point B. However, this may be the best we can do. I am also thinking there must be some standard solution here that people in the know use. In terms of "bending the rules" of ROC, I think that isn't too much of a worry because points below the diagonal show your classifier is acting weird and needs to be tweaked: in theory no points should be below the diagonal. – Linettelineup

Thanks. Yes, perhaps it isn't worth it, this typically only happens for cases where the feature doesn't classify very well. However, if you end up with an ROC that is completely below the line, then the fix is easy: simply reverse all the predictions of your original classifier. However, a few points, here and there, below the line, may be something I shouldn't worry too much about. – Linettelineup