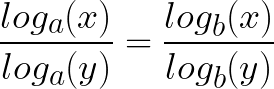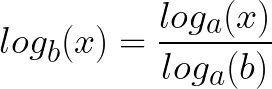When to use which base of log for tf-idf?

Question

I'm working on a simple search engine where I use the TF-IDF formula to score how important a search word is. I see people using different bases for the formula, but I see no explanation for when to use which. Does it matter at all, and do you have any recommendations?

My current implementation uses the regular log() function of the math.h library

Zarla

Answer 1

TF-IDF literature usually uses base 2, although a common implementation sklearn uses natural logarithms for example. Just take in count that the lower the base, the bigger the score, which can affect truncation of search resultset by score.

Note that from a mathematical point of view, the base can always be changed later. It's easy to convert from one base to another, because the following equality holds:

log_a(x)/log_a(y) = log_b(x)/log_b(y)

You can always convert from one base to another. It's actually very easy. Just use this formula:

log_b(x) = log_a(x)/log_a(b)

Often bases like 2 and 10 are preferred among engineers. 2 is good for halftimes, and 10 is our number system. Math people prefer the natural logarithm, because it makes calculus a lot easier. The derivative of the function b^x where b is a constant is k*b^x. Bur if b is equal to e (the natural logarithm) then k is 1.

So let's say that you want to send in the 2-logarithm of 5.63 using log(). Just use log(5.63)/log(2).

If you have the need for it, just use this function for arbitrary base:

// Returns the b-logarithm of x
double logb(double x, double b) {
    return log(x)/log(b);
}

Ido