Algorithm for placing a grid over a disordered set of points

Question

Given a large set (tens of thousands up to millions) of disordered points represented as 3D Cartesian vectors, what's a good algorithm for making a regular square grid (of user-defined spacing) that encloses all of the points? Some constraints:

1. The grid needs to be square and regular
2. I need to be able to adjust the grid spacing (the length of a side of one of the squares), ideally with a single variable
3. I want a grid of minimum size, ie every 'block' in the grid should contain at least one of the disordered points, and every disordered point should be enclosed in a 'block'
4. The return value of the algorithm should be the list of coordinates of the grid points

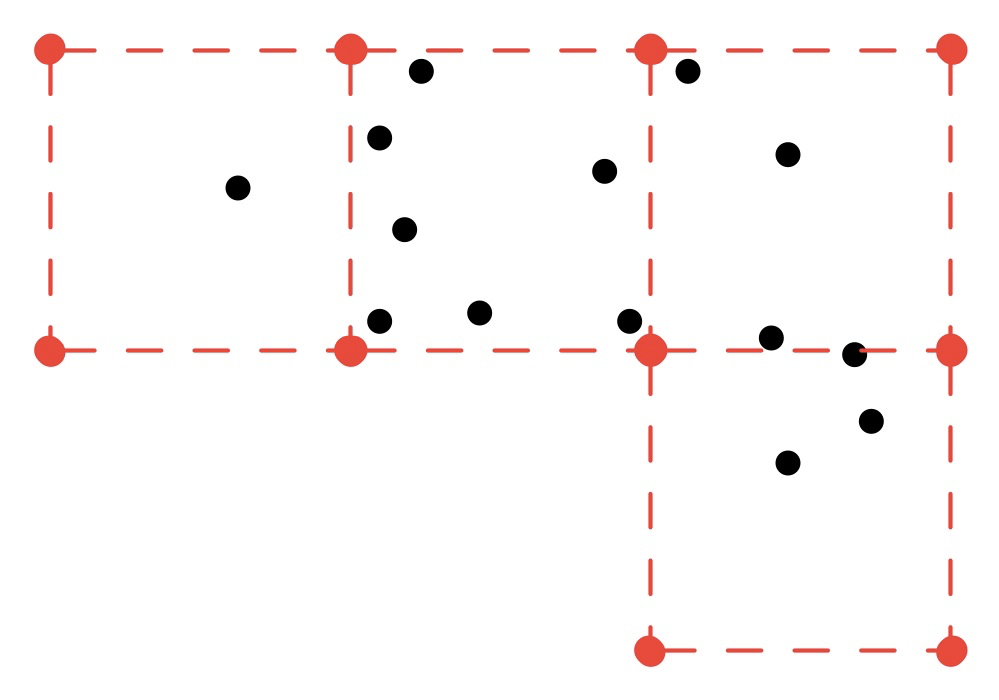
To illustrate in 2D, given this set of points:

for some grid spacing X, one possible return value of the algorithm would be the coordinates of these red points (dashed lines for illustration purposes only):

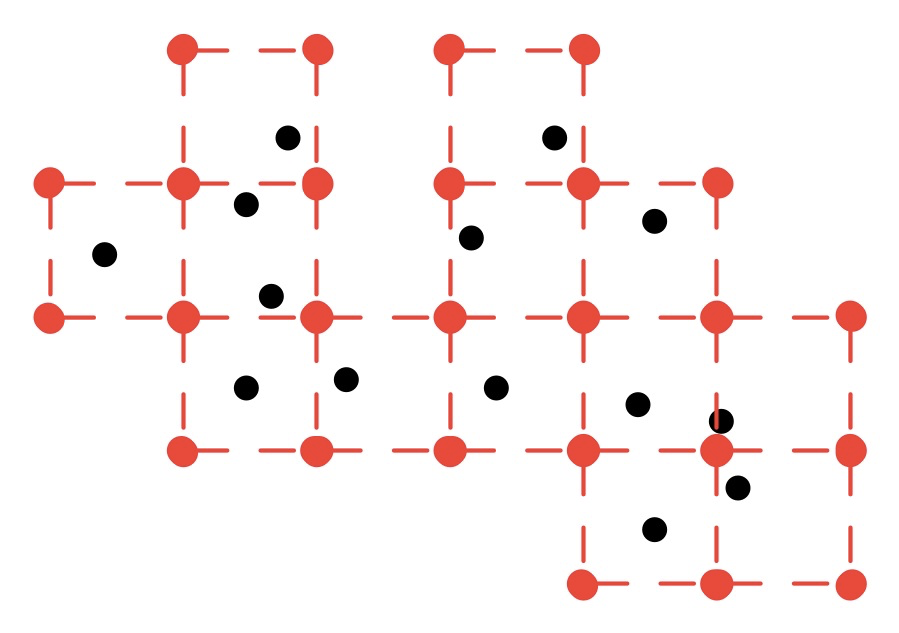
and for grid spacing X/2, one possible return value of the algorithm would be the coordinates of these red points (dashed lines for illustration purposes only):

For anyone who's interested, the disordered points that I'm working with are the atomic coordinates of large protein molecules, like what you can get out of a .pdb file.

Python is preferred for solutions, although pseudocode is also good.

EDIT: I think that my first description of what I needed was maybe a little fuzzy, so I added some constraints and images in order to clarify things.

Incipit

So would the minimal containing square be a valid solution, as it would contain at least one of the points and all of the points would be in it? i don't think so. – Ophthalmology

mostly importantly, what is the purpose of constructing the grid? – Prajna

Is the grid expected to be squares? Or could it be triangular or hex or rectangles or diamonds? Also, is the grid expected to be uniform, i.e. each cell in the grid is identical in nature (barring translation from origin) to each other cell in the grid? – Mirepoix

Can you say how this is to be used? For example, if it's for fast proximity checks there are several standard algorithms. – Brogan

By 'grid of minimum size', he actually means 'grid with minimum cell granularity'. Otherwise; yes, a bounding box for the entire point set would be the optimal solution. – Caliginous

@DanD. It would be a place to start :) But part of what I want is to be able to arbitrarily specify the spacing of the grid points. In other words, I want to be able to alter the density of the grid with a single variable. – Incipit

@DeepYellow The grid points are going to be used as probes in a calculation of the electrostatic field of the protein. Does that fall into "fast proximity checks"? I'm more of a physicist than a cs guy. – Incipit

@PengOne Your comment is both irrelevant and unhelpful. This is a question and answer site. You don't want to answer this particular question, go read another thread. – Incipit

@tel: yes, it does. You might look want to start here: en.wikipedia.org/wiki/Spatial_index#Spatial_Index. Blender already mentioned the k-d tree, but you should know about the other choices. – Brogan

Answer 1

Because you are asking for a regular square grid of user-specified spacing, it sounds like a reasonably straightforward approach should work.

Start by passing through the data to work out the minimum and maximum co-ordinate in each dimension. Work out the number of steps of user-specified spacing required to cover the distance between maximum and minimum.

Pass through the data again to allocate each point to a cell in the grid, using a grid with a point at the minimum of each co-ordinate and the specified spacing (e.g. X_cell = Math.floor((x_i - x_min) / spacing)). Use a dictionary or an array to record the number of points in each cell.

Now print out the co-ordinates of the cells with at least one point in them.

You do have some freedom that I have not attempted to optimise: unless the distance between minimum and maximum co-ordinate is an exact multiple of the grid spacing, there will be some slop that allows you to slide the grid around and still have it contain all the points: at the moment the grid starts at the position of the lowest point, but it probably ends before the highest points, so you have room to move it down a little in each dimension. As you do this, some points will move from cell to cell, and the number of occupied cells will change.

If you consider only moves in one dimension at a time, you can work out what will happen reasonably efficiently. Work out the distance in that dimension between each point and the maximum co-ordinate in that dimension of its cell, and then sort these values. As you move the grid down, the point with the smallest distance to its maximum co-ordinate will swap cells first, and you can iterate through these points one by one by moving through them in sorted order. If you update the counts of points in cells as you do this you can work out which shift minimises the number of occupied cells.

Of course, you have three dimensions to worry about. You could work on them one at a time until you getting reductions in the number of cells. This is a local minimum, but may not be a global minimum. One way to look for other local minima is to start again from a randomly chosen starting point.

Yettie

Answer 2

I'd suggest you make a k-d tree. It's fast-ish, simple, and easy to implement:

And Wikipedia code:

class Node: pass

def kdtree(point_list, depth=0):
    if not point_list:
        return

    # Select axis based on depth so that axis cycles through all valid values
    k = len(point_list[0]) # assumes all points have the same dimension
    axis = depth % k

    # Sort point list and choose median as pivot element
    point_list.sort(key=lambda point: point[axis])
    median = len(point_list) // 2 # choose median

    # Create node and construct subtrees
    node = Node()
    node.location = point_list[median]
    node.left_child = kdtree(point_list[:median], depth + 1)
    node.right_child = kdtree(point_list[median + 1:], depth + 1)
    return node

You'd have to slightly modify it, though, to fit within your constraints.

Brownstone

Answer 3

How about Voronoi Diagram? It can be generated in O(n log n) using Fortunes algorithm.

I don't know if it addresses your problem, but Voronoi Diagrams are very "narural". They are very common in the nature.

Example (from Wikipedia):

Alphorn

To anyone thinking about perpetrating another implementation on the world: the divide and conquer algorithms for Voronoi/Delaunay are much saner than Fortune's. Both have serious issues with nearly degenerate floating-point inputs. – Decennary

@Jimmy: Thanks - fixed that. It was from other question. – Doronicum

Answer 4

Find a minimum-area square that encloses all of the points. Repeatedly subdivide each square into 4 sub-squares (so going from 1 to 4 to 16 to 64 to …). Stop just before one of the squares becomes empty. It's not hard to prove that the resulting grid is at most four times as coarse as the optimal solution (key insight: an empty square is guaranteed to contain at least one square from any grid at least twice as fine).

Probably that constant can be reduced by introducing a random translation.

Decennary

Answer 5

I have experience with grid clustering in 2D and implemented an example in C# code. http://kunuk.wordpress.com/2011/09/15/clustering-grid-cluster/

This can handle step handle step 1, 2 and 4. You will have to modify the code and update it to 3D-space. Hope this gives you some ideas.

The code runs in O(m*n) where m is number of grids and n is number of points.

Noseband

Answer 6

If you want the grid cells to be square and regular, you most likely want an Octree. If you can relax the square and regular constraint, you can make a k-d-tree.

Sputum