Python fractal box count - fractal dimension

Question

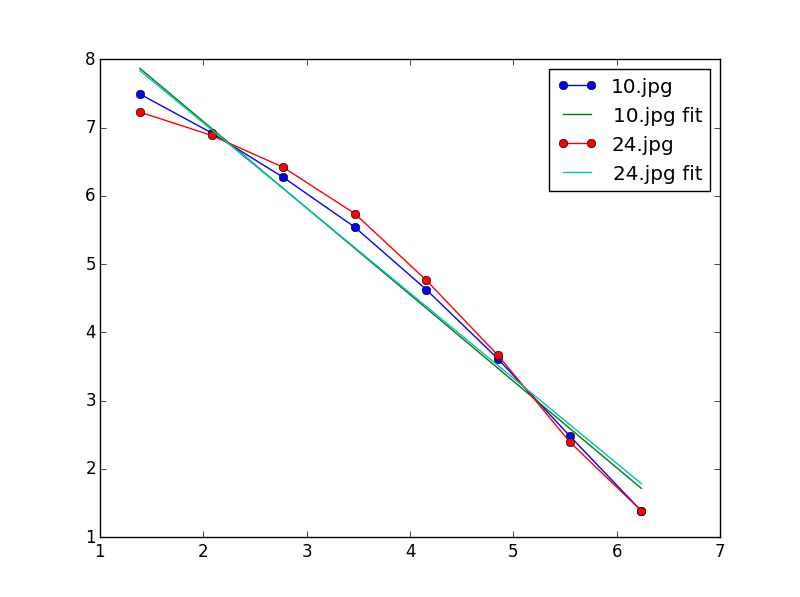
I have some images for which I want to calculate the Minkowski/box count dimension to determine the fractal characteristics in the image. Here are 2 example images:

10.jpg:

24.jpg:

I'm using the following code to calculate the fractal dimension:

import numpy as np
import scipy

def rgb2gray(rgb):
    r, g, b = rgb[:,:,0], rgb[:,:,1], rgb[:,:,2]
    gray = 0.2989 * r + 0.5870 * g + 0.1140 * b
    return gray

def fractal_dimension(Z, threshold=0.9):
    # Only for 2d image
    assert(len(Z.shape) == 2)

    # From https://github.com/rougier/numpy-100 (#87)
    def boxcount(Z, k):
        S = np.add.reduceat(
            np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
                               np.arange(0, Z.shape[1], k), axis=1)

        # We count non-empty (0) and non-full boxes (k*k)
        return len(np.where((S > 0) & (S < k*k))[0])

    # Transform Z into a binary array
    Z = (Z < threshold)

    # Minimal dimension of image
    p = min(Z.shape)

    # Greatest power of 2 less than or equal to p
    n = 2**np.floor(np.log(p)/np.log(2))

    # Extract the exponent
    n = int(np.log(n)/np.log(2))

    # Build successive box sizes (from 2**n down to 2**1)
    sizes = 2**np.arange(n, 1, -1)

    # Actual box counting with decreasing size
    counts = []
    for size in sizes:
        counts.append(boxcount(Z, size))

    # Fit the successive log(sizes) with log (counts)
    coeffs = np.polyfit(np.log(sizes), np.log(counts), 1)
    return -coeffs[0]

I = rgb2gray(scipy.misc.imread("24.jpg"))
print("Minkowski–Bouligand dimension (computed): ", fractal_dimension(I))

From the literature I've read, it has been suggested that natural scenes (e.g. 24.jpg) are more fractal in nature, and thus should have a larger fractal dimension value

The results it gives me are in the opposite direction than what the literature would suggest:

• 10.jpg: 1.259

• 24.jpg: 1.073

I would expect the fractal dimension for the natural image to be larger than for the urban

Am I calculating the value incorrectly in my code? Or am I just interpreting the results incorrectly?

Flume

This technique worked well for me, where I replaced the rgb2gray function with another (which preprocessed the image and focussed on a region with similar character) – Auditory

Inverting the threshold seems to produce nearly the same results (difference at the second decimal place, for my images; this seems incorrect (should be a larger difference). Have you tried this script with images of known Minkowski–Bouligand dimension? – Auditory

Answer 1

With fractal dimension of something physical the dimension might converge at different stages to different values. For example, a very thin line (but of finite width) would initially seem one dimensional, then eventual two dimensional as its width becomes of comparable size to the boxes used.

Lets see the dimensions that you have produced:

What do you see? Well the linear fits are not so good. And the dimensions is going towards a value of two. To diagnose, lets take a look at the grey-scale images produced, with the threshold that you have (that is, 0.9):

The nature picture has almost become an ink blob. The dimensions would go to a value of 2 very soon, as the graphs told us. That is because we pretty much lost the image. And now with a threshold of 50?

With new linear fits that are much better, the dimensions are 1.6 and 1.8 for urban and nature respectively. Keep in mind, that the urban picture actually has a lot of structure to it, in particular on the textured walls.

In future good threshold values would be ones closer to the mean of the grey scale images, that way your image does not turn into a blob of ink!

A good text book on this is "Fractals everywhere" by Michael F. Barnsley.

Scalage

Ah I didnt think to correct the threshold value. Would you advise I dynamically set the value of threshold to mean(Z) separately for each image? Or should the same threshold be used for all images if I wanted to compare the image values against each other? – Flume

The threshold helps you turn the image into a compact subset of the two dimensional 'canvas'. The threshold determines when a pixel is in the subset or not. Dynamically setting the threshold is a different comparison to fixing it. When it is dynamic, dark images and lighter ones are compared relative to their own lighting, but then an image of a dense bush might not be of higher dimension to a dead tree, or a wall. The dense tree image might come out almost two dimensional, like a giant ink blot. – Scalage

But dynamically setting a threshold means you can bring out the structure in the image regardless of its lighting conditions. So if you have a bank of images where you can't guarantee the same light levels, isn't it preferable to set the threshold dynamically so you know all images are treated equally (i.e. create a subset of pixels for each image that do not depend on things like the lighting condition)? I guess I'm having a hard time visualizing why dynamic threshold might be a bad thing – Flume

An example: A photo of the top of a dark bush and some empty bright sky. The sky clearly has a much lower dimension than the bush, if both are treated with the same threshold and we consider dark pixels as belonging to the fractal. But if you split the image up into two, and analyse them separately you will get a nearly dimension 2 for the sky, and something much less for the bush. In such cases it might be better to use the same threshold. It just depends on your comparison, dynamic threshold might invent structure you didn't want :) – Scalage

I don't understand why the fractal dimension would be close to 2 for the ink blob, doesn't 2 indicate the maximum possible complexity? – Annabelannabela