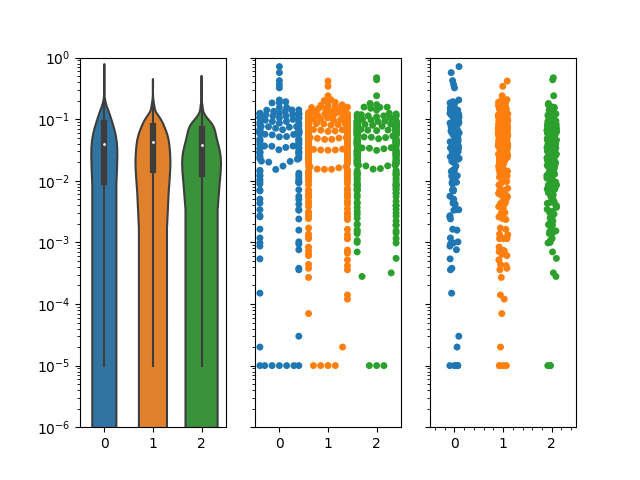
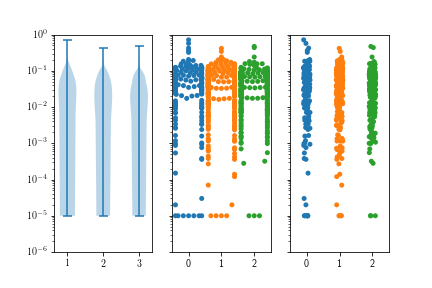
My violin plots are showing weird formats when using a log scale on my plots. I've tried using matplotlib and seaborn and I get very similar results.
import matplotlib.pyplot as plt
import seaborn as sns
data = [[1e-05, 0.00102, 0.00498, 0.09154, 0.02009, 1e-05, 0.06649, 0.42253, 0.02062, 0.10812, 0.07128, 0.03903, 0.00506, 0.13391, 0.08668, 0.04127, 0.00927, 0.00118, 0.063, 0.18392, 0.05948, 0.07774, 0.14018, 0.0133, 0.00339, 0.00271, 0.05233, 0.00054, 0.0593, 1e-05, 0.00076, 0.03409, 0.71491, 0.02311, 0.10246, 0.12491, 0.05164, 0.1553, 0.01079, 0.01734, 0.02239, 0.1347, 0.02877, 0.04752, 0.00333, 0.04553, 0.03189, 0.00947, 0.00158, 0.00888, 0.12663, 0.07531, 0.12367, 0.11346, 0.06638, 0.06154, 1e-05, 0.1838, 0.08659, 0.05654, 0.07658, 0.0348, 0.02954, 0.0123, 0.01529, 0.05559, 0.00416, 0.00038, 0.14142, 0.00164, 0.03671, 0.10609, 0.01209, 0.0024, 0.11718, 0.11224, 0.06032, 0.09632, 0.12216, 0.00087, 0.06746, 0.00433, 0.06836, 0.09928, 2e-05, 0.14116, 0.05718, 0.01196, 0.04297, 0.00709, 0.10535, 0.04772, 0.05691, 0.06277, 1e-05, 0.03917, 0.0026, 0.06763, 0.02083, 0.32244, 0.00561, 0.03399, 0.08146, 0.10606, 0.01482, 0.00339, 0.02275, 0.00685, 0.1536, 0.0592, 0.08869, 1e-05, 0.20489, 0.00094, 0.00714, 0.06355, 0.03414, 0.03002, 0.02365, 0.04376, 0.0246, 0.02745, 0.07604, 0.12069, 1e-05, 0.02974, 0.10681, 0.00987, 0.02543, 0.01416, 0.00098, 3e-05, 0.00967, 0.11958, 0.02882, 0.03634, 0.19232, 0.12058, 0.36535, 0.07428, 0.02829, 0.09189, 0.03677, 0.00036, 0.0463, 0.57029, 0.0105, 0.00015, 0.06212, 0.0329, 0.06102, 0.12267],
[0.01219, 0.14638, 0.03822, 0.05784, 0.03615, 0.03288, 0.00986, 0.05331, 0.01434, 0.00999, 0.05272, 0.03269, 0.0682, 0.15455, 0.09675, 0.02272, 0.0027, 0.01955, 0.06194, 0.00115, 0.07799, 0.03987, 0.11152, 0.07229, 0.007, 0.00075, 0.04499, 0.01534, 0.04301, 0.01247, 0.09511, 0.02297, 0.05538, 0.04614, 0.07359, 0.06909, 1e-05, 0.04247, 0.05485, 0.00071, 0.082, 0.07614, 0.03751, 0.01625, 0.03309, 0.03228, 0.08109, 0.02171, 0.07246, 0.00353, 0.02434, 0.01394, 0.037, 0.02429, 0.15162, 0.0527, 0.0201, 0.07954, 0.07626, 0.09285, 0.05071, 0.01224, 0.06331, 0.07556, 0.04952, 0.00052, 0.00588, 0.132, 0.00067, 0.00012, 0.00084, 0.03865, 0.02362, 0.08976, 0.18545, 0.04882, 0.03789, 0.05006, 0.02979, 0.003, 0.09262, 0.05668, 0.02486, 0.05855, 0.11588, 0.07713, 0.10428, 0.00706, 0.02467, 0.13257, 0.11547, 0.06143, 0.09478, 0.06099, 0.02483, 0.09312, 0.16867, 0.07236, 0.10962, 0.04149, 0.05005, 0.09087, 0.0313, 0.03697, 0.07201, 2e-05, 0.00259, 0.00115, 0.03907, 0.02931, 0.14907, 0.05598, 0.07087, 0.09709, 0.10653, 0.11936, 0.08196, 0.1213, 0.00627, 0.08496, 0.00038, 0.03537, 0.20043, 0.05159, 0.05872, 0.07754, 0.07621, 0.05924, 0.09587, 0.02653, 0.07135, 1e-05, 0.01377, 0.0062, 0.01965, 0.00115, 0.07529, 0.04709, 0.05458, 0.10895, 0.02195, 0.04534, 0.015, 0.00577, 0.05784, 0.01691, 0.08103, 0.04178, 0.04328, 0.01204, 0.03463, 0.03805, 0.01231, 0.03646, 0.01162, 0.16536, 0.03471, 0.00541, 0.09088, 0.06447, 0.07263, 0.05924, 0.0952, 0.09938, 0.04464, 0.05543, 0.03827, 0.11514, 0.02803, 0.09589, 0.0254, 0.05351, 0.00171, 0.00856, 0.05828, 0.11975, 7e-05, 0.07093, 0.06077, 0.0384, 0.00163, 0.05992, 0.00463, 0.00975, 0.00429, 0.12965, 0.03388, 0.02372, 0.07622, 0.04341, 0.06637, 0.00578, 0.06946, 0.00469, 0.11668, 0.07033, 0.06806, 0.05505, 0.02195, 0.05089, 0.03404, 0.00552, 0.05331, 0.03695, 0.41581, 0.01553, 0.02045, 0.09779, 0.03842, 0.01115, 0.05392, 0.01147, 0.05855, 0.05588, 0.20745, 0.01536, 0.03993, 0.07677, 0.01388, 0.0029, 0.00235, 0.05823, 0.05237, 0.00425, 0.09225, 0.00703, 0.24038, 0.06733, 0.00064, 0.08959, 0.04365, 0.02308, 0.04566, 0.08395, 0.0038, 0.05322, 0.0145, 0.02012, 0.07084, 0.08202, 0.01091, 0.03738, 0.03798, 0.03473, 0.08534, 0.00133, 0.04046, 0.10119, 0.0317, 0.00312, 0.03614, 0.10442, 0.13286, 0.0042, 0.04229, 0.01735, 0.09879, 0.07516, 0.00303, 0.08062, 0.09347, 0.03473, 0.05099, 0.16373, 0.08988, 0.04696, 0.07488, 0.12159, 0.11098, 0.00549, 0.00122, 0.05276, 0.09883, 0.01346, 0.02059, 0.07394, 0.0413, 0.08766, 0.0124, 0.09913, 0.00754, 0.15671, 0.02699, 0.09978, 1e-05, 0.00243, 0.02819, 0.00027, 0.05793, 0.03165, 0.10168, 0.00042, 0.00044, 0.01332, 0.00542, 0.05946, 0.009, 0.10857, 0.01699, 1e-05, 0.00073, 0.10842, 0.17143, 0.00036, 0.00014, 0.10508, 0.01333, 0.34202, 0.12201, 0.04618, 0.02507, 0.02939, 0.03497, 0.01905, 0.00136, 0.02354, 0.00061, 0.08514, 0.14529, 0.04097, 0.12821, 0.18862],
[0.04683, 0.02943, 0.07885, 0.07846, 0.06855, 0.02815, 0.00792, 0.0826, 0.00554, 0.01041, 0.03957, 0.0126, 0.08399, 0.15046, 0.15594, 0.03941, 0.0428, 0.11343, 0.15665, 0.07381, 0.04386, 0.12008, 0.04816, 0.04844, 0.08248, 0.08023, 0.03011, 0.00464, 0.07204, 0.08376, 0.05777, 0.06164, 0.00697, 0.02023, 0.04844, 0.0592, 0.00954, 0.06357, 0.0122, 0.05905, 0.00705, 0.0054, 0.08822, 0.06056, 0.02598, 0.02136, 0.05638, 0.03768, 0.05101, 0.08908, 0.0384, 0.01579, 0.04023, 0.03746, 0.17236, 0.08293, 0.12469, 0.14018, 0.04301, 0.07258, 0.02678, 0.08078, 0.07698, 0.06346, 0.06984, 0.04832, 0.07512, 0.0342, 0.05339, 0.026, 0.11585, 0.02744, 0.00979, 0.01312, 0.05915, 0.01326, 0.00107, 0.00737, 0.05971, 0.0451, 0.05788, 0.0007, 0.0043, 0.00142, 0.0019, 0.00055, 0.00223, 0.02441, 0.04555, 0.03869, 0.05791, 0.05517, 0.15743, 0.04517, 0.47114, 0.05639, 0.00152, 0.00371, 1e-05, 1e-05, 0.04192, 0.02758, 0.01945, 0.02763, 0.04021, 0.02844, 0.01823, 0.10665, 0.02067, 0.05433, 0.05591, 0.00733, 0.00858, 0.01949, 0.06519, 0.07793, 0.00199, 0.09916, 0.08717, 0.06273, 0.09408, 0.00638, 0.00248, 0.08922, 0.09157, 0.03525, 0.01791, 0.06016, 0.01939, 0.12194, 0.08303, 0.0831, 0.02714, 0.06312, 0.11584, 0.11334, 0.04314, 0.02575, 0.00629, 0.02408, 0.02274, 0.03037, 0.06737, 0.0175, 0.00888, 0.06568, 0.0839, 0.0085, 0.00831, 0.00154, 0.01072, 0.01289, 0.09074, 0.02131, 0.02997, 0.02343, 0.02355, 0.05324, 0.09564, 0.17995, 0.00828, 0.0148, 0.01858, 0.02106, 0.00288, 0.00344, 0.001, 0.02143, 0.00732, 0.01458, 0.01547, 0.01742, 0.00032, 0.24005, 0.00028, 0.00302, 0.07275, 0.04579, 0.06316, 0.02572, 0.09316, 0.03062, 0.10521, 0.07123, 0.03069, 0.07958, 0.04484, 0.01948, 0.01951, 0.01282, 0.00868, 0.07931, 0.01105, 0.01235, 0.09297, 0.06959, 0.00716, 0.0271, 0.00592, 0.09362, 0.00319, 0.00859, 0.08486, 0.02001, 0.00194, 0.04189, 0.09024, 0.07705, 0.07365, 0.01123, 0.03202, 0.01361, 0.00098, 0.00397, 0.00139, 0.00397, 0.00445, 1e-05, 0.00267, 0.06564, 0.06567, 0.06566, 0.06566, 0.09249, 0.03475, 0.0338, 0.0664, 0.02986, 0.04024, 0.00835, 0.04304, 0.04081, 0.04534, 0.06636, 0.03312, 0.06175, 0.03117, 0.02243, 0.03454, 0.11135, 0.07016, 0.0681, 0.09716, 0.02589, 0.4367, 0.08293, 0.11834, 0.00191, 0.10913, 0.00159, 0.0638, 0.01808, 0.00116, 0.00911, 0.01408, 0.09179, 0.02122, 0.05026, 0.05144, 0.03169, 0.06674]]
fig, ax = plt.subplots(1,3, sharey=True)
sns.violinplot(data=data, ax=ax[0])
sns.swarmplot(data=data, ax=ax[1])
sns.stripplot(data=data, ax=ax[2])
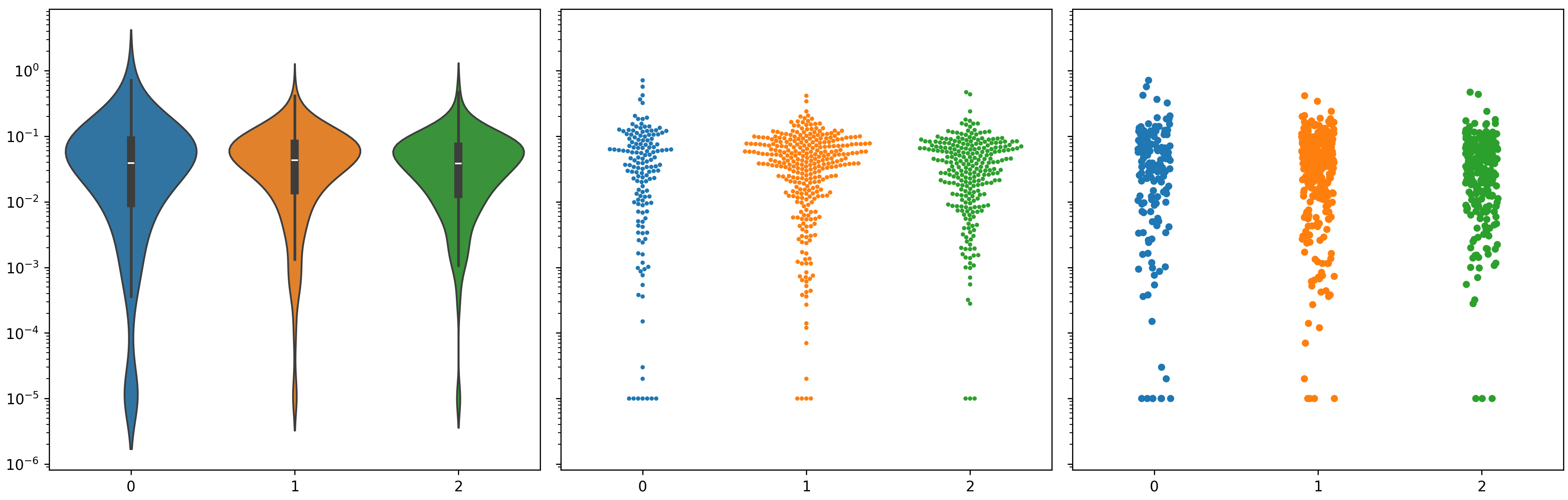
When using the data on a linear scale, everything looks fine. 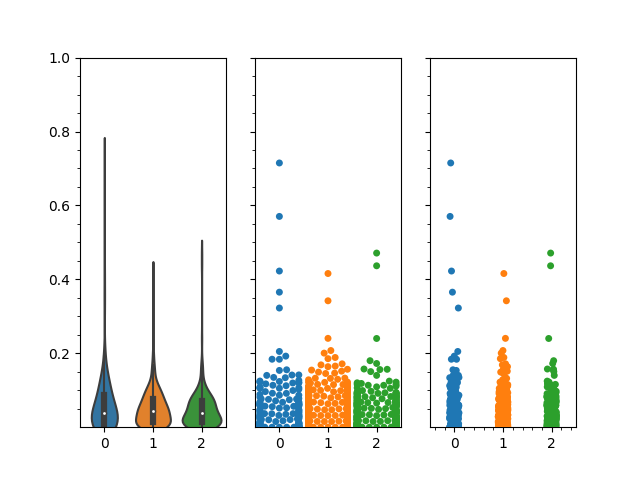 However, a lot of my data is between 0.1 and 0.00001 so I wanted to use a log scale for better visualization.
However, a lot of my data is between 0.1 and 0.00001 so I wanted to use a log scale for better visualization.
When switching to a log scale:
plt.yscale('log')
plt.ylim(0.000001, 1)
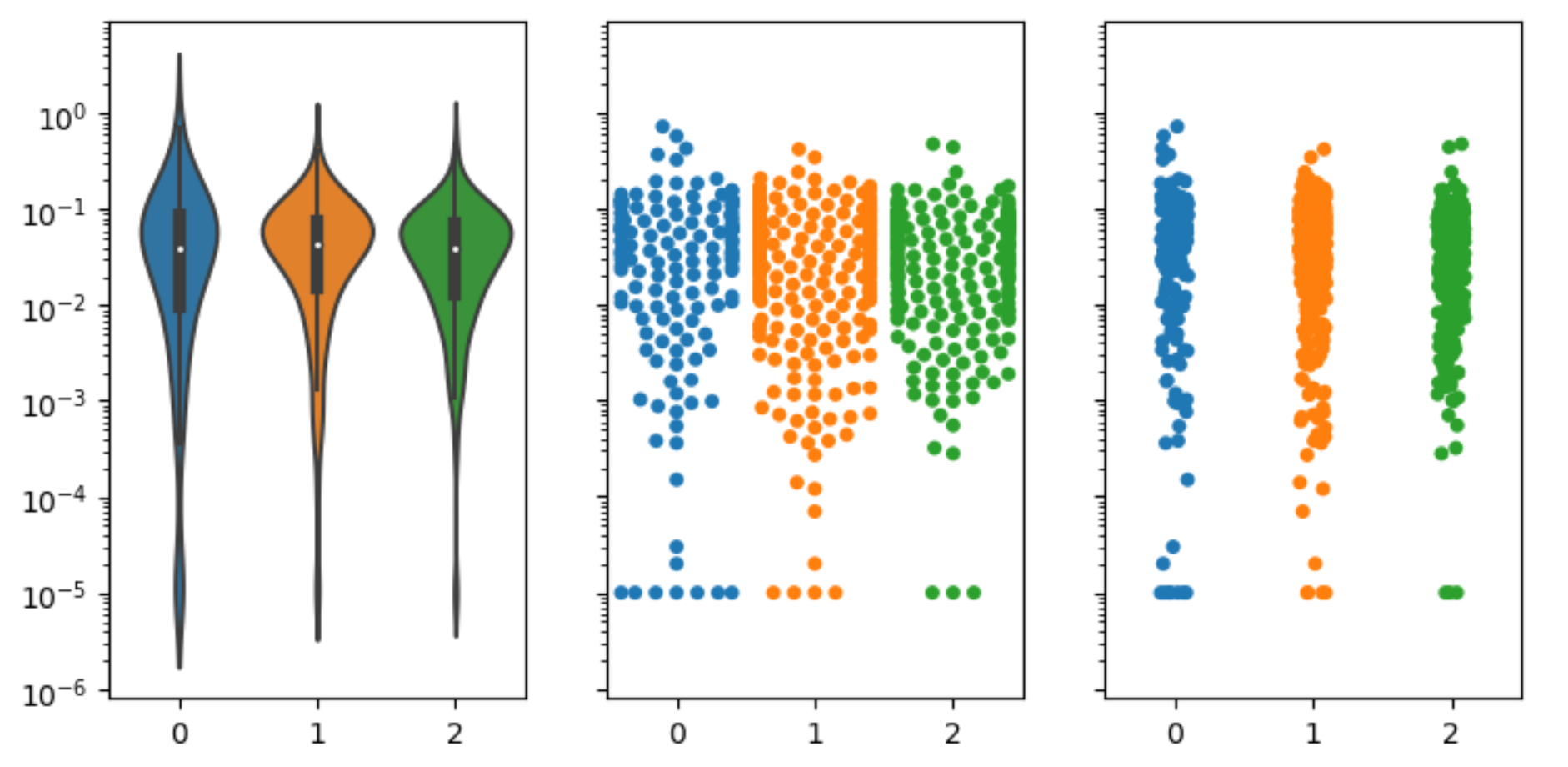
My swarmplot and stripplot plots look fine, however, the violin plots do not condense towards the bottom. Notice that I also don't have any negative values, but the violin plots always suggest that I do.
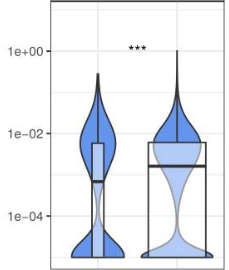
Overall, I would have expected my violin plots to look something more like this (which was done in R).
Any suggestions on how to get the violin plots to act more like the plots in the last picture (i.e. condensing when there are fewer data points) using seaborn or matplotlib, or another python based visualization?