Find the intersection between line and grid in a fast manner

Question

Is there anyway that allows me to find all the intersection points between a line and a grid? ( The intersection circles are not drawn to scale with each other, I know)

A brute force way is to compute very intersection for the x-y grid with the line, but this algorithm is awfully inefficient (O(m*n), where m is the number of x grid and n is the number of y grid).

I'm looking for a better algorithm on this.

Naranjo

Is the grid supposed to be regular? – Ctenoid

@Ignacio, yes the grid is regular. – Naranjo

Answer 1

Sounds like you need a Digital Differential Analyzer or Bresenham's line algorithm. Bresenham is the same algorithm used to draw lines on a bitmap; in this case, coloring a pixel is equivalent to checking for collisions in that square.

Lariat

I believe this should be the accepted answer. Using an algorithm like Bresenham's will give the grid points to check, and then from there individual intersection points can be calculated with much more ease - The horizontal and vertical components are all known. – Henrietta

Answer 2

I'm not sure I really understand the question. Is this what you're looking for by any chance?

Lamar

I want every single intersection point between the red line and the grid line. So, the points are (0,b), ((h-b)/m, h), (w, mw+b), (2w, 2wm+b), ((2h-b)/m,2h), (3w, 3wm+b) and so on – Naranjo

@dtb, nothing missing. But I want an efficient algorithm for that – Naranjo

This looks like one calculation per intersection to me. I can't imagine anything more efficient than that. – Lamar

@dtb, if that were the case, that would be awfully inefficient. Consider that you have a 100*100 grid, then you have to do at 100*100 operation. – Naranjo

@Ngu Soon Hui: I don't understand. The grid in my answer is made up of 5 horizontal and 5 vertical lines. The red line intersects with the grid lines at 7 places. To find these 7 intersections, you need to perform at most 10 calculations, not 25. – Lamar

@dtb, Ah, OK, you are right. But is there no other way to further optimize the thing? – Naranjo

@Ngu Soon Hui: You can stop when you get the first intersection outside the grid. Alternatively, since all intersections with horizontal grid lines and all intersections with vertical grid lines are equidistant respectively, you can simply calculate the first intersection respectively and get the other intersections by adding the delta repeatedly. Either way requires 9 calculations for the example in my answer. – Lamar

Answer 3

If the grid is axis aligned:

1. find out the line equation
2. calculate the intersection points directly using either the grid line's x or y as a fixed variable

If the grid is regular, the distance between the intersections with each horizontal line will be the same. The same also goes for the vertical lines. You could just do a simple iterative algorithm with dx and dy in that case.

Overalls

Answer 4

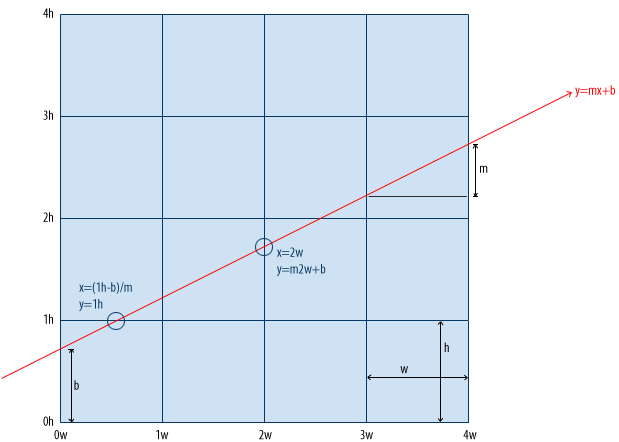
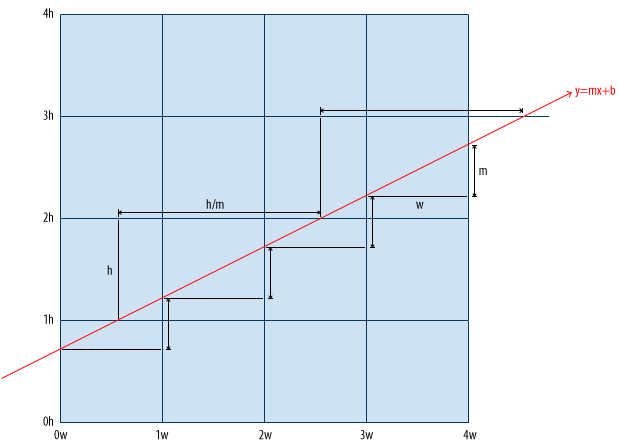
Algorithm:

The grid consists out of walls.

A wall is of/in a certain dimension: (Vertical, Horizontal, Depth)

The wall dimensions intersect forming cells (in final dimension)

The line intersects the walls primarly in their own dimension.

The solution is to view the problem as: How to intersect a line with a wall in it's own dimension.

The solution is to slide across the line from wall to wall, switch dimensions as necessary.

The sliding across the line happens such that the nearest wall is always chosen as the next destination.

The sliding from wall to wall in it's own dimension is constant/always the same.

The intersection of the line and the walls is different per dimension.

This ultimately decides the order of the wall intersections.

The solution is therefore to:

Phase 1: Initialization

Compute Dimension.IntersectT

Compute Dimension.SlideT

Phase 2: Start sliding from origin towards destination selecting nearest wall:

Dimension.T := Dimension.IntersectT

while ? end condition ?

Select smallest Dimension.T

Update selected Dimension.T += Dimension.SlideT

end

The difficulty lies in computing the Ts.

Bye, Skybuck.

Parmesan