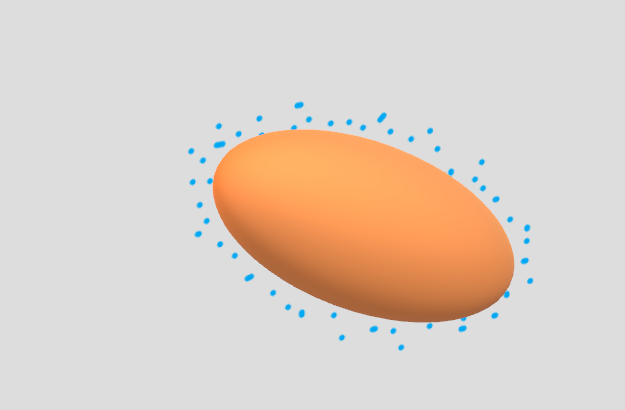
Problem statement
Given a number of points v₁, v₂, ..., vₙ, find a large ellipsoid satisfying two constraints:
- The ellipsoid is in the convex hull ℋ = ConvexHull(v₁, v₂, ..., vₙ).
- None of the points v₁, v₂, ..., vₙ is within the ellipsoid.
I propose an iterative procedure to find a large ellipsoid satisfying these two constraints. In each iteration we need to solve a semidefinite programming problem. This iterative procedure is guaranteed to converge, however it not guaranteed to converge to the globally largest ellipsoid.
Approach
Find a single ellipsoid
The core of our iterative procedure is that in each iteration, we find an ellipsoid satisfying 3 conditions:
- The ellipsoid is contained within ConvexHull(v₁, v₂, ..., vₙ) = {x | Ax<=b}.
- For a set of points u₁, ... uₘ (where {v₁, v₂, ..., vₙ} ⊂ {u₁, ... uₘ}, namely the given point in the point clouds belongs to this set of points u₁, ... uₘ), the ellipsoid doesn't contain any point in u₁, ... uₘ. We call this set u₁, ... uₘ as "outside points".
- For a set of points w₁,..., wₖ (where {w₁,..., wₖ} ∩ {v₁, v₂, ..., vₙ} = ∅, namely none of the point in v₁, v₂, ..., vₙ belongs to {w₁,..., wₖ}), the ellipsoid contains all of the points w₁,..., wₖ. We call this set w₁,..., wₖ as "inside points".
The intuitive idea is that the "inside points" w₁,..., wₖ indicate the volume of the ellipsoid. We will append new point to "inside points" so as to increase the ellipsoid volume.
To find such an ellipsoid through convex optimization, we parameterize the ellipsoid as
{x | xᵀPx + 2qᵀx ≤ r}
and we will search for P, q, r.
The condition that the "outside points" u₁, ... uₘ are all outside of the ellipsoid is formulated as
uᵢᵀPuᵢ + 2qᵀuᵢ >= r ∀ i=1, ..., m
this is a linear constraint on P, q, r.
The condition that the "inside points" w₁,..., wₖ are all inside the ellipsoid is formulated as
wᵢᵀPwᵢ + 2qᵀwᵢ <= r ∀ i=1, ..., k
This is also a linear constraint on P, q, r.
We also impose the constraint
P is positive definite
P being positive definite, together with the constraint that there exists points wᵢ satisfying wᵢᵀPwᵢ + 2qᵀwᵢ <= r guarantees that the set {x | xᵀPx + 2qᵀx ≤ r} is an ellipsoid.
We also have the constraint that the ellipsoid is inside the convex hull ℋ={x | aᵢᵀx≤ bᵢ, i=1,...,l} (namely there are l halfspaces as the H-representation of ℋ). Using s-lemma, we know that a necessary and sufficient condition for the halfspace {x|aᵢᵀx≤ bᵢ} containing the ellipsoid is that
∃ λᵢ >= 0,
s.t [P q -λᵢaᵢ/2] is positive semidefinite.
[(q-λᵢaᵢ/2)ᵀ λᵢbᵢ-r]
Hence we can solve the following semidefinite programming problem to find the ellipsoid that contains all the "inside points", doesn't contain any "outside points", and is within the convex hull ℋ
find P, q, r, λ
s.t uᵢᵀPuᵢ + 2qᵀuᵢ >= r ∀ i=1, ..., m
wᵢᵀPwᵢ + 2qᵀwᵢ <= r ∀ i=1, ..., k
P is positive definite.
λ >= 0,
[P q -λᵢaᵢ/2] is positive semidefinite.
[(q-λᵢaᵢ/2)ᵀ λᵢbᵢ-r]
We call this P, q, r = find_ellipsoid(outside_points, inside_points, A, b).
The volume of this ellipsoid is proportional to (r + qᵀP⁻¹q)/power(det(P), 1/3).
Iterative procedure.
We initialize "outside points" as all the points v₁, v₂, ..., vₙ in the point cloud, and "inside points" as a single point w₁ in the convex hull ℋ. In each iteration, we use find_ellipsoid function in the previous sub-section to find the ellipsoid within ℋ that contains all "inside points" but doesn't contain any "outside points". Depending on the result of the SDP in find_ellipsoid, we do the following
- If the SDP is feasible. We then compare the newly found ellipsoid with the largest ellipsoid found so far. If this new ellipsoid is larger, then accept it as the largest ellipsoid found so far.
- If the SDP is infeasible, then we remove the last point in "inside points", add this point to "outside point".
In both cases, we then take a new sample point in the convex hull ℋ, add that sample point to "inside points", and then solve the SDP again.
The complete algorithm is as follows
- Initialize "outside points" to v₁, v₂, ..., vₙ, initialize "inside points" to a single random point in the convex hull ℋ.
- while iter < max_iterations:
- Solve the SDP
P, q, r = find_ellipsoid(outside_points, inside_points, A, b).
- If SDP is feasible and volume(Ellipsoid(P, q, r)) > largest_volume, set
P_best = P, q_best=q, r_best = r.
- If SDP is infeasible, pt = inside_points.pop_last(), outside_points.push_back(pt).
- Randomly sample a new point in ℋ, append the point to "inside points", iter += 1. Go to step 3.
Code
from scipy.spatial import ConvexHull, Delaunay
import scipy
import cvxpy as cp
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import dirichlet
from mpl_toolkits.mplot3d import Axes3D # noqa
def get_hull(pts):
dim = pts.shape[1]
hull = ConvexHull(pts)
A = hull.equations[:, 0:dim]
b = hull.equations[:, dim]
return A, -b, hull
def compute_ellipsoid_volume(P, q, r):
"""
The volume of the ellipsoid xᵀPx + 2qᵀx ≤ r is proportional to
power(r + qᵀP⁻¹q, dim/2)/sqrt(det(P))
We return this number.
"""
dim = P.shape[0]
return np.power(r + q @ np.linalg.solve(P, q)), dim/2) / \
np.sqrt(np.linalg.det(P))
def uniform_sample_from_convex_hull(deln, dim, n):
"""
Uniformly sample n points in the convex hull Ax<=b
This is copied from
https://mcmap.net/q/1009000/-how-to-get-uniformly-distributed-points-in-convex-hull
@param deln Delaunay of the convex hull.
"""
vols = np.abs(np.linalg.det(deln[:, :dim, :] - deln[:, dim:, :]))\
/ np.math.factorial(dim)
sample = np.random.choice(len(vols), size=n, p=vols / vols.sum())
return np.einsum('ijk, ij -> ik', deln[sample],
dirichlet.rvs([1]*(dim + 1), size=n))
def centered_sample_from_convex_hull(pts):
"""
Sample a random point z that is in the convex hull of the points
v₁, ..., vₙ. z = (w₁v₁ + ... + wₙvₙ) / (w₁ + ... + wₙ) where wᵢ are all
uniformly sampled from [0, 1]. Notice that by central limit theorem, the
distribution of this sample is centered around the convex hull center, and
also with small variance when the number of points are large.
"""
num_pts = pts.shape[0]
pts_weights = np.random.uniform(0, 1, num_pts)
z = (pts_weights @ pts) / np.sum(pts_weights)
return z
def find_ellipsoid(outside_pts, inside_pts, A, b):
"""
For a given sets of points v₁, ..., vₙ, find the ellipsoid satisfying
three constraints:
1. The ellipsoid is within the convex hull of these points.
2. The ellipsoid doesn't contain any of the points.
3. The ellipsoid contains all the points in @p inside_pts
This ellipsoid is parameterized as {x | xᵀPx + 2qᵀx ≤ r }.
We find this ellipsoid by solving a semidefinite programming problem.
@param outside_pts outside_pts[i, :] is the i'th point vᵢ. The point vᵢ
must be outside of the ellipsoid.
@param inside_pts inside_pts[i, :] is the i'th point that must be inside
the ellipsoid.
@param A, b The convex hull of v₁, ..., vₙ is Ax<=b
@return (P, q, r, λ) P, q, r are the parameterization of this ellipsoid. λ
is the slack variable used in constraining the ellipsoid inside the convex
hull Ax <= b. If the problem is infeasible, then returns
None, None, None, None
"""
assert(isinstance(outside_pts, np.ndarray))
(num_outside_pts, dim) = outside_pts.shape
assert(isinstance(inside_pts, np.ndarray))
assert(inside_pts.shape[1] == dim)
num_inside_pts = inside_pts.shape[0]
constraints = []
P = cp.Variable((dim, dim), symmetric=True)
q = cp.Variable(dim)
r = cp.Variable()
# Impose the constraint that v₁, ..., vₙ are all outside of the ellipsoid.
for i in range(num_outside_pts):
constraints.append(
outside_pts[i, :] @ (P @ outside_pts[i, :]) +
2 * q @ outside_pts[i, :] >= r)
# P is strictly positive definite.
epsilon = 1e-6
constraints.append(P - epsilon * np.eye(dim) >> 0)
# Add the constraint that the ellipsoid contains @p inside_pts.
for i in range(num_inside_pts):
constraints.append(
inside_pts[i, :] @ (P @ inside_pts[i, :]) +
2 * q @ inside_pts[i, :] <= r)
# Now add the constraint that the ellipsoid is in the convex hull Ax<=b.
# Using s-lemma, we know that the constraint is
# ∃ λᵢ > 0,
# s.t [P q -λᵢaᵢ/2] is positive semidefinite.
# [(q-λᵢaᵢ/2)ᵀ λᵢbᵢ-r]
num_faces = A.shape[0]
lambda_var = cp.Variable(num_faces)
constraints.append(lambda_var >= 0)
Q = [None] * num_faces
for i in range(num_faces):
Q[i] = cp.Variable((dim+1, dim+1), PSD=True)
constraints.append(Q[i][:dim, :dim] == P)
constraints.append(Q[i][:dim, dim] == q - lambda_var[i] * A[i, :]/2)
constraints.append(Q[i][-1, -1] == lambda_var[i] * b[i] - r)
prob = cp.Problem(cp.Minimize(0), constraints)
try:
prob.solve(verbose=False)
except cp.error.SolverError:
return None, None, None, None
if prob.status == 'optimal':
P_val = P.value
q_val = q.value
r_val = r.value
lambda_val = lambda_var.value
return P_val, q_val, r_val, lambda_val
else:
return None, None, None, None
def draw_ellipsoid(P, q, r, outside_pts, inside_pts):
"""
Draw an ellipsoid defined as {x | xᵀPx + 2qᵀx ≤ r }
This ellipsoid is equivalent to
|Lx + L⁻¹q| ≤ √(r + qᵀP⁻¹q)
where L is the symmetric matrix satisfying L * L = P
"""
fig = plt.figure()
dim = P.shape[0]
L = scipy.linalg.sqrtm(P)
radius = np.sqrt(r + q@(np.linalg.solve(P, q)))
if dim == 2:
# first compute the points on the unit sphere
theta = np.linspace(0, 2 * np.pi, 200)
sphere_pts = np.vstack((np.cos(theta), np.sin(theta)))
ellipsoid_pts = np.linalg.solve(
L, radius * sphere_pts - (np.linalg.solve(L, q)).reshape((2, -1)))
ax = fig.add_subplot(111)
ax.plot(ellipsoid_pts[0, :], ellipsoid_pts[1, :], c='blue')
ax.scatter(outside_pts[:, 0], outside_pts[:, 1], c='red')
ax.scatter(inside_pts[:, 0], inside_pts[:, 1], s=20, c='green')
ax.axis('equal')
plt.show()
if dim == 3:
u = np.linspace(0, np.pi, 30)
v = np.linspace(0, 2*np.pi, 30)
sphere_pts_x = np.outer(np.sin(u), np.sin(v))
sphere_pts_y = np.outer(np.sin(u), np.cos(v))
sphere_pts_z = np.outer(np.cos(u), np.ones_like(v))
sphere_pts = np.vstack((
sphere_pts_x.reshape((1, -1)), sphere_pts_y.reshape((1, -1)),
sphere_pts_z.reshape((1, -1))))
ellipsoid_pts = np.linalg.solve(
L, radius * sphere_pts - (np.linalg.solve(L, q)).reshape((3, -1)))
ax = plt.axes(projection='3d')
ellipsoid_pts_x = ellipsoid_pts[0, :].reshape(sphere_pts_x.shape)
ellipsoid_pts_y = ellipsoid_pts[1, :].reshape(sphere_pts_y.shape)
ellipsoid_pts_z = ellipsoid_pts[2, :].reshape(sphere_pts_z.shape)
ax.plot_wireframe(ellipsoid_pts_x, ellipsoid_pts_y, ellipsoid_pts_z)
ax.scatter(outside_pts[:, 0], outside_pts[:, 1], outside_pts[:, 2],
c='red')
ax.scatter(inside_pts[:, 0], inside_pts[:, 1], inside_pts[:, 2], s=20,
c='green')
ax.axis('equal')
plt.show()
def find_large_ellipsoid(pts, max_iterations):
"""
We find a large ellipsoid within the convex hull of @p pts but not
containing any point in @p pts.
The algorithm proceeds iteratively
1. Start with outside_pts = pts, inside_pts = z where z is a random point
in the convex hull of @p outside_pts.
2. while num_iter < max_iterations
3. Solve an SDP to find an ellipsoid that is within the convex hull of
@p pts, not containing any outside_pts, but contains all inside_pts.
4. If the SDP in the previous step is infeasible, then remove z from
inside_pts, and append it to the outside_pts.
5. Randomly sample a point in the convex hull of @p pts, if this point is
outside of the current ellipsoid, then append it to inside_pts.
6. num_iter += 1
When the iterations limit is reached, we report the ellipsoid with the
maximal volume.
@param pts pts[i, :] is the i'th points that has to be outside of the
ellipsoid.
@param max_iterations The iterations limit.
@return (P, q, r) The largest ellipsoid is parameterized as
{x | xᵀPx + 2qᵀx ≤ r }
"""
dim = pts.shape[1]
A, b, hull = get_hull(pts)
hull_vertices = pts[hull.vertices]
deln = hull_vertices[Delaunay(hull_vertices).simplices]
outside_pts = pts
z = centered_sample_from_convex_hull(pts)
inside_pts = z.reshape((1, -1))
num_iter = 0
max_ellipsoid_volume = -np.inf
while num_iter < max_iterations:
(P, q, r, lambda_val) = find_ellipsoid(outside_pts, inside_pts, A, b)
if P is not None:
volume = compute_ellipsoid_volume(P, q, r)
if volume > max_ellipsoid_volume:
max_ellipsoid_volume = volume
P_best = P
q_best = q
r_best = r
else:
# Adding the last inside_pts doesn't increase the ellipsoid
# volume, so remove it.
inside_pts = inside_pts[:-1, :]
else:
outside_pts = np.vstack((outside_pts, inside_pts[-1, :]))
inside_pts = inside_pts[:-1, :]
# Now take a new sample that is outside of the ellipsoid.
sample_pts = uniform_sample_from_convex_hull(deln, dim, 20)
is_in_ellipsoid = np.sum(sample_pts.T*(P_best @ sample_pts.T), axis=0)\
+ 2 * sample_pts @ q_best <= r_best
if np.all(is_in_ellipsoid):
# All the sampled points are in the ellipsoid, the ellipsoid is
# already large enough.
return P_best, q_best, r_best
else:
inside_pts = np.vstack((
inside_pts, sample_pts[np.where(~is_in_ellipsoid)[0][0], :]))
num_iter += 1
return P_best, q_best, r_best
if __name__ == "__main__":
pts = np.array([[0., 0.], [0., 1.], [1., 1.], [1., 0.], [0.2, 0.4]])
max_iterations = 10
P, q, r = find_large_ellipsoid(pts, max_iterations)
I also put the code in the github repo
Results
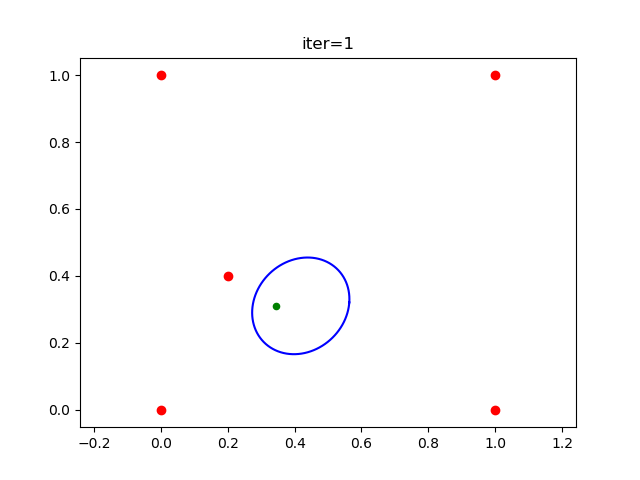
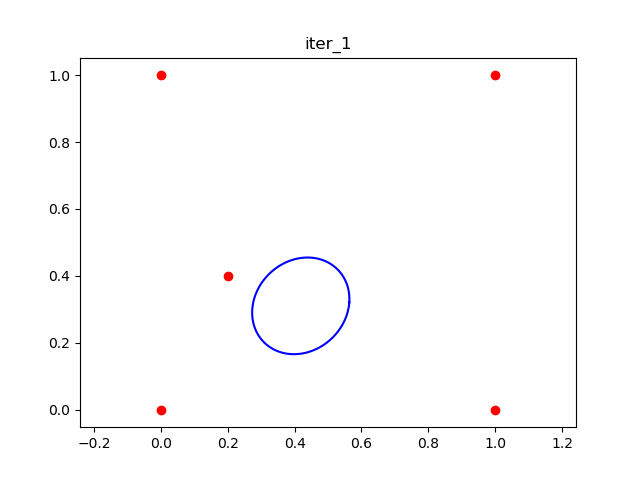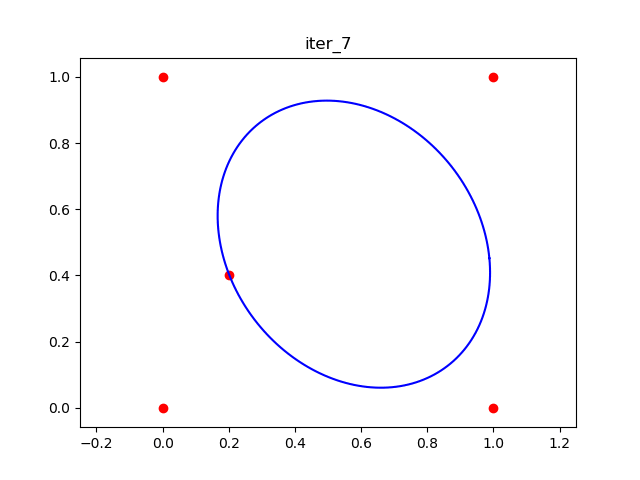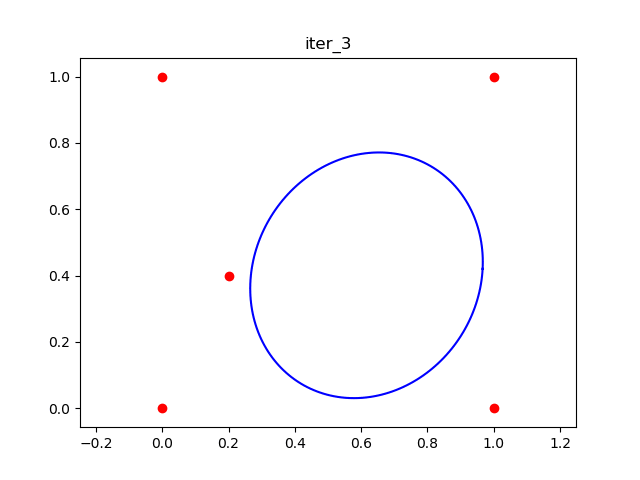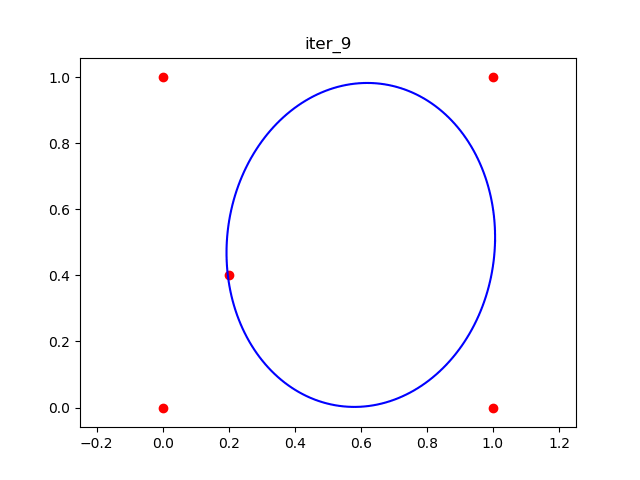
Here is the result on a simple 2D example, say we want to find a large ellipsoid that doesn't contain the five red points in the figure below. Here is the result after the first iteration
![iteration1_result]() . The red points are the "outside points" (the initial outside points are v₁, v₂, ..., vₙ), the green point is the initial "inside points".
. The red points are the "outside points" (the initial outside points are v₁, v₂, ..., vₙ), the green point is the initial "inside points".
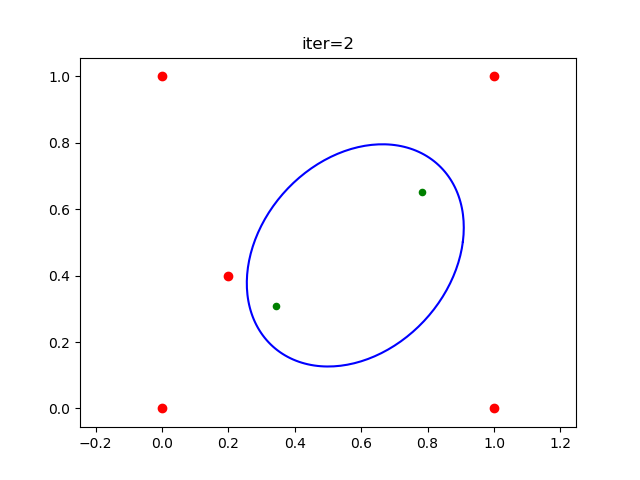
In the second iteration, the ellipsoid becomes
![iteration2_result]() . By adding one more "inside point" (green dot), the ellipsoid gets larger.
. By adding one more "inside point" (green dot), the ellipsoid gets larger.
This gif shows the animation of the 10 iteations.![all_iterations_result]()