Predict probabilities using SVM

Question

I wrote this code and wanted to obtain probabilities of classification.

from sklearn import svm
X = [[0, 0], [10, 10],[20,30],[30,30],[40, 30], [80,60], [80,50]]
y = [0, 1, 2, 3, 4, 5, 6]
clf = svm.SVC() 
clf.probability=True
clf.fit(X, y)
prob = clf.predict_proba([[10, 10]])
print prob

I obtained this output:

[[0.15376986 0.07691205 0.15388546 0.15389275 0.15386348 0.15383004 0.15384636]]

which is very weird because the probability should have been

[0 1 0 0 0 0 0 0]

(Observe that the sample for which class has to be predicted is same as 2nd sample) also, probability obtained for that class is the lowest.

Trici

probability should sum up to 1. It does not mean that they should be 0 or 1! You can use argmax to choose the highest probability. In your case, the probability of 6 classes is equal. Therefore, it can belong to any class but not class 1. – Ardithardme

Answer 1

EDIT: As pointed out by @TimH, the probablities can be given by clf.decision_function(X). The below code is fixed. Noting the appointed issue with low probabilities using predict_proba(X), I think the answer is that according to official doc here, .... Also, it will produce meaningless results on very small datasets.

The answer residue in understanding what the resulting probablities of SVMs are. In short, you have 7 classes and 7 points in the 2D plane. What SVMs are trying to do, is to find a linear separator, between each class and each one the others (one-vs-one approach). Every time only 2 classes are chosen. What you get is the votes of the classifiers, after normalization. See more detailed explanation on multi-class SVMs of libsvm in this post or here (scikit-learn uses libsvm).

By slightly modifying your code, we see that indeed the right class is chosen:

from sklearn import svm
import matplotlib.pyplot as plt
import numpy as np


X = [[0, 0], [10, 10],[20,30],[30,30],[40, 30], [80,60], [80,50]]
y = [0, 1, 2, 3, 3, 4, 4]
clf = svm.SVC() 
clf.fit(X, y)

x_pred = [[10,10]]
p = np.array(clf.decision_function(x_pred)) # decision is a voting function
prob = np.exp(p)/np.sum(np.exp(p),axis=1, keepdims=True) # softmax after the voting
classes = clf.predict(x_pred)

_ = [print('Sample={}, Prediction={},\n Votes={} \nP={}, '.format(idx,c,v, s)) for idx, (v,s,c) in enumerate(zip(p,prob,classes))]

The corresponding output is

Sample=0, Prediction=0,
Votes=[ 6.5         4.91666667  3.91666667  2.91666667  1.91666667  0.91666667 -0.08333333] 
P=[ 0.75531071  0.15505748  0.05704246  0.02098475  0.00771986  0.00283998  0.00104477], 
Sample=1, Prediction=1,
Votes=[ 4.91666667  6.5         3.91666667  2.91666667  1.91666667  0.91666667 -0.08333333] 
P=[ 0.15505748  0.75531071  0.05704246  0.02098475  0.00771986  0.00283998  0.00104477], 
Sample=2, Prediction=2,
Votes=[ 1.91666667  2.91666667  6.5         4.91666667  3.91666667  0.91666667 -0.08333333] 
P=[ 0.00771986  0.02098475  0.75531071  0.15505748  0.05704246  0.00283998  0.00104477], 
Sample=3, Prediction=3,
Votes=[ 1.91666667  2.91666667  4.91666667  6.5         3.91666667  0.91666667 -0.08333333] 
P=[ 0.00771986  0.02098475  0.15505748  0.75531071  0.05704246  0.00283998  0.00104477], 
Sample=4, Prediction=4,
Votes=[ 1.91666667  2.91666667  3.91666667  4.91666667  6.5         0.91666667 -0.08333333] 
P=[ 0.00771986  0.02098475  0.05704246  0.15505748  0.75531071  0.00283998  0.00104477], 
Sample=5, Prediction=5,
Votes=[ 3.91666667  2.91666667  1.91666667  0.91666667 -0.08333333  6.5  4.91666667] 
P=[ 0.05704246  0.02098475  0.00771986  0.00283998  0.00104477  0.75531071  0.15505748], 
Sample=6, Prediction=6,
Votes=[ 3.91666667  2.91666667  1.91666667  0.91666667 -0.08333333  4.91666667  6.5       ] 
P=[ 0.05704246  0.02098475  0.00771986  0.00283998  0.00104477  0.15505748  0.75531071], 

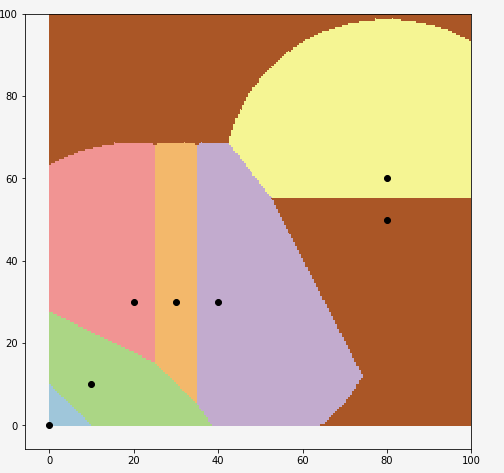
And you can also see decision zones:

X = np.array(X)
y = np.array(y)
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)

XX, YY = np.mgrid[0:100:200j, 0:100:200j]
Z = clf.predict(np.c_[XX.ravel(), YY.ravel()])

Z = Z.reshape(XX.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(XX, YY, Z, cmap=plt.cm.Paired)

for idx in range(7):
    ax.scatter(X[idx,0],X[idx,1], color='k')

Finnell

I think his major problem is to understand why the probability for the correct class is the smallest out of all. This question is not answered here – Phiphenomenon

@Phiphenomenon Thanks, added note on the probablities. – Finnell

@Finnell What tool /IDE did you use to obtain the plot..? I tried to run the code on Ubuntu terminal... it gave me the prediction but not the graph – Trici

I used matplotlib.pyplot. The example is self-contained, this is the code. – Finnell

@VidyaMarathe I used it within Jupyter, just add plt.show() to see the graph. – Finnell

I don't think that this answer is correct. What you refer to as probabilities are not really probabilities. In the documentation of decision_function, this post is mentioned where it is explained why. Similarly, in page 4 of this document it's also said that the mapping from decision functions to probabilities via softmax "is not very well founded". – Justiciary

In SVC(), the default value of decision_function_shape is ’ovr’, which means it returns a one-vs-rest (‘ovr’) decision function of shape (n_samples, n_classes) as all other classifiers. In this demo, the label space is [0, 1, 2, 3], so n_classes = 4. So why P contains 7 results ? Here is my results from sklearn=0.24.1: Sample=0, Prediction=0, Votes=[ 3.16124317 3.19468064 0.87106327 3.17454938 -0.24583347] P=[0.31428908 0.32497579 0.03182122 0.31849903 0.01041489], Thanks – Maryannamaryanne

@Maryannamaryanne Actually there are 5 classes. Regarding the P values, it is the number of samples and the "probability" for each one of them. – Finnell

Thanks for your timely reply @mr_mo. Yes. The label space is [0, 1, 2, 3, 4] and n_classes = 5. I suppose that replace x_pred = [[10,10]] with x_pred = X might be clear. It will match the outputs as shown : ) – Maryannamaryanne

Answer 2

You should disable probability and use decision_function instead, because there is no guarantee that predict_proba and predict return the same result. You can read more about it, here in the documentation.

clf.predict([[10, 10]]) // returns 1 as expected 

prop = clf.decision_function([[10, 10]]) // returns [[ 4.91666667  6.5         3.91666667  2.91666667  1.91666667  0.91666667
      -0.08333333]]
prediction = np.argmax(prop) // returns 1 

Trenna

your answer does not has fancy plots, but for me is the most useful one, I would only add that you can apply a softmax to the output of the decision_function to convert it to probabilities that is what the user requested add the beggining – Soupspoon

@Soupspoon thanks for your feedback. I would appreciate an upvote. – Trenna

upps, sorry, there you have it ! =D – Soupspoon

Answer 3

You can read in the docs that...

The SVC method decision_function gives per-class scores for each sample (or a single score per sample in the binary case). When the constructor option probability is set to True, class membership probability estimates (from the methods predict_proba and predict_log_proba) are enabled. In the binary case, the probabilities are calibrated using Platt scaling: logistic regression on the SVM’s scores, fit by an additional cross-validation on the training data. In the multiclass case, this is extended as per Wu et al. (2004).

Needless to say, the cross-validation involved in Platt scaling is an expensive operation for large datasets. In addition, the probability estimates may be inconsistent with the scores, in the sense that the “argmax” of the scores may not be the argmax of the probabilities. (E.g., in binary classification, a sample may be labeled by predict as belonging to a class that has probability <½ according to predict_proba.) Platt’s method is also known to have theoretical issues. If confidence scores are required, but these do not have to be probabilities, then it is advisable to set probability=False and use decision_function instead of predict_proba.

There are also lots of confusion about this function amongst Stack Overflow users, as you can see in this thread, or this one.

Uncle