Understanding the PyTorch implementation of Conv2DTranspose

Question

I am trying to understand an example snippet that makes use of the PyTorch transposed convolution function, with documentation here, where in the docs the author writes:

"The padding argument effectively adds dilation * (kernel_size - 1) - padding amount of zero padding to both sizes of the input."

Consider the snippet below where a sample image of shape [1, 1, 4, 4] containing all ones is input to a ConvTranspose2D operation with arguments stride=2 and padding=1 with a weight matrix of shape (1, 1, 4, 4) that has entries from a range between 1 and 16 (in this case dilation=1 and added_padding = 1*(4-1)-1 = 2)

sample_im = torch.ones(1, 1, 4, 4).cuda()
sample_deconv = nn.ConvTranspose2d(1, 1, 4, 2, 1, bias=False).cuda()
sample_deconv.weight = torch.nn.Parameter(
    torch.tensor([[[[ 1.,  2.,  3.,  4.], 
                    [ 5.,  6.,  7.,  8.], 
                    [ 9., 10., 11., 12.], 
                    [13., 14., 15., 16.]]]]).cuda())

Which yields:

>>> sample_deconv(sample_im)
tensor([[[[ 6., 12., 14., 12., 14., 12., 14.,  7.],
          [12., 24., 28., 24., 28., 24., 28., 14.],
          [20., 40., 44., 40., 44., 40., 44., 22.],
          [12., 24., 28., 24., 28., 24., 28., 14.],
          [20., 40., 44., 40., 44., 40., 44., 22.],
          [12., 24., 28., 24., 28., 24., 28., 14.],
          [20., 40., 44., 40., 44., 40., 44., 22.],
          [10., 20., 22., 20., 22., 20., 22., 11.]]]], device='cuda:0',
       grad_fn=<CudnnConvolutionTransposeBackward>)

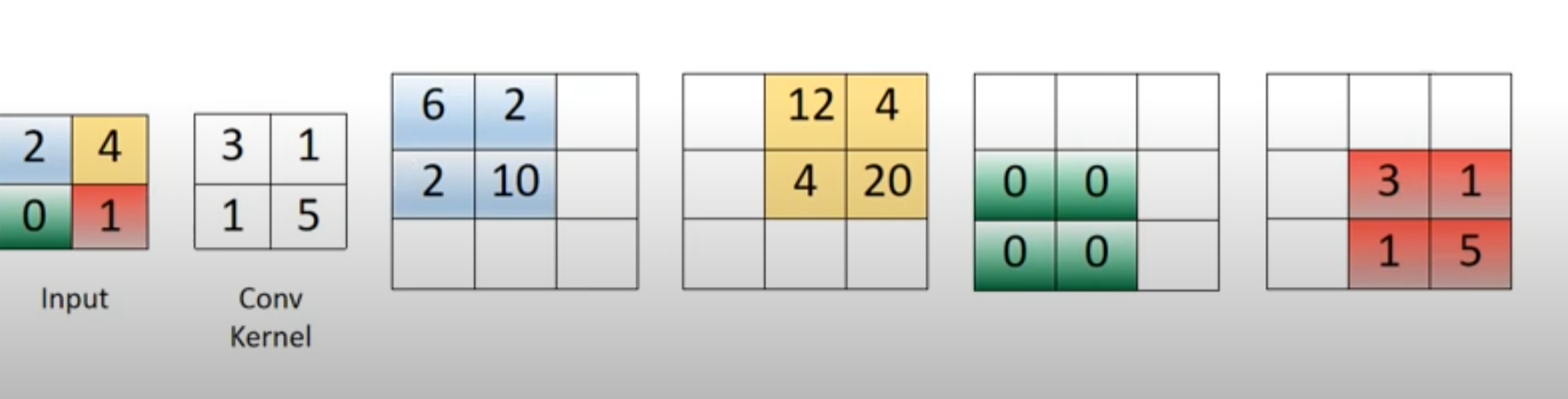
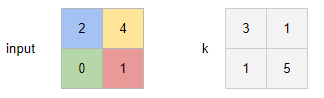
Now I have seen simple examples of transposed convolution without stride and padding. For instance, if the input is a 2x2 image [[2, 4], [0, 1]], and the convolutional filter with one output channel is [[3, 1], [1, 5]], then the resulting tensor of shape (1, 1, 3, 3) can be seen as the sum of the four colored matrices in the image below:

The problem is I can't seem to find examples that use strides and/or padding in the same visualization. As per my snippet, I am having a very difficult time understanding how the padding is applied to the sample image, or how the stride works to get this output. Any insights appreciated, even just understanding how the 6 in the (0,0) entry or the 12 in the (0,1) entry of the resulting matrix are computed would be very helpful.

Frump

Answer 1

The output spatial dimensions of nn.ConvTranspose2d are given by:

out = (x - 1)s - 2p + d(k - 1) + op + 1

where x is the input spatial dimension and out the corresponding output size, s is the stride, d the dilation, p the padding, k the kernel size, and op the output padding.

---

If we keep the following operands:

For each value of the input, we compute a buffer (of the corresponding color) by calculating the product with each element of the kernel.

Here are the visualizations for s=1, p=0, s=1, p=1, s=2, p=0, and s=2, p=1:

• s=1, p=0: output is 3x3

For the blue buffer, we have (1) 2*k_top-left = 2*3 = 6; (2) 2*k_top-right = 2*1 = 2; (3) 2*k_bottom-left = 2*1 = 2; (4) 2*k_bottom-right = 2*5 = 10.

• s=1, p=1: output is 1x1

• s=2, p=0: output is 4x4

• s=2, p=2: output is 2x2

Moat

Ok! I think the crux of my confusion is the what the $p$ argument does, If I understand correctly, its as if when p=1, you are removing one column and one row from each side of the four matrices that are being added? Almost like a kind of "anti" - padding Thanks a lot for the great answer, I hope this will be useful to someone else in the future. – Frump

Should it be s=2, p=1 in the last example? – Polychromy

Answer 2

I believe what makes things confusing is that they are not very careful about what they meant by "input" or "output" in the doc, and the overloading of the terms "stride" and "padding".

I found it easier to understand transposed convolution in PyTorch by asking myself: What arguments would I give to a normal, forward convolution layer such that it would give the tensor at hand, that I'm feeding into a transposed conv layer?

For instance, "stride" should be understood as the "stride" in a forward conv, i.e. the moving step of the sliding kernel.

In a transposed conv, "stride" actually means something different: stride-1 is the number of the interleaving empty slots in between the input units into the transposed conv layer. That's because it is the greater-than-1 "strides" in a forward conv that create such holes. See image below for an illustration:

The illustration also shows that the kernel moving step in a transposed conv layer is always 1, regardless of the value of "stride". I found it very important to keep this in mind.

Similar for the padding argument. It should be understood as the 0-padding applied to the forward conv. Because of this padding, we get some extra units in the output from the forward conv. So, if we then feed this output into a transposed conv, in order to get back to the original, non-padded length, those extra things should be removed, thus the -2p term in the equation.

See image below for an illustration.

In summary, these are designed as such that normal conv and transposed conv are "inverse" operations to each other, in the sense of tensor shape transformations. (But I do believe that the doc should be improved.)

With this principle in mind, one can also work out the dilation and output_padding arguments relatively easily. I've written a blog on this, in case anyone is interested.

Spindling