Peak of the kernel density estimation

Question

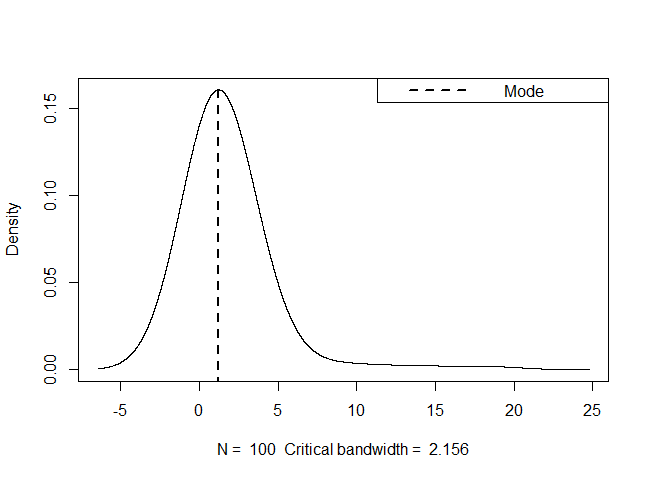
I need to find as precisely as possible the peak of the kernel density estimation (modal value of the continuous random variable). I can find the approximate value:

x<-rlnorm(100)
d<-density(x)
plot(d)
i<-which.max(d$y)
d$y[i]
d$x[i]

But when calculating d$y precise function is known. How can I locate the exact value of the mode?

Craggy

Answer 1

Here are two functions for dealing with modes. The dmode function finds the mode with the highest peak (dominate mode) and n.modes identify the number of modes.

    dmode <- function(x) {
      den <- density(x, kernel=c("gaussian"))
        ( den$x[den$y==max(den$y)] )   
    }  

    n.modes <- function(x) {  
       den <- density(x, kernel=c("gaussian"))
       den.s <- smooth.spline(den$x, den$y, all.knots=TRUE, spar=0.8)
         s.0 <- predict(den.s, den.s$x, deriv=0)
         s.1 <- predict(den.s, den.s$x, deriv=1)
       s.derv <- data.frame(s0=s.0$y, s1=s.1$y)
       nmodes <- length(rle(den.sign <- sign(s.derv$s1))$values)/2
       if ((nmodes > 10) == TRUE) { nmodes <- 10 }
          if (is.na(nmodes) == TRUE) { nmodes <- 0 } 
       ( nmodes )
    }

# Example
x <- runif(1000,0,100)
  plot(density(x))
    abline(v=dmode(x))

Galenical

Answer 2

If I understand your question, I think you are just wanting a finer discretisation of x and y. To do this, you can change the value of n in the density function (default is n=512).

For example, compare

set.seed(1)
x = rlnorm(100)
d = density(x)
i = which.max(d$y)
d$y[i]; d$x[i]
0.4526; 0.722

with:

d = density(x, n=1e6)
i = which.max(d$y)
d$y[i]; d$x[i]
0.4525; 0.7228

Lauren

Answer 3

I think you need two steps to archive what you need:

1) Find the x-Axis value of the KDE peak

2) Get the desnity value of the peak

So (if you dont mind using a package) a solution using the hdrcde package would look like this:

require(hdrcde)

x<-rlnorm(100)
d<-density(x)

# calcualte KDE with help of the hdrcde package
hdrResult<-hdr(den=d,prob=0)

# define the linear interpolation function for the density estimation
dd<-approxfun(d$x,d$y)
# get the density value of the KDE peak
vDens<-dd(hdrResult[['mode']])

Edit: You could also use the

hdrResult[['falpha']]

if it is precise enough for you!

Hardpan

Answer 4

A one-liner using the ‘multimode’ package:

multimode::locmodes(x)$locations[1]

Estimated location
Mode: 1.238839 

Estimated value of the density
Mode: 0.1605735 

Critical bandwidth: 2.155968

To also display the position of the calculated mode on a plot of the KDE, add the display = TRUE parameter.

multimode::locmodes(x, display = TRUE)

The position of multiple modes (and their antimodes)can be returned using the mod0 parameter; modes take the odd positions of locmodes(x)$locations, antimodes the even positions.

Burnish