Numbers of combinations modulo m, efficiently

Question

First of all I'm solving a programming problem rather than a math problem now.

The question is

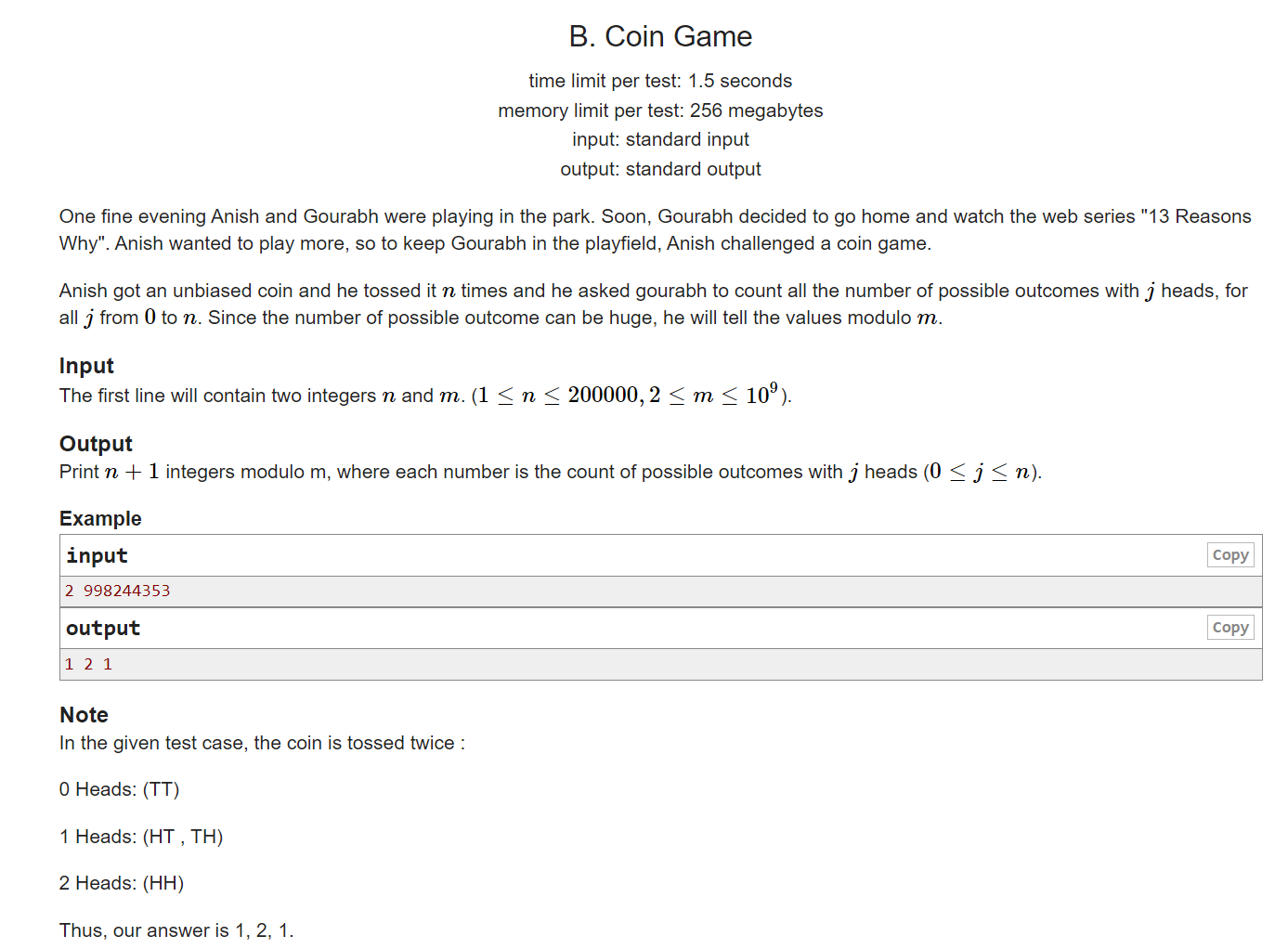
Anish got an unbiased coin and he tossed it n times and he asked Gourabh to count all the number of possible outcomes with j heads, for all j from 0 to n. Since the number of possible outcome can be huge, he will tell the values modulo m. To be clear, we need to return one integer per value of j.

The question is simple, but the problem arises with the time limit, being 1.5 seconds, but with input n as large as 200000.

I used math.comb to calculate the values, but it took more than 1.5 seconds to run.

So, are there any ways to calculate combinations in a faster way?

Edit#1:

Sample input: 2 998244353

Sample output: 1 2 1

Edit#2:

Here is the code that I've tried:

import math
 
n,m=input().split()
n = int(n)
m = int(m)
 
l = []
for i in range(n+1):
    l.append(math.comb(n,i)%m)
print(*l)

P.S: Please let me know if this is off topic for this site and suggest a suitable SE site to post this question. Thanks in advance! This question is from an inter college contest which ended 2 months ago.

Here is the original problem: https://codeforces.com/gym/430360/problem/B (you'll need an account, and first time follow the "Contest Link" here to enter).

In case you are not able to view the problem, please find the picture below.

Mccleary

Since it's modulo m, I strongly suspect that there is some math you can do here to convert it into an easy problem. If so, it is more a math problem than a programming problem. If you think I may be right, consider math.stackexchange.com . – Lermontov

@Lermontov I have posted it on Math.SE, but they suggested to post it here :) – Mccleary

Can you provide a complete set out inputs and the correct output? I'm not sure what is meant with the modulo m part. – Obtund

@ThibautB. I've added it now. – Mccleary

Added input and output to / of what? [SO]: How to create a Minimal, Reproducible Example (reprex (mcve)). – Hugues

@Barmar m is also an input. – Mccleary

The number of possible outcomes is 2**n. So what you're looking for is an efficient way of calculating sum(2**i % m for i in range(1, n+1)). – Bendy

@Bendy I guess we just need to print the values of nCr%m from r=0 to r=n, and not the sum of values. – Mccleary

Is there any constraint on m in the original question? If m is a prime number, then this is definitely a question about using Lucas' theorem. Note that 998244353 is, in fact, a prime number. – Valora

@Valora No, m can be any number from 2 to 10^9. – Mccleary

@Mccleary Does the problem description mean Gourabh has to count sequentially as Anish is flipping, reporting the number mod m after each flip? Or can he wait for Anish to flip 2000 times and then give him a cumulative answer mod some m? – Haploid

@Haploid I think no, but here is the complete question: codeforces.com/gym/430360/problem/B in case that helps. – Mccleary

Unfortunately the link requires an account to log in. I'm going to post a solution to the best of my understanding, and even if it's not quite what the original poser of the question had in mind perhaps it will nonetheless prove fruitful. – Haploid

It's probably enough to just compute the next value from the previous value instead of recomputing from scratch every time. – Colorific

I'm sorry, I don't know what to do. :( – Mccleary

Think about the mathematical relationship between n choose i and n choose i+1. – Colorific

@Colorific Dynamic Programming? – Mccleary

Not even dynamic programming, just a series. – Invagination

Also note that comb(n,k) == comb(n,n-k) – Invagination

@Colorific Depends on how you compute them. The naive way is still too slow. – Eiland

@KellyBundy: I'm not sure what you mean by that. By the "naive way", do you mean recomputing values from scratch? I tried writing up something to just compute n choose i+1 from n choose i, and came in well under the time limit, at least on the machine I was testing on. Didn't have to try any of the stuff I was thinking about for using modular multiplicative inverses to eliminate the division and perform the whole thing in modular arithmetic. – Colorific

@Colorific I meant computing the full bincoeffs and applying modulo m to each of them. Even just computing the bincoeffs (no modulo/print) took me ~16 seconds. – Eiland

@KellyBundy: Looks like my test was buggy - I used /= instead of //=. Yeah, modular arithmetic optimizations are necessary. – Colorific

@KellyBundy It wasn't an open contest iirc, please see this blog post: codeforces.com/blog/entry/114238 – Mccleary

@IvayloStrandjev Which of the answers to that other question can solve this here? That one is only about getting one value and the modulus is prime. Neither is the case here. (And it's a different language, which does play some role as well) – Eiland

@KellyBundy the idea is pretty similar, but indeed as m is not prime this changes things to an extent (I missed that bit yesterday). I don't think language is that big of a difference, typically problems on codeforces are designed in a way that with proper algorithm you can pass them with most popular languages. – Abydos

Answer 1

Using the usual multiplicative formula to compute the next number from the previous, but with keeping the numbers small. Let's first look at a naive version for clarity.

Naive

def naive(n, m):
    c = 1
    yield c
    for k in range(n):
        c = c * (n-k) // (k+1)
        yield c % m

n, m = map(int, input().split())
print(*naive(n, m))

Takes me ~30 seconds with n=200000. Because c grows very large, up to 60204 digits (199991 bits). And calculations with such large numbers are slow.

Fast

Instead of naively computing those large c and using modulo m only for output, let's keep c small throughout, modulo m. Got accepted on the site, taking ~0.68 seconds.

from math import gcd

def fast(n, m):
    c = 1
    G = 1
    yield c
    for k in range(n):

        mul = n - k
        while (g := gcd(mul, m)) > 1:
            mul //= g
            G *= g

        div = k + 1
        while (g := gcd(div, m)) > 1:
            div //= g
            G //= g

        c = c * mul * pow(div, -1, m) % m
        yield c * G % m

n, m = map(int, input().split())
print(*fast(n, m))

Attempt This Online!

Multiplication is fine under modulo. If it were only c = c * (n-k), we could just do c = c * (n-k) % m.

Division doesn't allow that. So instead of dividing by k+1, we multiply with its inverse (k+1)^-1 modulo m. The inverse of some number x is the number x^-1 so you get x·x^-1 = 1. For example, 7^-1 modulo 10 is 3. Because multiplying 7 and 3 gives you 21, which is 1 (modulo 10).

Next issue: Not all numbers have an inverse modulo m. For example, 6 doesn't have an inverse modulo 10. You can't multiply 6 with any integer and get 1 (modulo 10). Because 6 and 10 have common divisor 2. What we'll do is invert as much of 6 as possible. Extract the common divisor 2, leaving us with 3. That does have an inverse modulo 10 (namely 7).

So extract prime factors in the multipliers/divisors common with m into a separate number G. And update c with what remains, modulo m. Then combine c and G for output.

Rough times I get for n=200000, m=998244353 (the large prime from the question):

naive: 30.0 seconds
fast:   1.0 seconds
Matt's: 1.0 seconds

For n=200000, m=2*3*5*7*11*13*17*19*23:

naive: 30.0 seconds
fast:   1.2 seconds
Matt's: 4.8 seconds

I think worst case is a modulus with many primes like m=2*3*5*7*11*13*17*19*23, that maximizes my G. With n=200000, G grows up to 127 bits. Nothing to worry about.

My solution/explanation for a similar problem on Leetcode. That had modulus 10 and I hardcoded factors 2 and 5 and counted them instead of multiplying them into a number G like I did here. Maybe I'll revisit it with this general solution...

Progression

How do you know g divides G? – Weevil

@SimonGoater Similar to knowing that the // (k+1) in the naive version has no remainder. We only divide out what we multiply in. In the naive one it's more obvious, as we know the result is an integer. For the optimized one... We still only divide out what we multiplied in. Consider 7C3. That's (7*6*5) / (1*2*3), but we compute it as 1 * 7 / 1 * 6 / 2 * 5 / 3. At the point where we divide by 3, we have already multiplied by the 7, 6 and 5. Three consecutive numbers, one of them must have factor 3. So when we divide by 3, we just take out what we've already put in by multiplying with 6. – Progression

Answer 2

Since you need to output values for all j, you should use this generating function:

If j >= 1, then C(n,j) = C(n,j-1) * (n+1-j) / j

Normally, when this sort of question is asked, the modulus m is a prime larger than n. This makes it relatively easy to do all these calculations mod m, because every j will have a multiplicative inverse.

In fact, it is so unusual to ask this question with a non-prime modulus, that I bet the codeforces problem description just fails to mention it. I would try it with the prime modulus assumption.

If you're using python 3.8 or better, then there is a modular inverse built into the language, and you can do it just like this:

def getBinomialCoefficientsMod(n,m):
    result = [1]
    for j in range(1,n+1):
        result.append(( result[j-1] * (n+1-j) * pow(j,-1,m) )%m)
    return result

Edit: Well, it turns out that m is not always a large enough prime, and I don't want to leave this answer incomplete, so here's a version that works with composite or small m:

def getBinomialCoefficientsMod(n,m):

    # get the prime factors of the modulus
    facs=[]
    fac=2
    mleft = m
    while fac*fac<=mleft:
        if m%fac==0:
            facs.append(fac)
            while mleft%fac==0:
                mleft//=fac
        fac+=1
    if mleft>1:
        facs.append(mleft)

    result = [1]
    # factor of the last result that is relatively prime to m
    rpresult = 1
    # powers of the prime factors of m in the last result
    exponents = [0]*len(facs)

    for j in range(1,n+1):
        p=1
        num = n+1-j
        den = j

        # remove factors of the modulus from num and den,
        # track their exponents, and get their product
        for i in range(len(facs)):
            fac = facs[i]
            while num%fac==0:
                exponents[i]+=1
                num//=fac
            while den%fac==0:
                exponents[i]-=1
                den//=fac
            p = p*pow(fac,exponents[i],m)
    
        rpresult = (rpresult * num * pow(den,-1,m)) % m
    
        result.append(( rpresult * p )%m)

    return result

Dicotyledon

Perhaps the OP will try it and we shall see. Otherwise you can keep track of the exponents of factors of the modulus, but that's annoying :) – Dicotyledon

No, m need not be a prime number. The second test case has n=4 and m=6. – Mccleary

Oh well, I guess I'll make it work for composite m, then... – Dicotyledon

Did you try it at the site? Seems about 2-4 times slower than mine, which got accepted in ~0.7 seconds, so yours could be close. Our results match. – Progression

It could very well be slower, but that probably depends on the modulus. It took 0.6 seconds on my macbook for n,m = 200000,23454. I don't have a codeforces account. – Dicotyledon

Right, the modulus matters, at least for yours. With n=200000 and m=2*3*5*7*11*13*17*19*23, it's like me=1.2, you=4.8 seconds. I had tested that to maximize my G (equivalent to your p, I think). With the prime m=998244353, both take about 1 second. – Progression

Answer 3

I will sugest to use something like Modulo Multiplication.

If you have two numbers a and b, and you calculate their product modulo mod, you can take the modulo of each number first and then calculate the product. That is:

(a * b) % mod = ((a % mod) * (b % mod)) % mod

Taking into account that: C(n, r) = n! / (r! * (n - r)!) You can probably get some nice reduction of computation passing mod inside a getting a general result.

Fable

Yes, and to divide n! by (r! * (n - r)!) in modular arithmetics, you need to compute the modular multiplicative inverse of (r! * (n - r)!), and then % mod the answer. Since simple division does not work there. – Frumenty