How to make monotonic (increasing) smooth spline with smooth.spline() function?

Question

I have data that are strictly increasing and would like to fit a smoothing spline that is monotonically increasing as well with the smooth.spline() function if possible, due to the ease of use of this function.

For example, my data can be effectively reproduced with the example:

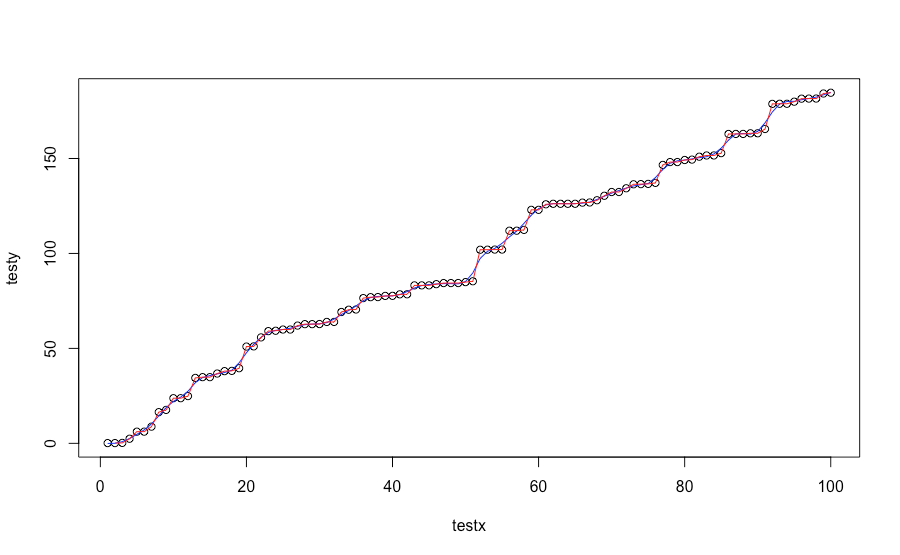
testx <- 1:100
testy <- abs(rnorm(length(testx)))^3
testy <- cumsum(testy)
plot(testx,testy)
sspl <- smooth.spline(testx,testy)
lines(sspl,col="blue")

which is not necessarily increasing everywhere. Any suggestions?

Kristianson

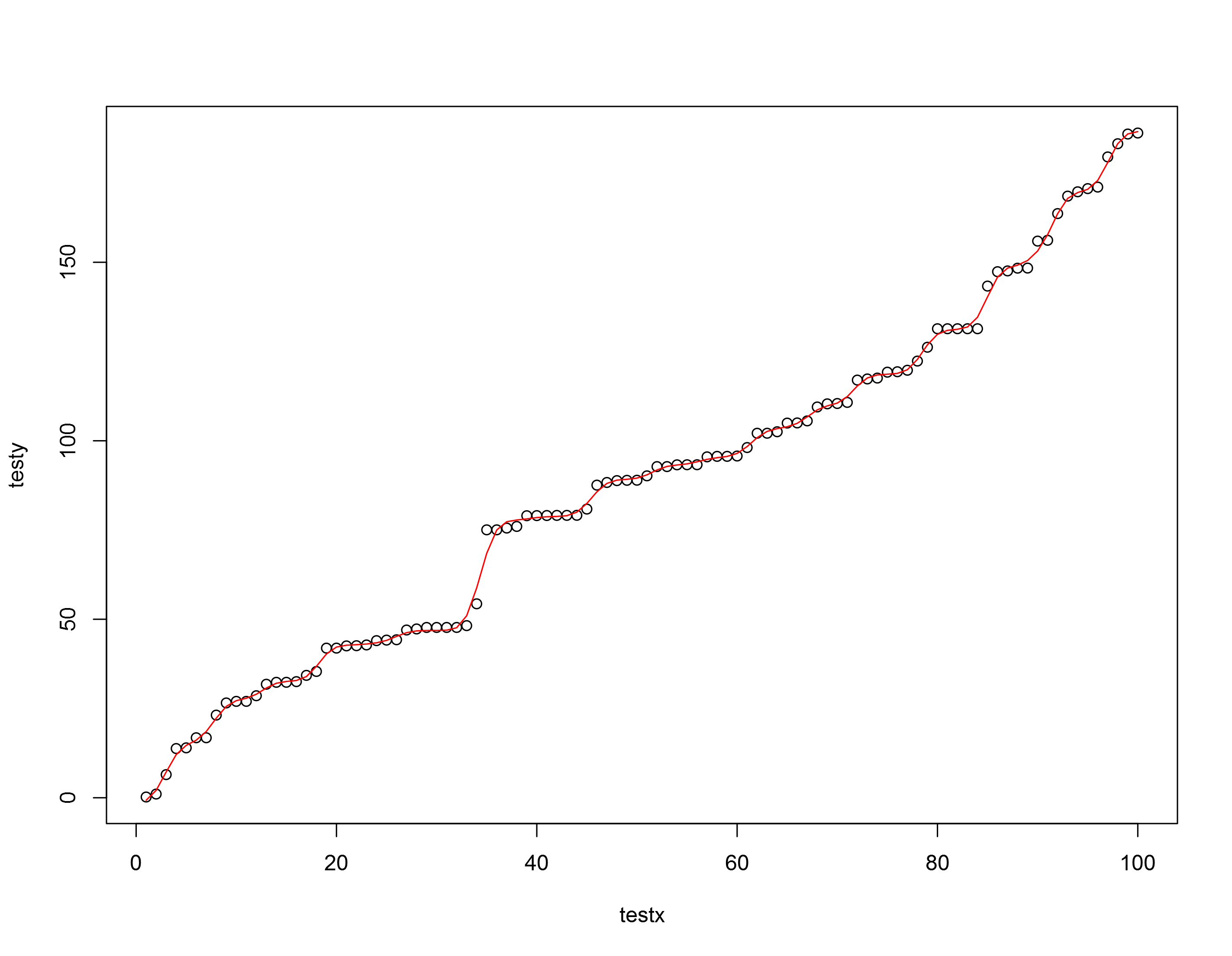
You can change some parameters to produce the behavior you want; this probably will have to be done on a case by case basis. sspl <- smooth.spline(testx,testy,tol = 3) (or binning) works for this particular dataset. – Saffron

Thanks! Unfortunately, I am looking for a generalizable solution. I.e. my data are always monotonic, but different every time I run the spline. – Kristianson

Given that the data is monotonically increasing, does a spline really make the most sense? Why not fit a monotonically increasing function? Just a thought. – Montemontefiascone

You could also check out lowess as an alternate fit method. The granularity can be adjusted with the f parameter. To generalize, you could wrap it in a method to try parameter options and check against min(diff(sspl$y,1)) to ensure monotonic behavior. – Montemontefiascone

Answer 1

This doesn't use smooth.spline() but the splinefun(..., method="hyman") will fit a monotonically increasing spline and is also easy to use. So for example:

testx <- 1:100
testy <- abs(rnorm(length(testx)))^3
testy <- cumsum(testy)
plot(testx,testy)
sspl <- smooth.spline(testx,testy)
lines(sspl,col="blue")
tmp <- splinefun(x=testx, y=cumsum(testy), method="hyman")
lines(testx[-1], diff(tmp(testx)), col="red")

Yields the following figure (red are the values from the monotonically increasing spline)

From the help file of splinefun: "Method "hyman" computes a monotone cubic spline using Hyman filtering of an method = "fmm" fit for strictly monotonic inputs. (Added in R 2.15.2.)"

Insensible

splinefun was exactly what I needed. To future readers: splinefun returns a new function that you can directly call, and does not return a fitted model in the traditional R sense. To predict new values using this fitted spline function, call that new created function and pass in your new data. This replaces the use of predict that you're used to from traditional model fits.E.g., MonotonicSpline <- splinefun(x = toFit$x, y = toFit$y, method = "hyman"); monotonicFit <- MonotonicSpline(inputVector) – Midway

This only works if all your original data are actually monotonically increasing, ie if there is no noise on your data (otherwise splinefun would return an error). If there is, then you can use shape-constrained splines in the scam or cobs packages, as mentioned below... – Gautier

In response to @TomWenseleers: you are correct about this working for only monotonically increasing data. This could arise from noisy data, however, where the underlying data are noisy but you have taken, say a cumulative sum, cumsum(). I have used this in the past to interpolate observations in a time-series with non-negative values. Where I want observations at a different timescale from my observed data. E.g. I want weekly data but I only have monthly observations on public health surveillance case counts (i.e. that must be greater than or equal to 0). – Insensible

Answer 2

You could use shape-constrained splines for this, e.g. using the scam package:

require(scam)
fit = scam(testy~s(testx, k=100, bs="mpi", m=5), 
            family=gaussian(link="identity"))
plot(testx,testy)
lines(testx,predict(fit),col="red")

Or if you would like to use L1 loss as opposed to L2 loss, which is less sensitive to outliers, you could also use the cobs package for this...

Advantage of this method compared to the solution above is that it also works if the original data perhaps are not 100% monotone due to the presence of noise...

Gautier

Great answer. For a single regressor, the cobs package is the most flexible of the two. – Dermatogen

Answer 3

I would suggest using loess for this type of monotonically increasing function.

Examining spline's derivative we see that it is negative and non-trivial in some cases:

> plot(testx,testy)
> sspl <- smooth.spline(testx,testy)
> min(diff(sspl$y))
[1] -0.4851321

If we use loess, I think this problem will be less severe.

 d <- data.frame(testx,testy)
 fit.lo <- loess(testy ~ testx,data=d)
 lines(fit.lo$x,fit.lo$y)

Then checking the derivative we get:

> min(diff(fit.lo$y))
[1] 1.151079e-12

Which is essentially 0. At near 0, we sometimes get a trivially small negative value.

Here is an example of the above loess fit.

Not sure if this will hold in all cases but it seems to do a better job than spline.

Montemontefiascone