Warning: timeit results may vary due to differences in hardware or
version of Python.
Below is a script which compares a number of implementations:
Many thanks to stephan for bringing sieve_wheel_30 to my attention.
Credit goes to Robert William Hanks for primesfrom2to, primesfrom3to, rwh_primes, rwh_primes1, and rwh_primes2.
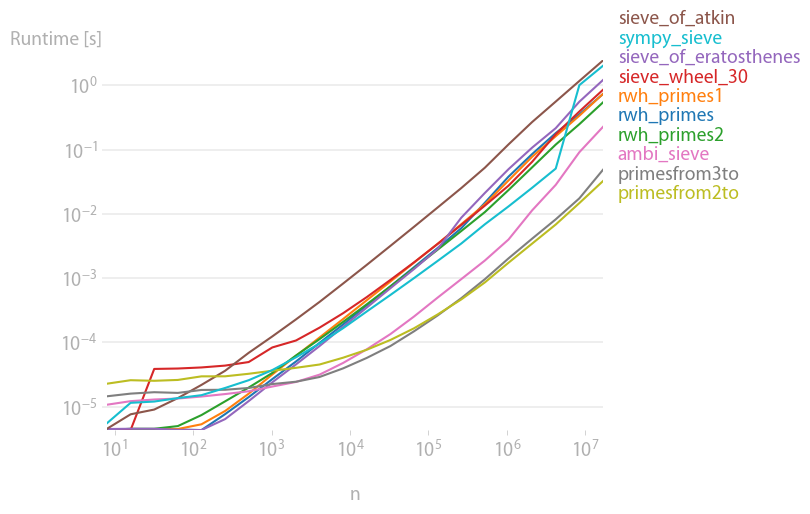
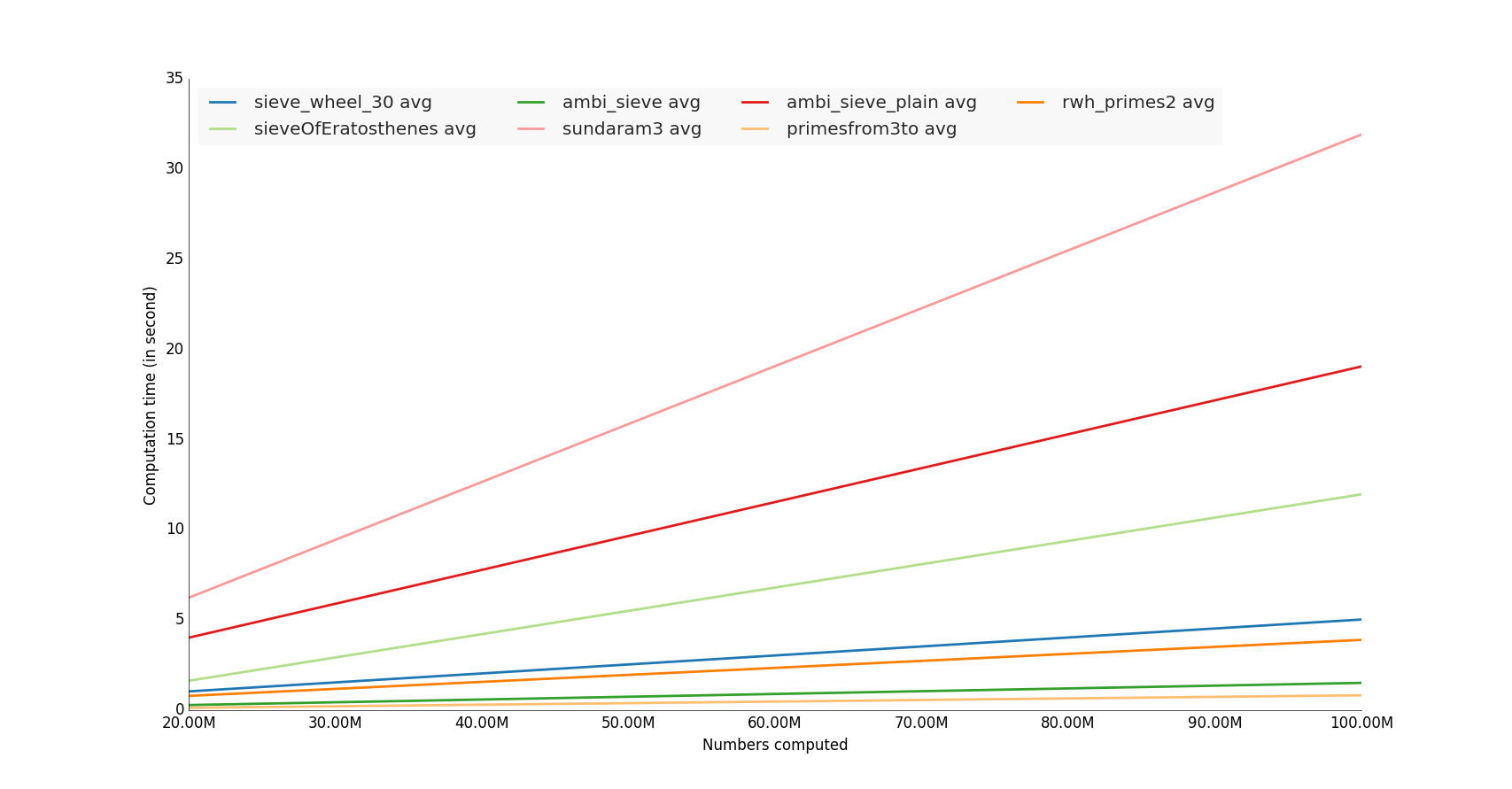
Of the plain Python methods tested, with psyco, for n=1000000,
rwh_primes1 was the fastest tested.
+---------------------+-------+
| Method | ms |
+---------------------+-------+
| rwh_primes1 | 43.0 |
| sieveOfAtkin | 46.4 |
| rwh_primes | 57.4 |
| sieve_wheel_30 | 63.0 |
| rwh_primes2 | 67.8 |
| sieveOfEratosthenes | 147.0 |
| ambi_sieve_plain | 152.0 |
| sundaram3 | 194.0 |
+---------------------+-------+
Of the plain Python methods tested, without psyco, for n=1000000,
rwh_primes2 was the fastest.
+---------------------+-------+
| Method | ms |
+---------------------+-------+
| rwh_primes2 | 68.1 |
| rwh_primes1 | 93.7 |
| rwh_primes | 94.6 |
| sieve_wheel_30 | 97.4 |
| sieveOfEratosthenes | 178.0 |
| ambi_sieve_plain | 286.0 |
| sieveOfAtkin | 314.0 |
| sundaram3 | 416.0 |
+---------------------+-------+
Of all the methods tested, allowing numpy, for n=1000000,
primesfrom2to was the fastest tested.
+---------------------+-------+
| Method | ms |
+---------------------+-------+
| primesfrom2to | 15.9 |
| primesfrom3to | 18.4 |
| ambi_sieve | 29.3 |
+---------------------+-------+
Timings were measured using the command:
python -mtimeit -s"import primes" "primes.{method}(1000000)"
with {method} replaced by each of the method names.
primes.py:
#!/usr/bin/env python
import psyco; psyco.full()
from math import sqrt, ceil
import numpy as np
def rwh_primes(n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/3035188#3035188
""" Returns a list of primes < n """
sieve = [True] * n
for i in xrange(3,int(n**0.5)+1,2):
if sieve[i]:
sieve[i*i::2*i]=[False]*((n-i*i-1)/(2*i)+1)
return [2] + [i for i in xrange(3,n,2) if sieve[i]]
def rwh_primes1(n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/3035188#3035188
""" Returns a list of primes < n """
sieve = [True] * (n/2)
for i in xrange(3,int(n**0.5)+1,2):
if sieve[i/2]:
sieve[i*i/2::i] = [False] * ((n-i*i-1)/(2*i)+1)
return [2] + [2*i+1 for i in xrange(1,n/2) if sieve[i]]
def rwh_primes2(n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/3035188#3035188
""" Input n>=6, Returns a list of primes, 2 <= p < n """
correction = (n%6>1)
n = {0:n,1:n-1,2:n+4,3:n+3,4:n+2,5:n+1}[n%6]
sieve = [True] * (n/3)
sieve[0] = False
for i in xrange(int(n**0.5)/3+1):
if sieve[i]:
k=3*i+1|1
sieve[ ((k*k)/3) ::2*k]=[False]*((n/6-(k*k)/6-1)/k+1)
sieve[(k*k+4*k-2*k*(i&1))/3::2*k]=[False]*((n/6-(k*k+4*k-2*k*(i&1))/6-1)/k+1)
return [2,3] + [3*i+1|1 for i in xrange(1,n/3-correction) if sieve[i]]
def sieve_wheel_30(N):
# http://zerovolt.com/?p=88
''' Returns a list of primes <= N using wheel criterion 2*3*5 = 30
Copyright 2009 by zerovolt.com
This code is free for non-commercial purposes, in which case you can just leave this comment as a credit for my work.
If you need this code for commercial purposes, please contact me by sending an email to: info [at] zerovolt [dot] com.'''
__smallp = ( 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139,
149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227,
229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311,
313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401,
409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491,
499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599,
601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683,
691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797,
809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887,
907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997)
wheel = (2, 3, 5)
const = 30
if N < 2:
return []
if N <= const:
pos = 0
while __smallp[pos] <= N:
pos += 1
return list(__smallp[:pos])
# make the offsets list
offsets = (7, 11, 13, 17, 19, 23, 29, 1)
# prepare the list
p = [2, 3, 5]
dim = 2 + N // const
tk1 = [True] * dim
tk7 = [True] * dim
tk11 = [True] * dim
tk13 = [True] * dim
tk17 = [True] * dim
tk19 = [True] * dim
tk23 = [True] * dim
tk29 = [True] * dim
tk1[0] = False
# help dictionary d
# d[a , b] = c ==> if I want to find the smallest useful multiple of (30*pos)+a
# on tkc, then I need the index given by the product of [(30*pos)+a][(30*pos)+b]
# in general. If b < a, I need [(30*pos)+a][(30*(pos+1))+b]
d = {}
for x in offsets:
for y in offsets:
res = (x*y) % const
if res in offsets:
d[(x, res)] = y
# another help dictionary: gives tkx calling tmptk[x]
tmptk = {1:tk1, 7:tk7, 11:tk11, 13:tk13, 17:tk17, 19:tk19, 23:tk23, 29:tk29}
pos, prime, lastadded, stop = 0, 0, 0, int(ceil(sqrt(N)))
# inner functions definition
def del_mult(tk, start, step):
for k in xrange(start, len(tk), step):
tk[k] = False
# end of inner functions definition
cpos = const * pos
while prime < stop:
# 30k + 7
if tk7[pos]:
prime = cpos + 7
p.append(prime)
lastadded = 7
for off in offsets:
tmp = d[(7, off)]
start = (pos + prime) if off == 7 else (prime * (const * (pos + 1 if tmp < 7 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 11
if tk11[pos]:
prime = cpos + 11
p.append(prime)
lastadded = 11
for off in offsets:
tmp = d[(11, off)]
start = (pos + prime) if off == 11 else (prime * (const * (pos + 1 if tmp < 11 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 13
if tk13[pos]:
prime = cpos + 13
p.append(prime)
lastadded = 13
for off in offsets:
tmp = d[(13, off)]
start = (pos + prime) if off == 13 else (prime * (const * (pos + 1 if tmp < 13 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 17
if tk17[pos]:
prime = cpos + 17
p.append(prime)
lastadded = 17
for off in offsets:
tmp = d[(17, off)]
start = (pos + prime) if off == 17 else (prime * (const * (pos + 1 if tmp < 17 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 19
if tk19[pos]:
prime = cpos + 19
p.append(prime)
lastadded = 19
for off in offsets:
tmp = d[(19, off)]
start = (pos + prime) if off == 19 else (prime * (const * (pos + 1 if tmp < 19 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 23
if tk23[pos]:
prime = cpos + 23
p.append(prime)
lastadded = 23
for off in offsets:
tmp = d[(23, off)]
start = (pos + prime) if off == 23 else (prime * (const * (pos + 1 if tmp < 23 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# 30k + 29
if tk29[pos]:
prime = cpos + 29
p.append(prime)
lastadded = 29
for off in offsets:
tmp = d[(29, off)]
start = (pos + prime) if off == 29 else (prime * (const * (pos + 1 if tmp < 29 else 0) + tmp) )//const
del_mult(tmptk[off], start, prime)
# now we go back to top tk1, so we need to increase pos by 1
pos += 1
cpos = const * pos
# 30k + 1
if tk1[pos]:
prime = cpos + 1
p.append(prime)
lastadded = 1
for off in offsets:
tmp = d[(1, off)]
start = (pos + prime) if off == 1 else (prime * (const * pos + tmp) )//const
del_mult(tmptk[off], start, prime)
# time to add remaining primes
# if lastadded == 1, remove last element and start adding them from tk1
# this way we don't need an "if" within the last while
if lastadded == 1:
p.pop()
# now complete for every other possible prime
while pos < len(tk1):
cpos = const * pos
if tk1[pos]: p.append(cpos + 1)
if tk7[pos]: p.append(cpos + 7)
if tk11[pos]: p.append(cpos + 11)
if tk13[pos]: p.append(cpos + 13)
if tk17[pos]: p.append(cpos + 17)
if tk19[pos]: p.append(cpos + 19)
if tk23[pos]: p.append(cpos + 23)
if tk29[pos]: p.append(cpos + 29)
pos += 1
# remove exceeding if present
pos = len(p) - 1
while p[pos] > N:
pos -= 1
if pos < len(p) - 1:
del p[pos+1:]
# return p list
return p
def sieveOfEratosthenes(n):
"""sieveOfEratosthenes(n): return the list of the primes < n."""
# Code from: <[email protected]>, Nov 30 2006
# http://groups.google.com/group/comp.lang.python/msg/f1f10ced88c68c2d
if n <= 2:
return []
sieve = range(3, n, 2)
top = len(sieve)
for si in sieve:
if si:
bottom = (si*si - 3) // 2
if bottom >= top:
break
sieve[bottom::si] = [0] * -((bottom - top) // si)
return [2] + [el for el in sieve if el]
def sieveOfAtkin(end):
"""sieveOfAtkin(end): return a list of all the prime numbers <end
using the Sieve of Atkin."""
# Code by Steve Krenzel, <[email protected]>, improved
# Code: https://web.archive.org/web/20080324064651/http://krenzel.info/?p=83
# Info: http://en.wikipedia.org/wiki/Sieve_of_Atkin
assert end > 0
lng = ((end-1) // 2)
sieve = [False] * (lng + 1)
x_max, x2, xd = int(sqrt((end-1)/4.0)), 0, 4
for xd in xrange(4, 8*x_max + 2, 8):
x2 += xd
y_max = int(sqrt(end-x2))
n, n_diff = x2 + y_max*y_max, (y_max << 1) - 1
if not (n & 1):
n -= n_diff
n_diff -= 2
for d in xrange((n_diff - 1) << 1, -1, -8):
m = n % 12
if m == 1 or m == 5:
m = n >> 1
sieve[m] = not sieve[m]
n -= d
x_max, x2, xd = int(sqrt((end-1) / 3.0)), 0, 3
for xd in xrange(3, 6 * x_max + 2, 6):
x2 += xd
y_max = int(sqrt(end-x2))
n, n_diff = x2 + y_max*y_max, (y_max << 1) - 1
if not(n & 1):
n -= n_diff
n_diff -= 2
for d in xrange((n_diff - 1) << 1, -1, -8):
if n % 12 == 7:
m = n >> 1
sieve[m] = not sieve[m]
n -= d
x_max, y_min, x2, xd = int((2 + sqrt(4-8*(1-end)))/4), -1, 0, 3
for x in xrange(1, x_max + 1):
x2 += xd
xd += 6
if x2 >= end: y_min = (((int(ceil(sqrt(x2 - end))) - 1) << 1) - 2) << 1
n, n_diff = ((x*x + x) << 1) - 1, (((x-1) << 1) - 2) << 1
for d in xrange(n_diff, y_min, -8):
if n % 12 == 11:
m = n >> 1
sieve[m] = not sieve[m]
n += d
primes = [2, 3]
if end <= 3:
return primes[:max(0,end-2)]
for n in xrange(5 >> 1, (int(sqrt(end))+1) >> 1):
if sieve[n]:
primes.append((n << 1) + 1)
aux = (n << 1) + 1
aux *= aux
for k in xrange(aux, end, 2 * aux):
sieve[k >> 1] = False
s = int(sqrt(end)) + 1
if s % 2 == 0:
s += 1
primes.extend([i for i in xrange(s, end, 2) if sieve[i >> 1]])
return primes
def ambi_sieve_plain(n):
s = range(3, n, 2)
for m in xrange(3, int(n**0.5)+1, 2):
if s[(m-3)/2]:
for t in xrange((m*m-3)/2,(n>>1)-1,m):
s[t]=0
return [2]+[t for t in s if t>0]
def sundaram3(max_n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/2073279#2073279
numbers = range(3, max_n+1, 2)
half = (max_n)//2
initial = 4
for step in xrange(3, max_n+1, 2):
for i in xrange(initial, half, step):
numbers[i-1] = 0
initial += 2*(step+1)
if initial > half:
return [2] + filter(None, numbers)
################################################################################
# Using Numpy:
def ambi_sieve(n):
# http://tommih.blogspot.com/2009/04/fast-prime-number-generator.html
s = np.arange(3, n, 2)
for m in xrange(3, int(n ** 0.5)+1, 2):
if s[(m-3)/2]:
s[(m*m-3)/2::m]=0
return np.r_[2, s[s>0]]
def primesfrom3to(n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/3035188#3035188
""" Returns a array of primes, p < n """
assert n>=2
sieve = np.ones(n/2, dtype=np.bool)
for i in xrange(3,int(n**0.5)+1,2):
if sieve[i/2]:
sieve[i*i/2::i] = False
return np.r_[2, 2*np.nonzero(sieve)[0][1::]+1]
def primesfrom2to(n):
# https://mcmap.net/q/86560/-fastest-way-to-list-all-primes-below-n/3035188#3035188
""" Input n>=6, Returns a array of primes, 2 <= p < n """
sieve = np.ones(n/3 + (n%6==2), dtype=np.bool)
sieve[0] = False
for i in xrange(int(n**0.5)/3+1):
if sieve[i]:
k=3*i+1|1
sieve[ ((k*k)/3) ::2*k] = False
sieve[(k*k+4*k-2*k*(i&1))/3::2*k] = False
return np.r_[2,3,((3*np.nonzero(sieve)[0]+1)|1)]
if __name__=='__main__':
import itertools
import sys
def test(f1,f2,num):
print('Testing {f1} and {f2} return same results'.format(
f1=f1.func_name,
f2=f2.func_name))
if not all([a==b for a,b in itertools.izip_longest(f1(num),f2(num))]):
sys.exit("Error: %s(%s) != %s(%s)"%(f1.func_name,num,f2.func_name,num))
n=1000000
test(sieveOfAtkin,sieveOfEratosthenes,n)
test(sieveOfAtkin,ambi_sieve,n)
test(sieveOfAtkin,ambi_sieve_plain,n)
test(sieveOfAtkin,sundaram3,n)
test(sieveOfAtkin,sieve_wheel_30,n)
test(sieveOfAtkin,primesfrom3to,n)
test(sieveOfAtkin,primesfrom2to,n)
test(sieveOfAtkin,rwh_primes,n)
test(sieveOfAtkin,rwh_primes1,n)
test(sieveOfAtkin,rwh_primes2,n)
Running the script tests that all implementations give the same result.

import antigravity. Isn't there anything likerequire 'prime'; Prime.take(10)(Ruby)? – Ahmadahmardifference_update. You can simply donumbers.difference_update(xrange(p*2, N+1, p))That will shave a few milliseconds off your time at the very least. – Jackpotfrom sympy import sieve; sieve.extend(N);– Amaryn =10000asnumber.pop()doesn't pop out the least one as not sorted. Thread – Bipetalous