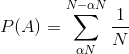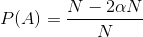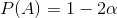Probabilty based on quicksort partition

Question

I have come across this question:

Let 0<α<.5 be some constant (independent of the input array length n). Recall the Partition subroutine employed by the QuickSort algorithm, as explained in lecture. What is the probability that, with a randomly chosen pivot element, the Partition subroutine produces a split in which the size of the smaller of the two subarrays is ≥α times the size of the original array?

Its answer is 1-2*α.

Can anyone explain me how has this answer come?Please Help.

Alcides

This might do better over at CS.SE considering it's of a more theoretical nature – Myasthenia

@Quirliom : thanks. I have posted this question on cs.stackexchange. – Alcides

You should mention that this question is from this Coursera course, week 3, and that it is against their honor code to publicly seek answers. In other words, when you're asking for solutions to homework problems, be upfront about it. – Limes

Answer 1

The choice of the pivot element is random, with uniform distribution.

There are N elements in the array, and we will assume that N is large (or we won't get the answer we want).

If 0≤α≤1, the probability that the number of elements smaller than the pivot is less than αN is α. The probability that the number of elements greater than the pivot is less than αN is the same. If α≤ 1/2, then these two possibilities are exclusive.

To say that the smaller subarray is of length ≥αN, is to say that neither of these conditions holds, therefore the probability is 1-2α.

Aixenprovence

Answer 2

The other answers didn't quite click with me so here's another take:

If at least one of the 2 subarrays must be you can deduce that the pivot must also be in position . This is obvious by contradiction. If the pivot is then there is a subarray smaller than . By the same reasoning the pivot must also be . Any larger value for the pivot will yield a smaller subarray than on the "right hand side".

This means that , as shown by the diagram below:

What we want to calculate then is the probability of that event (call it A) i.e .

The way we calculate the probability of an event is to sum of the probability of the constituent outcomes i.e. that the pivot lands at .

That sum is expressed as:

Which easily simplifies to:

With some cancellation we get:

Crosson

i believe 1-2*alpha does not work for example , array = { 1,2,3,4,5} alpha = 0.3 **************** According to the formula , Probability = 1-2*0.3 = 0.4 **************** However, there is only 1 pivot (3) , which could partition into 2 arrays each of size 2 , hence smallest is 2 >= 0.3*5 = 1.5, rest of all pivots will have smaller sub array to be of size 1 and is not >= 1.5 **************** Hence , the probability is 1 (only one pivot 3) / 5 (all possible pivots) = 0.2, which is negating 0.4 – Henleyonthames

Thank you! I'm not the OP, but this answer really made sense to me unlike some of the others – Palaestra

Wow! Thank you, that's the best answer I've read about that exercise. – Azygous

Answer 3

Just one more approach for solving the problem (for those who have uneasy time understanding it, like I have).

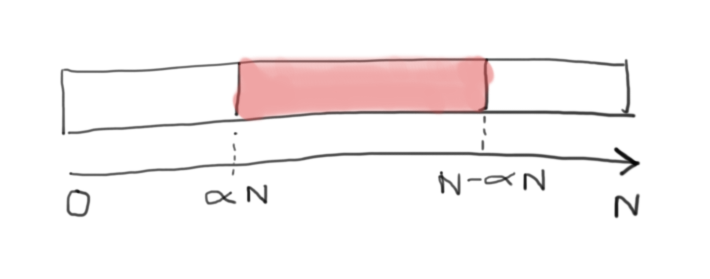
First. Since we are talking about "the smaller of the two subarrays", then its length is less than 1/2 * n (n - the number of elements in original array).

Second. If 0 < a < 0.5 it means the a * n is less than 1/2 * n either. And thus we are talking from now about two randomly chosen integers bounded by 0 at lowest and 1/2 * n at highest.

Third. Lets imagine the dice with numbers from 1 to 6 on it's sides. Lets choose a number from 1 to 6, for example 4. Now roll the dice. Each number has a probability 1/6 to be the outcome of this roll. Thus for event "outcome is less or equal to 4" we have probability equal to the sum of probabilities of each of this outcomes. And we have numbers 1, 2, 3 and 4. Altogether p(x <= 4) = 4 * 1/6 = 4/6 = 2/3. So the probability of event "output is bigger than 4" is p(x > 4) = 1 - p(x <= 4) = 1 - 2/3 = 1/3.

Fourth. Lets go back to our problem. The "chosen number" is now a * n. And we are going to roll the dice with the numbers from 0 to (1/2 * n) on it to get k - the number of elements in a smallest of subarrays. The probability that outcome is bounded by (a * n) at highest is equals to sum of the probabilities of all outcomes from 0 to (a * n). And the probability for any particular outcome k is p(k) = 1 / (1/2 * n).

Therefore p(k <= a * n) = (a * n) * (1 / (1/2 * n)) = 2 * a.

From this we can easily conclude that p(k > a * n) = 1 - p(k <= a * n) = 1 - 2 * a.

Stillas

Answer 4

Array length is n. For smaller array length >= αn pivot should be greater than αn number of elements. At the same time pivot should be smaller than αn number of elements( else smaller array size will be less than required)

So out of n element we have to select one among (n-2α)n elements.

required probability is n(1-2α)/n.

Hence 1-2α

Trice

What do you mean by "pivot should be greater than αn number of elements. At the same time pivot should be smaller than αn number of elements"? Those two seem to be contradicting each other. – Tomfool

Answer 5

The probability would be, the number of desired elements/Total number of elements. In this case, ((1-αn)-(αn))/n Since α lies between,0 and 0.5,(1-α) must be bigger than α.Hence the number of elements contained between them would be, (1-α-α)n=(1-2α)n and so,the probability would be, (1-2α)n/n=1-2α

Coumarin

Answer 6

Another approach: List the "more balanced" options:

αn + 1 to (1 - α)n - 1

αn + 2 to (1 - α)n - 2

...

αn + k to (1 - α)n - k

So k in total. We know that the most balanced is n / 2 to n / 2, so:

 αn + k = n / 2 => k = n(1/2 - α)

Similarly, list the "less balanced" options:

αn - 1 to (1 - α)n + 1

αn - 2 to (1 - α)n + 2

...

αn - m to (1 - α)n + m

So m in total. We know that the least balanced is 0 to n so:

αn - m = 0 => m = αn

Since all these options happen with equal probability we can use the frequency definition of probability so:

Pr{More balanced} = (total # of more balanced) / (total # of options) =>

Pr{More balanced} = k / (k + m) = n(1/2 - α) / (n(1/2 - α) + αn) = 1 - 2α

Foushee