Calculating Area of Irregular Polygon in C#

Question

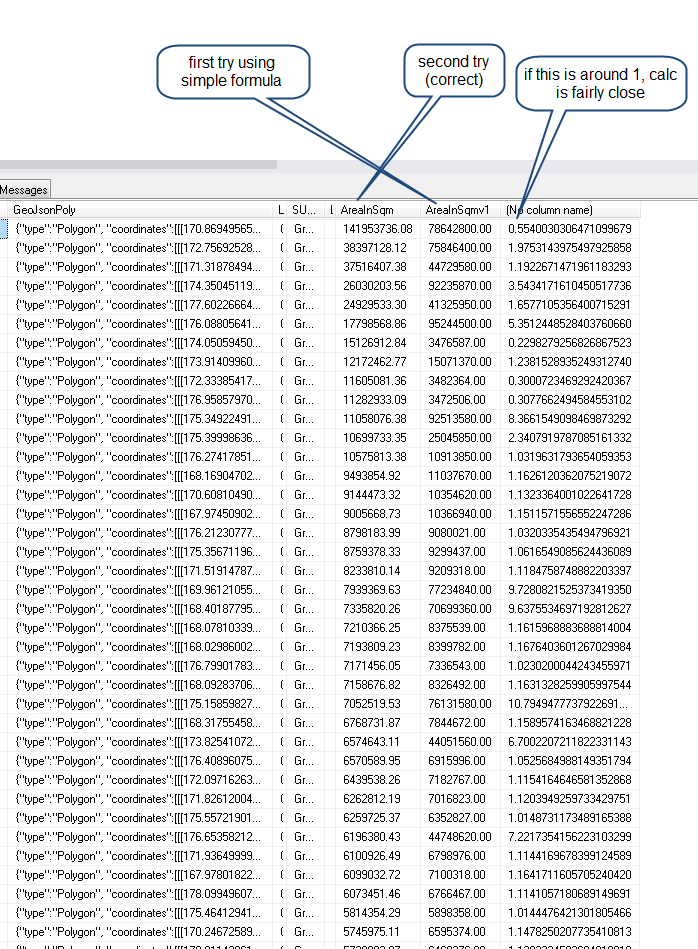
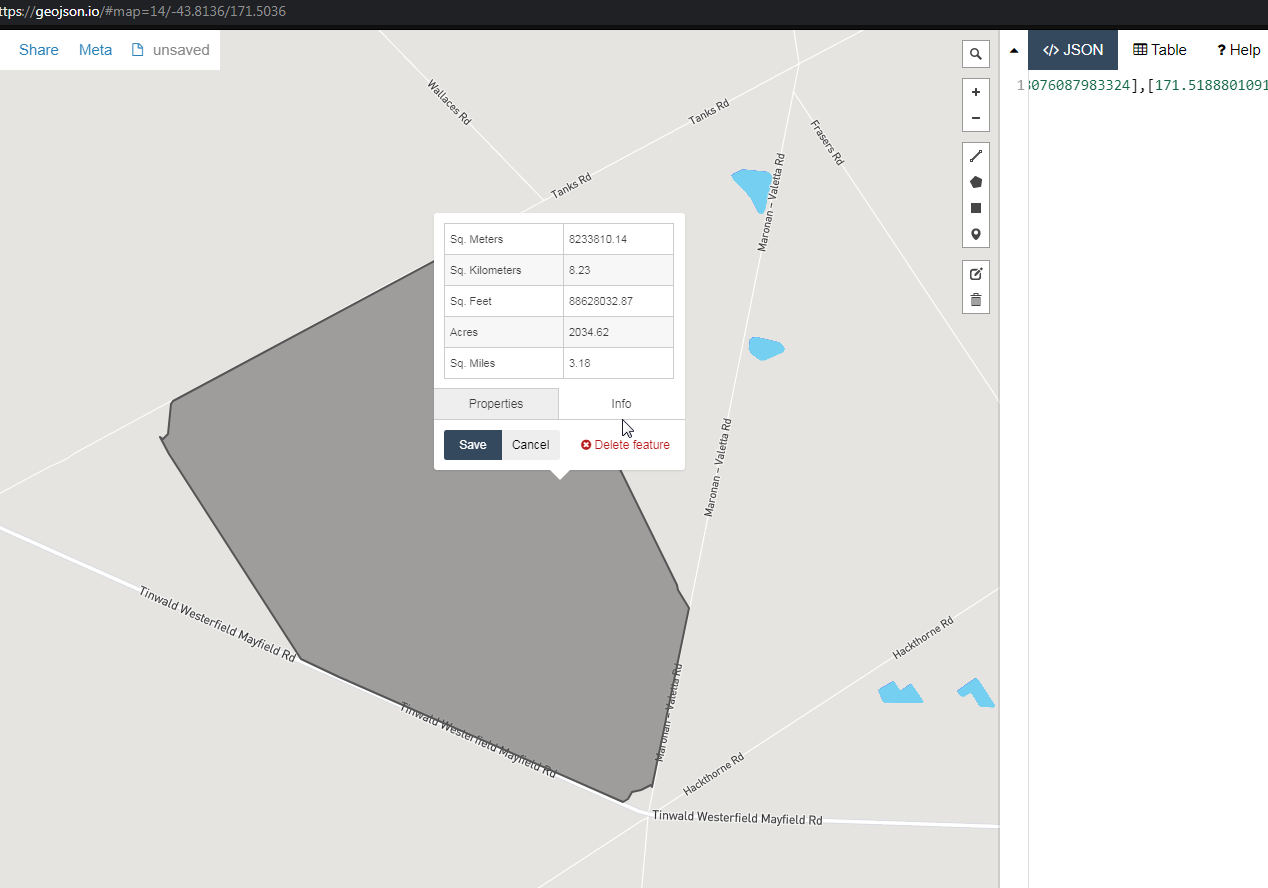
I've managed to write a 'for dummies' how to calculate the area of irregular polygon in C#, but I need it to be dynamic for any amount of verticies.

Can someone please help?

Class:

public class Vertex
{
    private int _vertexIdx;
    private double _coordX;
    private double _coordY;
    private double _coordZ;

    public Vertex()
    { }

    public Vertex(int vertexIdx, double coordX, double coordY, double coordZ)
    {
        _vertexIdx = vertexIdx;
        _coordX = coordX;
        _coordY = coordY;
        _coordZ = coordZ;
    }

    public int VertexIdx
    {
        get { return _vertexIdx; }
        set { _vertexIdx = value; }
    }

    public double X
    {
        get { return _coordX; }
        set { _coordX = value; }
    }

    public double Y
    {
        get { return _coordY; }
        set { _coordY = value; }
    }

    public double Z
    {
        get { return _coordZ; }
        set { _coordZ = value; }
    }
}

Form_Load:

List<Vertex> verticies = new List<Vertex>();

verticies.Add(new Vertex(1, 930.9729, 802.8789, 0));
verticies.Add(new Vertex(2, 941.5341, 805.662, 0));
verticies.Add(new Vertex(3, 946.5828, 799.271, 0));
verticies.Add(new Vertex(4, 932.6215, 797.0548, 0));

dataGridView1.DataSource = verticies;

Code to calculate when button is pressed: (hard-coded for 4 points polygon - should be for any amount...)

        // X-coords
        double x1;
        double x2;
        double x3;
        double x4;
        double x5;

        // Y-coords
        double y1;
        double y2;
        double y3;
        double y4;
        double y5;

        // Xn * Yn++
        double x1y2;
        double x2y3;
        double x3y4;
        double x4y5;

        // Yn * Xn++
        double y1x2;
        double y2x3;
        double y3x4;
        double y4x5;

        // XnYn++ - YnXn++
        double x1y2my1x2;
        double x2y3my2x3;
        double x3y4my3x4;
        double x4y5my4x5;

        double result;
        double area;

        x1 = Convert.ToDouble(dataGridView1.Rows[0].Cells[1].Value.ToString());
        y1 = Convert.ToDouble(dataGridView1.Rows[0].Cells[2].Value.ToString());
        txtLog.Text += String.Format("X1 = {0}\tY1 = {1}\r\n", x1, y1);

        x2 = Convert.ToDouble(dataGridView1.Rows[1].Cells[1].Value.ToString());
        y2 = Convert.ToDouble(dataGridView1.Rows[1].Cells[2].Value.ToString());
        txtLog.Text += String.Format("X2 = {0}\tY2 = {1}\r\n", x2, y2);

        x3 = Convert.ToDouble(dataGridView1.Rows[2].Cells[1].Value.ToString());
        y3 = Convert.ToDouble(dataGridView1.Rows[2].Cells[2].Value.ToString());
        txtLog.Text += String.Format("X3 = {0}\tY3 = {1}\r\n", x3, y3);

        x4 = Convert.ToDouble(dataGridView1.Rows[3].Cells[1].Value.ToString());
        y4 = Convert.ToDouble(dataGridView1.Rows[3].Cells[2].Value.ToString());
        txtLog.Text += String.Format("X4 = {0}\tY4 = {1}\r\n", x4, y4);

        // add the start point again
        x5 = Convert.ToDouble(dataGridView1.Rows[0].Cells[1].Value.ToString());
        y5 = Convert.ToDouble(dataGridView1.Rows[0].Cells[2].Value.ToString());
        txtLog.Text += String.Format("X5 = {0}\tY5 = {1}\r\n", x5, y5);
        txtLog.Text += "\r\n";

        // Multiply 
        x1y2 = x1 * y2;
        x2y3 = x2 * y3;
        x3y4 = x3 * y4;
        x4y5 = x4 * y5;

        y1x2 = y1 * x2;
        y2x3 = y2 * x3;
        y3x4 = y3 * x4;
        y4x5 = y4 * x5;

        // Subtract from each other
        x1y2my1x2 = x1y2 - y1x2;
        x2y3my2x3 = x2y3 - y2x3; 
        x3y4my3x4 = x3y4 - y3x4;
        x4y5my4x5 = x4y5 - y4x5;

        // Sum all results
        result = x1y2my1x2 + x2y3my2x3 + x3y4my3x4 + x4y5my4x5;
        area = Math.Abs(result / 2);

        txtLog.Text += String.Format("Area = {0}\r\n", area);

Example output:

X1 = 930.9729 Y1 = 802.8789

X2 = 941.5341 Y2 = 805.662

X3 = 946.5828 Y3 = 799.271

X4 = 932.6215 Y4 = 797.0548

X5 = 930.9729 Y5 = 802.8789

Area = 83.2566504099523

Phillisphilly

A typical method that I've seen before is to partition the polygon into triangles, then you could simply sum the area of all the triangles. This is nontrivial however as it needs different algorithms depending on the complexity of the polygons (crossing edges, holes, convex/concave, etc.) – Houphouetboigny

You might consider asking this question on mathoverflow.net, a Stack Overflow-like site, only for math questions, just make sure you pose the question as a non-programming one and instead ask for the algorithmic approach. – Houphouetboigny

MathOverflow is for professional mathematicians who want to talk about problems in post-graduate-level mathematics. – Sw

Ok, no wonder it all sounded like a foreign language to me :) – Houphouetboigny

Answer 1

Using lambda expressions this becomes trivial!

var points = GetSomePoints();

points.Add(points[0]);
var area = Math.Abs(points.Take(points.Count - 1)
   .Select((p, i) => (points[i + 1].X - p.X) * (points[i + 1].Y + p.Y))
   .Sum() / 2);

The algorithm is explained here:

[This method adds] the areas of the trapezoids defined by the polygon's edges dropped to the X-axis. When the program considers a bottom edge of a polygon, the calculation gives a negative area so the space between the polygon and the axis is subtracted, leaving the polygon's area.

The total calculated area is negative if the polygon is oriented clockwise [so the] function simply returns the absolute value.

This method gives strange results for non-simple polygons (where edges cross).

Berner

The linked "explanation" does not explain the algorithm. It just presents the code differently. – Clorindaclorinde

Though I appreciate the succinctness, I must partially agree with @cp.engr; probably not the most maintainable (readable) solution. If I end up doing something like this, hopefully I'll post a simpler-to-understand alternative – Maraca

IMPORTANT, the polygon you define MUST be closed for this to work, i.e. the first point must be repeated at the end. See LinqPad Gist for example: gist.github.com/elliz/9d7da1fa74a76d84be4600dcbc121bd6 – Somatology

Whats if the closed polygon has several overlaps? Will this method correct for the case?> – Prato

You mean a self-intersecting polygon? It will give wrong results, as mentioned in the answer. Not sure how you would even define an area for such a polygon. – Berner

Answer 2

Something like that for a plane polygon (compiled with notepad):

static double GetDeterminant(double x1, double y1, double x2, double y2)
{
    return x1 * y2 - x2 * y1;
}

static double GetArea(IList<Vertex> vertices)
{
    if(vertices.Count < 3)
    {
        return 0;
    }
    double area = GetDeterminant(vertices[vertices.Count - 1].X, vertices[vertices.Count - 1].Y, vertices[0].X, vertices[0].Y);
    for (int i = 1; i < vertices.Count; i++)
    {
        area += GetDeterminant(vertices[i - 1].X, vertices[i - 1].Y, vertices[i].X, vertices[i].Y);
    }
    return area / 2;
}

Although your approach doesn't pay attention to Z-axis. Therefore I'd advice to apply some transformation to get rid of it: you won't be able to get area if the polygon is not plane, whereas if it is plane you are able to get rid of the third dimension.

Jibber

so, there is a diffrence between the area calculated in 2D and 3D? – Phillisphilly

Yes, just a little bit. Area can be calculated for plain objects ONLY. Therefore your polygon MUST be plain - all its vertices should lie in the same plain, otherwise area cannot be calculated. The problem is that this plane won't always be Z=0 plane as in your example. You should take this into consideration and process the points appropriately before calculating the area. – Jibber

Answer 3

public float Area(List<PointF> vertices)
{
    vertices.Add(vertices[0]);
    return Math.Abs(vertices.Take(vertices.Count - 1).Select((p, i) => (p.X * vertices[i + 1].Y) - (p.Y * vertices[i + 1].X)).Sum() / 2);
}

Eisegesis

Please provide some explanation to make your answer easiert to be understood. – Barny

Answer 4

I've found that when calculating the area for approx 600,000 polygons, the basic formulae shown above worked for some polygons, but a lot were out by a huge degree. I was spot checking my results against https://geojson.io/ - which returned correct results for very complex polygons with holes in them (e.g. lakes in the middle). In order to calculate the correct area for a complex polygon, I ended up using the same system that geojson.io uses - a client side js library Turf.js see here https://turfjs.org/docs/#area

In this image, you can see my first try, then my second using Turf.js - there is a column there showing a ratio of how correct the first try was compared to the second where 1 is the same calculation. You can see that they are mostly close, but some are out by a factor of 10 or worse.

Here is some sample code to do the calculation. I had it load 200 onto the screen, then run the calculation in JS, and ajax the result back to the server side database.

            $(document).ready(function () {
            var items = $('.geojson');
            for (var sc = 0; sc < items.length; sc++) {
                var id = $(items[sc]).attr('data-id');
                var polyData = JSON.parse($(items[sc]).find('.geojson-data').html());
                //console.log('[' + polyData + ']');
                var polygon = turf.polygon(polyData.coordinates);

                var area = turf.area(polygon);
                console.log('id[' + id + ']sqm[' + area + ']');

                    
                $(items[sc]).closest('tr').find('.data-id').html(id);
                var answerDom = $(items[sc]).closest('tr').find('.answer');

                if (true) {
                    $.ajax({
                        url: 'calc-poly-area-from-geojson-turf-scheduled.aspx',
                        type: "get",
                        data: {id:id, area: area },
                        invokedata: { answerDom: answerDom, area: area },
                        async: true,//run all at the same time
                        cache: false,
                        success: function (data) {
                            //console.log('test email done');

                            $(this.invokedata.answerDom).html('ok:' + this.invokedata.area);
                            $(this.invokedata.answerDom).removeClass('answer');

                            if ($('.answer').length == 0) {
                                window.location.reload();
                            }
                        },
                        error: function (msg) {
                            console.log("call failed: " + msg.responseText);
                            $(el).html('error in call');

                            //prompt('copy this',url+'?'+qs)
                        }
                    });
                }
            }
        });

        window.setTimeout(function () { window.location.reload(); }, 10000);

where an example polygon is here

{"type":"Polygon", "coordinates":[[[171.519147876006,-43.809111826162],[171.519264282931,-43.8094307100015],[171.519615782201,-43.8097268361192],[171.519874096036,-43.8097860548424],[171.525264107563,-43.8176887926426],[171.525356625489,-43.8179845471556],[171.525750029905,-43.8185636705947],[171.526002901974,-43.8187934292356],[171.526154917292,-43.8189686576417],[171.526249645477,-43.8191111884506],[171.526245660987,-43.819269203656],[171.526032299227,-43.8200263808647],[171.524134038501,-43.8268225827224],[171.523301803308,-43.8297987275054],[171.523129147529,-43.8301621243769],[171.522991616155,-43.8300725313285],[171.52248605771,-43.8302181414427],[171.522128893843,-43.8304084928376],[171.521558488905,-43.8304389785399],[171.521371202269,-43.830481916342],[171.521023295734,-43.8309120441211],[171.520774217465,-43.8310054055632],[171.520589483523,-43.8311387384524],[171.515210823266,-43.8294163992962],[171.514763136723,-43.8292736695248],[171.496256757791,-43.8233680542711],[171.494338310605,-43.8227558913632],[171.493450128779,-43.8224739752289],[171.493221517911,-43.8223838125259],[171.493001278557,-43.8222877021167],[171.492654147639,-43.821801588707],[171.491048512765,-43.8200169686591],[171.488157604579,-43.8168246695455],[171.488051808197,-43.8166695752984],[171.487648717141,-43.8162207994268],[171.486147094889,-43.8145461538075],[171.482241975825,-43.8101769774879],[171.481683765874,-43.8095751045999],[171.480858016595,-43.8085443728491],[171.481124633337,-43.8086557677844],[171.481334008334,-43.8085534985925],[171.481540735171,-43.8083379086683],[171.4815994175,-43.8077828104991],[171.481763314624,-43.8074471226617],[171.481812168914,-43.8064706917151],[171.48196041271,-43.8063093336607],[171.482260412185,-43.8062322290662],[171.482916004007,-43.8059780008537],[171.494844864468,-43.8013540958407],[171.501308718774,-43.7988446798756],[171.506019390319,-43.797017657826],[171.508275460952,-43.7961421972998],[171.508430707528,-43.7960805551645],[171.509117292333,-43.7963432108869],[171.510511038963,-43.7968679021071],[171.513299102675,-43.8007637699317],[171.513465917258,-43.8010892007185],[171.513696634335,-43.8013818859084],[171.513929550742,-43.8016136793445],[171.514114411714,-43.8018826827151],[171.514305634465,-43.8021912982997],[171.51440028511,-43.8024789426394],[171.514828618996,-43.8028429251794],[171.51494106207,-43.8031623582355],[171.515852739466,-43.8044825303059],[171.516111930457,-43.8047763591375],[171.517116748697,-43.8062534995253],[171.517374596163,-43.8065473602078],[171.517549793874,-43.8068229401963],[171.5176213721,-43.8070824951625],[171.517796573697,-43.8073580748019],[171.518070610117,-43.8076087983324],[171.518880109148,-43.8088563353488],[171.519147876006,-43.809111826162]]]}

you can paste that into geojson.io to check their area (click on poly, then 'properties' tab)

Flavor

Thats becasue Turf.js gives you the area exposes on a sphere not on a plane. as shown here – Heehaw