By definition, the Euler Totient function φ(.) is given by
![enter image description here]()
The python implementation to compute φ(.) is pretty straightforward:
def Euler_totient_def(n): # φ(n)
return sum([gcd(i, n) == 1 for i in range(1, n)]
def gcd(a, b): # complexity O(lg a)
while b:
a, b = b, a % b
return a
Also, by the fundamental theorem of arithmetic and by the property of the Totient function φ(.), we have,
![enter image description here]()
and the corresponding implementation:
def sieve_Eratosthenes(n): # precompute primes <= n: complexity O(n lglg n)
P = np.ones(n+1, dtype=int)
P[0:2] = 0
for e in range(2, n+1):
P[range(2*e, n+1, e)] = 0
return [i for i in range(n+1) if P[i]]
def factorize(n, P=None): # prime factorization of n with precomputed table P: complexity O(lg n)
if P is None:
P = sieve_Eratosthenes(n)
i = 0
f = set([])
while n > 1:
if n % P[i] == 0:
n //= P[i]
f.add(P[i])
else:
i += 1
return f
def Euler_totient_prime_factors(n, P): # φ(n)
f = factorize(n, P)
return int(n*np.prod([(1-1/p) for p in f]))
Now let's compare the time to compute φ(.) with both the above implementations:
import numpy as np
from time import time
n = 1234571
start = time()
print(Euler_totient_prime_factors(n, sieve_Eratosthenes(n)))
# 1089792
# prime factorization of n: 13 x 23 x 4129
print(time() - start)
# 23.920003175735474
start = time()
print(Euler_totient_def(n))
# 1089792
print(time() - start)
# 5.4549994468688965
The first implementation is much faster, as can be seen above. The precomputed prime table comes handy when we want to compute φ(.) for a bulk of numbers instead of a single number, as shown below:
def Euler_totients_prime_factors(a, N): # compute φ for numbers in list a
P = sieve_Eratosthenes(N)
return [Euler_totient_prime_factors(n, P) for n in a]
def Euler_totients_def(a): # compute φ for numbers in list a
return [Euler_totient_def(n) for n in a]
Now let's compute φ(.) for a list of numbers:
a = [12345, 123456, 1234561, 1234563, 1234567, 1234569, 1234571]
start = time()
print(Euler_totients_prime_factors(a, max(a)))
# [6576, 41088, 1228500, 704880, 1224720, 705456, 1089792]
# prime factorization 12345 = 3 x 5 x 823
# 123456 = 2^6 x 3 x 643
# 1234561 = 211 x 5851
# 1234563 = 3 x 11^2 x 19 x 179
# 1234567 = 127 x 9721
# 1234569 = 3 x 7 x 58789
# 1234571 = 13 x 23 x 4129
print(time() - start)
# 13.774996757507324
Ac can be seen from above, now the prime factorization with precomputed prime table computes φ values faster
start = time()
print(Euler_totients_def(a))
# [6576, 41088, 1228500, 704880, 1224720, 705456, 1089792]
print(time() - start)
# 18.693108558654785

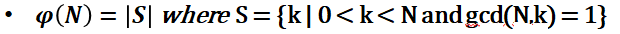

1/idoes not do what you think it does - try it. – Ginniferfrom __future__ import divisionat the top of your code to enable float division in Python 2. – Fastidious