Using sequence:
f <- function(v, x){
d = diff(c(0, which(v == x)))
vec <- sequence(d, d-1, by = -1)
length(vec) <- length(int)
vec
}
Output
int = c(1, 1, 0, 5, 2, 0, 0, 2)
char = c("A", "B", "C", "A", "A")
f(int, 0)
# [1] 2 1 0 2 1 0 0 NA
f(int, 1)
# [1] 0 0 NA NA NA NA NA NA
f(int, 2)
# [1] 4 3 2 1 0 2 1 0
f(char, "A")
# [1] 0 2 1 0 0
Benchmark (n = 1000):
set.seed(123)
int = sample(0:100, size = 1000, replace = T)
library(microbenchmark)
bm <- microbenchmark(
fSequence(int, 0),
fzx8754(int, 0),
fRecursive(int, 0),
fMartinMorgan(int, 0),
fMap2dbl(int, 0),
fReduce(int, 0),
fAve(int, 0),
fjblood94(int, 0),
times = 10L,
setup = gc(FALSE)
)
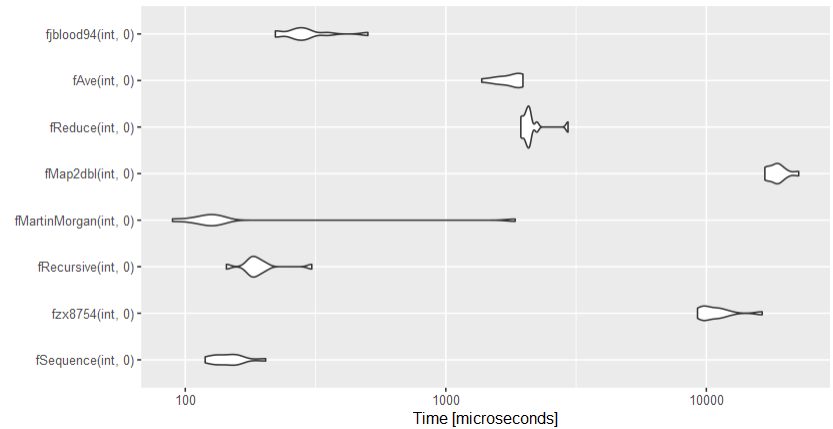
autoplot(bm)
Martin Morgan's solution seems to be the quickest, followed by this answer's sequence solution, sbarbit's recursive solution, and jblood94's for loop solution.
![enter image description here]()
Functions used:
fSequence <- function(v, x){
vec <- sequence(diff(c(0, which(v == x))), diff(c(0, which(v == x))) - 1, by = -1)
length(vec) <- length(v)
vec
}
fzx8754 <- function(v, x){
sapply(seq_along(v), function(i){
which(v[ i:length(v) ] == x)[ 1 ] - 1
})
}
fRecursive <- function(lookup,val ) {
ind <- which(lookup == val)[1] -1
if (length(lookup) > 1) {
c(ind, f(lookup[-1], val))
} else {
ind
}
}
fMartinMorgan <- function(x, value) {
idx = which(x == value)
nearest = rep(NA, length(x))
nearest[1:max(idx)] = rep(idx, diff(c(0, idx)))
abs(seq_along(x) - nearest)
}
fMap2dbl <- function(int, num)
{
n <- length(int)
map2_dbl(num, 1:n, ~ ifelse(length(which(.x == int[.y:n])) == 0, NA,
min(which(.x == int[.y:n])) - 1))
}
fReduce <- function(vec, value) {
replace(
Reduce(
function(x, y)
x + (y * x) ,
vec != value,
right = TRUE,
accumulate = TRUE
),
max(tail(which(vec == value), 1), 0) < seq_along(vec),
NA
)
}
fAve <- function(init, k) {
ave(
seq_along(init),
c(0, head(cumsum(init == k), -1)),
FUN = function(x) if (any(x == k)) rev(seq_along(x) - 1) else NA
)
}
fjblood94 <- function(v, val) {
out <- integer(length(v))
if (v[length(v)] != val) out[length(v)] <- NA_integer_
for (i in (length(v) - 1L):1) {
if (v[i] == val) {
out[i] <- 0L
} else {
out[i] <- out[i + 1L] + 1L
}
}
return(out)
}

fshould return the closest following value that equals "A". So first the value of char, "A", this is 0, for the second, it is 2, because B is 2-position away from the following "A" (4-2 = 2). Does it make more sense now? – Stroman