3ds max to C++/DirectX application orientation conversion

I want to export object from 3ds max to my C++/DirectX application and I have an problem with orientation exporting.

3ds max uses right-handed Z-up coordinate system and my application makes use of left-handed Y-up coordinate system. I use {x, y, z, w} notation of components in this whole question.

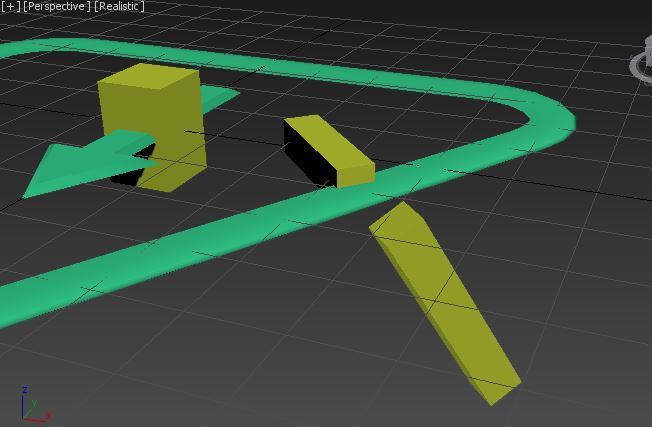
I have 3 bones (or any other hierarchical objects) in 3ds max:

To export their orientation I use MaxScript:

if hasParent then
    localOrientation = boneNode.transform.rotationPart * inverse boneNode.parent.transform.rotationPart
else
    localOrientation = boneNode.transform.rotationPart

I save this localOrientation to file:

BoneRoot no_parent 0.707107 0.0 0.0 0.707107 //stands for (-90, 0, 0) Euler rotation in 3ds max UI    
Bone001 BoneRoot 0.0 -0.382683 0.0 0.92388 //local orientation (parent space)
Bone002 Bone001 -0.353553 -0.612372 0.353553 -0.612372

I've read that despite 3ds max sing right-handed coordinate system, it uses left-handed system for transform.rotationPart.

My question is, how to now convert the local rotation from that file to my application? Maybe I should apply some conversion to root bone only? I have tried apply this to each bone orientation:

Quaternion convertFrom3dsMax(const Quaternion &input) {
auto q = input;
//swap Y and Z
auto temp = q.getZ();
q.setZ(q.getY());
q.setY(temp);

//invert
//q.setX(-q.getX());
q.setY(-q.getY());
q.setZ(-q.getZ());
q.setW(-q.getW());
return q;
}

And many other combinations of swaping axes, inverting arguments and even leaving everything as is. But each and every way my imported file bones are oriented in a wrong way.

Additional information (if needed):

My 3ds max scene looks like this:

And my application (for the convertFrom3dsMax function I presented; don't focus on mesh which is just an helper, look at lines that represent bones): 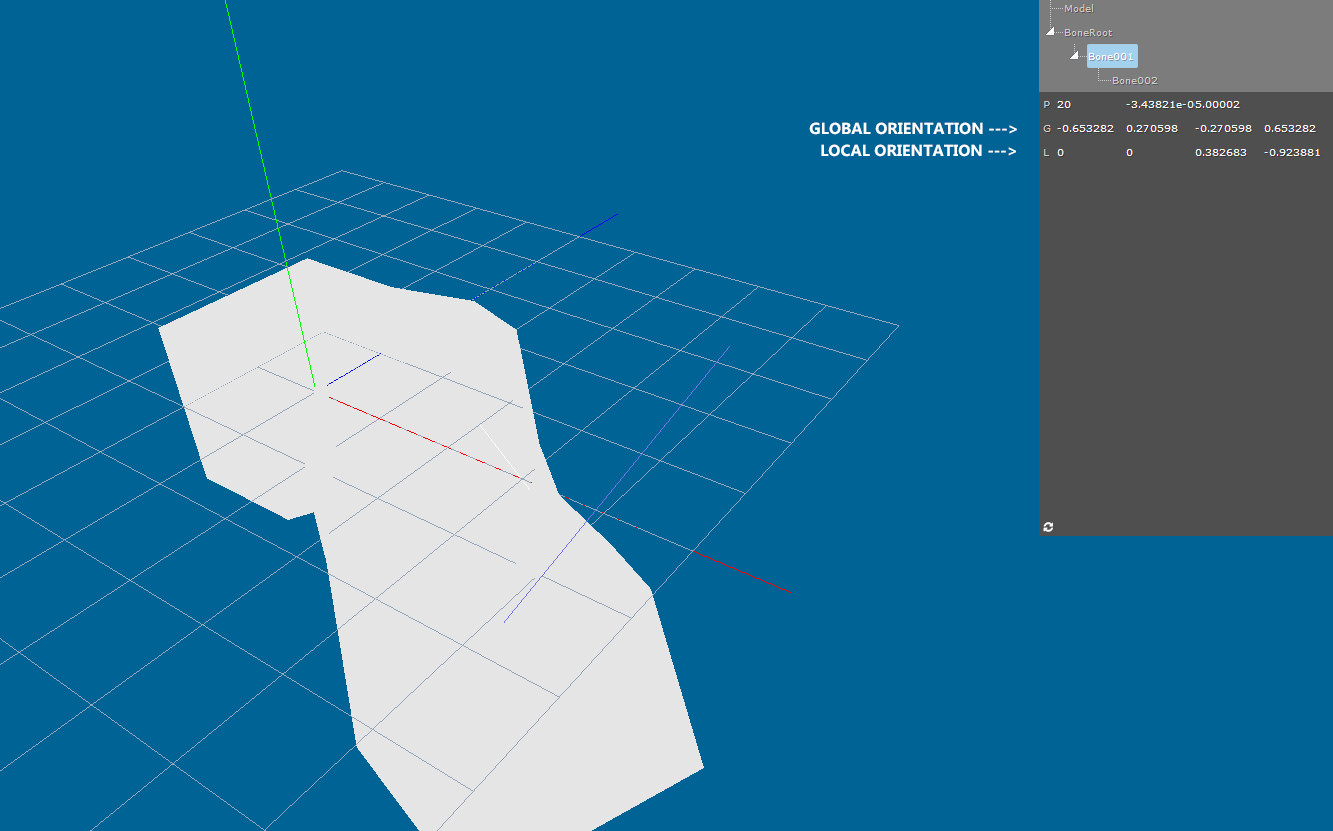(for example, but not only, the last bone is going "up" instead of "down")

When I don't apply anything to loaded Quaterions in my convertFrom3dsMax the scene looks this way: 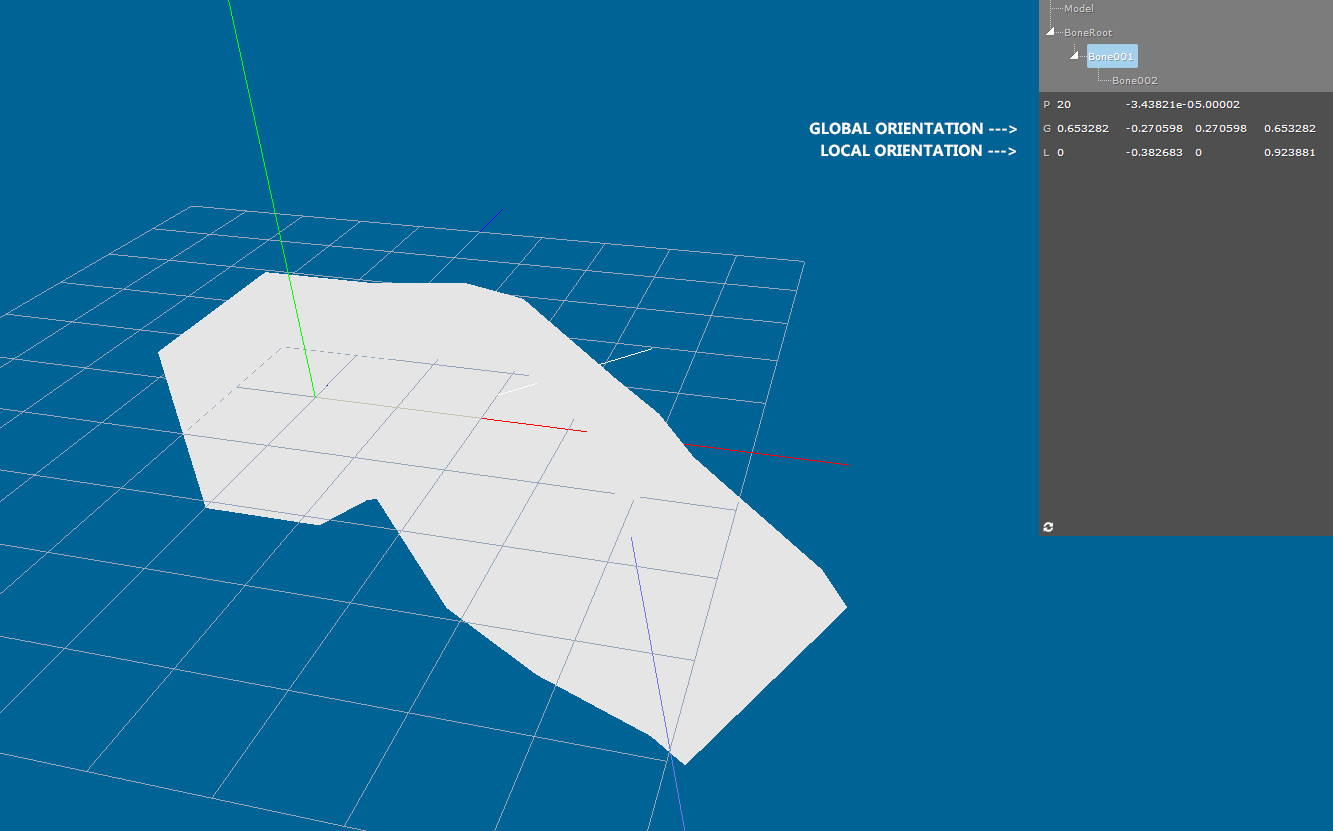(for example, but not only, the middle bone is going "from" instead of "to" the screen)

Note that I use left-handed operations for DirectX in my application (e.g. XMMatrixLookAtLH(...)) and I treat Y as "up".

Rotation matrix in application:

DirectX::XMMATRIX rotationMatrix = DirectX::XMMatrixRotationQuaternion(
    DirectX::XMVectorSet(
        object->global.getX(),
        object->global.getY(),
        object->global.getZ(),
        object->global.getW()
    )
);

And the global orientation is calculated this way: global = local * parent->global where local is loaded for each bone from file (with a help from convertFrom3dsMax) and operator* is defined as:

Quaternion operator* (const Quaternion by) const {
    //"R" for result
    float wR = w * by.getW() - x * by.getX() - y * by.getY() - z * by.getZ();
    float xR = x * by.getW() + w * by.getX() + y * by.getZ() - z * by.getY();
    float yR = y * by.getW() + w * by.getY() + z * by.getX() - x * by.getZ();
    float zR = z * by.getW() + w * by.getZ() + x * by.getY() - y * by.getX();
    return Quaternion(xR, yR, zR, wR);
}

I highly consider the convertFrom3dsMax as the source of my problems (and not the Quaternion math or DirectX calls inside of application).

For position, which is not that tricky as orientation I use boneNode.transform.pos and:

Point3D convertFrom3dsMax(const Point3D &input) {
auto result = input;
    //swap Y and Z
auto tempZ = result.getZ();
result.setZ(result.getY());
result.setY(tempZ);
return result;
}

which looks just right (the starting position of each line/Bone is ok, position of un-rotated helper mesh vertices are ok).

With 3DS using RH Z-Up and you are using LH Y up. The easiest thing to do is ignore your x-axis since it doesn't change; just copy the data over. You need to swap 3DS's Up - Z with your Y - Up. After the swap of these two axis, then what you need to do is invert the Z after the swap; that is due to the fact that a LH system the +z is coming out of the screen towards you.

Example:

3DS Max point in a RHS as being [Right (+x), Up (+z), Forward (+y)] and with your LHS [Right (+x), Up (+y) and Forward(-z)]. So if you have a vertex or a point in a RHS system such as [3,4,5] when you convert to your LHS system the point should now be [3,5,-4]. Assuming that +Z in your LHS is coming out of the screen.

I don't think you should have to worry about converting individual parts; I think the entire model or its root transform node needs to be converted by that convention.

So it should look something like this:

mat4 convertRHStoLHS( mat4 model ) {
    mat 4 newModel;
    newModel.x = model.x;   // Where X is X-Axis
    newModel.y = model.z;   //       Y is Y-Axis & Z is Z-Axis
    newModel.z = -model.y;  //       Z is Z-Axis & Y is Y-Axis

    return newModel;
}

Where mat4 would be your model's model transform matrix in model space.

Additional information (if needed):

Recommended topics

Hot tags