Sudoku solving in c++

Question

I've recently been working on a sudoku game in c++. I've made a graphic version of it using SFML and it works just fine. However, I need to implement an algorithm which will solve the sudoku, whilst not being a brute-force algorithm (so backtracking doesn't work for me ;/). I've read about many ways to solve it and I've come across different algorithm names (such as Dancing Links), as well as algorithms which only describe how the search works without giving any specific pieces of information on how to implement it in c++. (i.e. assigning a table or a list of possible numbers to each single "bucket" and searching for the solution, also someone mentioned so-called A* algorithm?)

So here is my question, what kind of algorithm is fairly easy to implement and is not the backtracking one? And where to find specific pieces of information on how to use it in c++? Thanks in advance. My program works on a two-dimensional array, but I could somehow make the buckets into structures if needed.

Stodgy

Here have a list: en.wikipedia.org/wiki/Sudoku_solving_algorithms – Garibold

You mostly have to solve it as you do as human. – Fender

Throw the algorithms away and figure it out for yourself. You may not achieve the optimum results (although you might, or even improve on them) but you'll learn a lot more. – Bollix

Such idea crossed my mind. I've decided to do something on my own, but that requires much work and my deadline is tomorrow. If it turns out that my idea is wrong, I'll be left with nothing, thus I decided to ask a question here. – Stodgy

@Stodgy added answer with some aditional rules I am using and code example – Orchidectomy

Why are you avoiding backtracking? Is this a school assignment where it's prohibited? Dancing links makes it straightforward. – Sofiasofie

Answer 1

Peter Norvig recommends using process of elimination (constraint propagation) followed by search. His article here provides a very thorough explanation.

In constraint propagation you use the following strategy:

(1) If a square has only one possible value, then eliminate that value from the square's peers. 
(2) If a unit has only one possible place for a value, then put the value there.

Now, it's easy to find in O(N) time the initially-filled squares in the puzzle. Put them all in a queue. If their neighbours, after propagating the constraint, have only a single value, add that to the queue. Repeat until the queue is empty.

The puzzle is now either solved or no further progress can be made by propagating constraints.

If the puzzle is not solved, you could either use a fancier algorithm or, as Norvig recommends, employ backtracking. Since the backtracking is being performed on a typically-small subset of the puzzle space, you're not using brute-force.

Evaporimeter

So does it work in a way that it separates all possible insertions that do not collide with anything and then tries inserting their combinations? – Stodgy

But how do I store that information? Should I make all the buckets into structures and create i.e. bool arrays which tell me that a number is good to use? Or is there a more elegant solution? – Stodgy

@Raf.M: Only you can decide what is best for you. But, to me, that sounds like a decent solution. You could also use std::bitset. – Evaporimeter

So I've decided to copy the values of my sudoku table into values of a node array, which - apart from int value; has bool *array;. Now I'm trying to write a function which will check whether a newly entered value would collide with anything, then - if that function returns false - I'd change the bool statement of corresponding number to true. Does that sound like a good plan? – Stodgy

@Raf.M: It sounds like it could work. I'm non-committal about whether it is good. – Evaporimeter

@Spektre: I worry that the rules you mention do not actually reduce the search space significantly and that your claim that they lead to fast solutions is not empirical. Backtracking will require the same code regardless of how many rules are used before it. So the best choice is likely to implement the simplest rule set (elimination) and then to test speed. In the article I link this produces results fairly quickly. – Evaporimeter

@Evaporimeter backtracking is form of genere&test usually recursive... the rules are heuristic for iterative deterministic method (no stepping back). just have coded the #1,#2 in C++ and it already lead to solution for hard difficulty sudoku... the solver itself is ~70 lines of C++ code no optimizations yet (probably will not bother as it is finished quicker than i release the button ...) Want to code the other rules then will post as an answer here ... PS in my experience the rules in worse case lead to 3-8 empty spaces but I saw only 3 sudokus that was not solved imediately by this – Orchidectomy

@Evaporimeter I finished editing my answer with the rules and solver description and full code included. – Orchidectomy

@Spektre: Backtracking is guaranteed to find a solution, if there is one. Rule-based methods are not, though applying advanced rules can reduce the search space. There 6.67e21 valid sudoku configurations. I appreciate having a method that is guaranteed to solve them all, rather than just an unknown fraction of them. – Evaporimeter

Answer 2

Description

Mine Sudoku is stored in form of 2D array 9x9 of 32 bit unsigned integers where each bit has its own purpose. low 10 bits are reserved for placed numbers (9 bits are used) next 10 bits are reserved for possible numbers (which can be placed there... which have not been ruled out yet) and finally one bit telling its a fixed cell and one telling if an error is present (conflict with another cell(s)).

As you can imagine my code boils down to bunch of binary operations ... which brings some problems on its own but solves others ...

Solver

As mentioned in the comments I am using rules and deterministic approach for this (no backtracking). The algo is like this:

1. compute checksum of sudoku
2. apply rules
3. compute checksum of sudoku
4. while the checksum is different than the last one loop to #2
5. check for errors

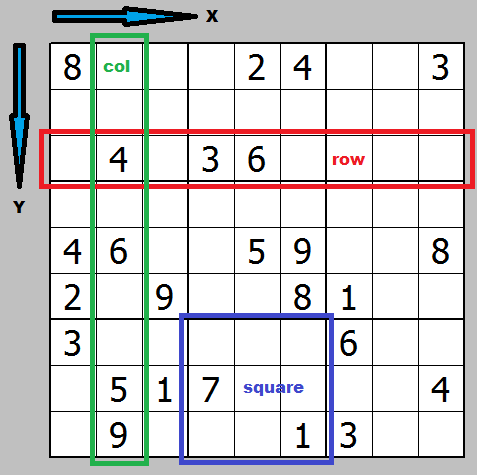
Terminology and conventions

the board is addressed by:

x = <0,9)
y = <0,9)

Now the rules:

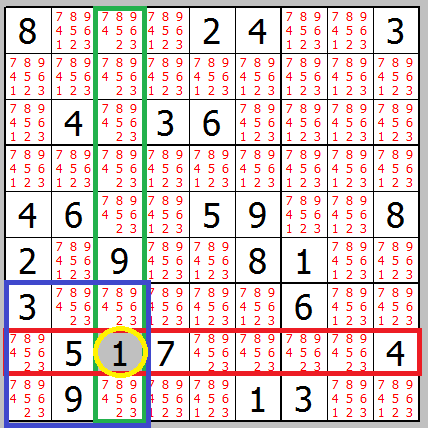
1. singleton must be unique along row/col/sqr

   so if we got cell with only single placed value then there is no chance another such value will appear in the same row/col/sqr so clear it like in this example:

2. if we got cell with only one possible number left place it

   that is simple if we cleared enough possible numbers from other rules sometimes we will be left with only one choice. Once detected place it and the cell is done ...

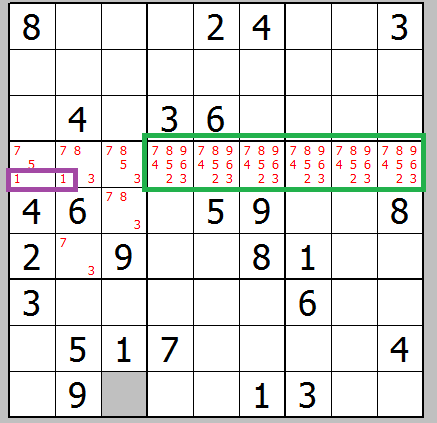
3. the same possible number only in single row/col for single square

   if found clear the row/col for other squares as they can not have another placement of such number.

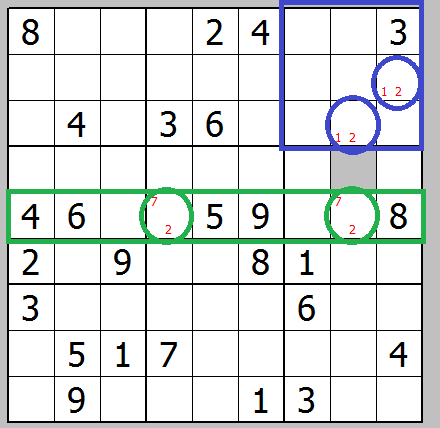
4. same pair found in single row/col/sqr

   if detected clear the rest. Beware the pair must be exactly the same (no other possible numbers may be present in the cell)

   this rule can be expanded to 3 triplets etc but never saw any opportunity to do so as the basic rules solve them before and their probability is low ...

Here small C++/VCL code for this (rule #4 is not implemented yet):

//---------------------------------------------------------------------------
#ifndef _sudoku_h
#define _sudoku_h
//---------------------------------------------------------------------------
// set numbers
const DWORD _sudoku_1     =(1<< 0); // set numbers (used)
const DWORD _sudoku_a1    =(1<<10); // possible numbers (unused)
const DWORD _sudoku_fix   =(1<<20); // read only?
const DWORD _sudoku_err   =(1<<21); // error?
const DWORD _sudoku_2=(_sudoku_1<<1);
const DWORD _sudoku_3=(_sudoku_1<<2);
const DWORD _sudoku_4=(_sudoku_1<<3);
const DWORD _sudoku_5=(_sudoku_1<<4);
const DWORD _sudoku_6=(_sudoku_1<<5);
const DWORD _sudoku_7=(_sudoku_1<<6);
const DWORD _sudoku_8=(_sudoku_1<<7);
const DWORD _sudoku_9=(_sudoku_1<<8);
const DWORD _sudoku_n=_sudoku_1|_sudoku_2|_sudoku_3|_sudoku_4|_sudoku_5|_sudoku_6|_sudoku_7|_sudoku_8|_sudoku_9;
const DWORD _sudoku_a2=(_sudoku_a1<<1);
const DWORD _sudoku_a3=(_sudoku_a1<<2);
const DWORD _sudoku_a4=(_sudoku_a1<<3);
const DWORD _sudoku_a5=(_sudoku_a1<<4);
const DWORD _sudoku_a6=(_sudoku_a1<<5);
const DWORD _sudoku_a7=(_sudoku_a1<<6);
const DWORD _sudoku_a8=(_sudoku_a1<<7);
const DWORD _sudoku_a9=(_sudoku_a1<<8);
const DWORD _sudoku_an=_sudoku_a1|_sudoku_a2|_sudoku_a3|_sudoku_a4|_sudoku_a5|_sudoku_a6|_sudoku_a7|_sudoku_a8|_sudoku_a9;
//---------------------------------------------------------------------------
class sudoku
    {
public:
    DWORD map[9][9];
    Graphics::TBitmap *bmp;
    bool _redraw,_render_an;

    int x0,y0;          // grid start
    int x1,y1;          // grid end
    int sz;             // grid size
    int yb;             // y of buttons panel
    int selx,sely,selb; // mouse selection
    TShiftState sh0;

    int _debug_N;

    sudoku();
    sudoku(sudoku& a)   { *this=a; }
    ~sudoku();
    sudoku* operator = (const sudoku *a) { *this=*a; return this; }
//  sudoku* operator = (const sudoku &a) { ...copy... return this; }

    // GUI/interface
    void init(int *S);              // init with linear mapped 1D array 0 is empty space, 1..9 is fixed cell
    void draw();
    void resize(int xs,int ys);
    void mouse(int mx,int my,TShiftState sh);
    void key(WORD key,TShiftState sh);
    void load(AnsiString filename);
    void save(AnsiString filename);
    void set(int x,int y,DWORD m);  // set map[x][y]|=m
    void rst(int x,int y,DWORD m);  // clear map[x][y]-=m
    void xor(int x,int y,DWORD m);  // xor map[x][y]^=m
    // solver
    void s_init();                  // reset/init state from fixed cells only
    void s_check();                 // check for errors
    void solve();                   // solve the puzzle from scratch
    };
//---------------------------------------------------------------------------
sudoku::sudoku()
    {
    int i,j;
    _render_an=false;
    _redraw=false;
    selx=-1;
    sely=-1;
    selb=-1;
    bmp=new Graphics::TBitmap;
    for (i=0;i<9;i++)
     for (j=0;j<9;j++)
      map[i][j]=0;
    }
//---------------------------------------------------------------------------
sudoku::~sudoku()
    {
    if (bmp) delete bmp; bmp=NULL;
    }
//---------------------------------------------------------------------------
void sudoku::init(int *S)
    {
    int x,y,a;
    for (a=0,y=0;y<9;y++)
     for (x=0;x<9;x++,a++)
      if (S[a]) map[x][y]=(_sudoku_1<<(S[a]-1))|_sudoku_fix;
       else map[x][y]=0;
    s_init();
    _debug_N=0;
    }
//---------------------------------------------------------------------------
void sudoku::draw()
    {
    if (bmp==NULL) return;
    AnsiString s;
    int i,j,k,x,y;
    DWORD a;
    // clear
    bmp->Canvas->Brush->Color=clLtGray;
    bmp->Canvas->Brush->Style=bsSolid;
    bmp->Canvas->FillRect(Rect(0,0,bmp->Width,bmp->Height));
    bmp->Canvas->Brush->Color=clWhite;
    bmp->Canvas->FillRect(Rect(x0,y0,x1,y1));
    // selection
    if ((selx>=0)&&(selx<9))
     if ((sely>=0)&&(sely<9))
        {
        x=x0+(selx*sz);
        y=y0+(sely*sz);
        bmp->Canvas->Brush->Color=clSilver;
        bmp->Canvas->FillRect(Rect(x,y,x+sz,y+sz));
        }
    // buttons
    bmp->Canvas->Pen  ->Width=2;
    bmp->Canvas->Brush->Color=clWhite;
    bmp->Canvas->FillRect(Rect(x0,yb,x1,yb+sz));
    if ((selb>=0)&&(selb<9))
        {
        x=x0+(selb*sz);
        bmp->Canvas->Brush->Color=clDkGray;
        bmp->Canvas->FillRect(Rect(x,yb,x+sz,yb+sz));
        }
    for (j=0,i=0;i<=9;i++,j+=sz)
        {
        bmp->Canvas->MoveTo(x0+j,yb);
        bmp->Canvas->LineTo(x0+j,yb+sz);
        }
    bmp->Canvas->MoveTo(x0,yb);
    bmp->Canvas->LineTo(x1,yb);
    bmp->Canvas->MoveTo(x0,yb+sz);
    bmp->Canvas->LineTo(x1,yb+sz);
    // major grid
    bmp->Canvas->Pen  ->Color=clBlack;
    for (j=0,i=0;i<=3;i++,j+=3*sz)
        {
        bmp->Canvas->MoveTo(x0,y0+j);
        bmp->Canvas->LineTo(x1,y0+j);
        bmp->Canvas->MoveTo(x0+j,y0);
        bmp->Canvas->LineTo(x0+j,y1);
        }
    // minor grid
    bmp->Canvas->Pen  ->Width=1;
    for (j=0,i=0;i<9;i++,j+=sz)
        {
        bmp->Canvas->MoveTo(x0,y0+j);
        bmp->Canvas->LineTo(x1,y0+j);
        bmp->Canvas->MoveTo(x0+j,y0);
        bmp->Canvas->LineTo(x0+j,y1);
        }
    // big numbers
    bmp->Canvas->Brush->Style=bsClear;
    bmp->Canvas->Font->Height=sz-4;
    for (i=0;i<9;i++)
     for (j=0;j<9;j++)
        {
        a=map[i][j]; if (_render_an) a>>=10; a&=_sudoku_n; if (!a) continue;
             if (DWORD(map[i][j]&_sudoku_err)!=0) bmp->Canvas->Font->Color=clRed;
        else if (DWORD(map[i][j]&_sudoku_fix)!=0) bmp->Canvas->Font->Color=clBlack;
        else                                      bmp->Canvas->Font->Color=clBlue;
        for (k=0;k<9;k++)
         if (a==(_sudoku_1<<k))
            {
            s=k+1;
            x=x0+(i*sz)+((sz-bmp->Canvas->TextWidth (s))>>1);
            y=y0+(j*sz)+((sz-bmp->Canvas->TextHeight(s))>>1);
            bmp->Canvas->TextOutA(x,y,s);
            break;
            }
        }
    // small numbers
    bmp->Canvas->Brush->Style=bsClear;
    i=(sz-4)/3;
    const int dx[9]={-i,0,+i,-i,0,+i,-i,0,+i};
    const int dy[9]={+i,+i,+i,0,0,0,-i,-i,-i};
    bmp->Canvas->Font->Height=i;
    for (i=0;i<9;i++)
     for (j=0;j<9;j++)
        {
        a=map[i][j]; if (_render_an) a>>=10; a&=_sudoku_n; if (!a) continue;
        for (k=0;k<9;k++) if (a==(_sudoku_1<<k)) { k=-1; break; } if (k<0) continue;
             if (DWORD(map[i][j]&_sudoku_fix)!=0) bmp->Canvas->Font->Color=clBlack;
        else if (DWORD(map[i][j]&_sudoku_err)!=0) bmp->Canvas->Font->Color=clRed;
        else                                      bmp->Canvas->Font->Color=clBlue;
        for (k=0;k<9;k++)
         if (DWORD(a&(_sudoku_1<<k))!=0)
            {
            s=k+1;
            x=x0+(i*sz)+((sz-bmp->Canvas->TextWidth (s))>>1)+dx[k];
            y=y0+(j*sz)+((sz-bmp->Canvas->TextHeight(s))>>1)+dy[k];
            bmp->Canvas->TextOutA(x,y,s);
            }
        }
    // info
    x=5; y=5; i=20; y-=i;
    bmp->Canvas->Font->Color=clBlack;
    bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("N:%i",_debug_N));
    bmp->Canvas->TextOutA(x,y+=i,AnsiString().sprintf("%ix%i",selx,sely));
    if (_render_an) bmp->Canvas->TextOutA(x,y+=i,"an");

    // button numbers
    bmp->Canvas->Font->Height=sz-4;
    a=0;
    if ((selx>=0)&&(selx<9))
     if ((sely>=0)&&(sely<9))
      a=map[selx][sely]&_sudoku_n;
    for (i=0;i<9;i++)
        {
        s=i+1;
        x=x0+(i*sz)+((sz-bmp->Canvas->TextWidth (s))>>1);
        y=yb       +((sz-bmp->Canvas->TextHeight(s))>>1);
        if (DWORD(a&(_sudoku_1<<i))!=0) bmp->Canvas->Font->Color=clBlack;
        else                            bmp->Canvas->Font->Color=clLtGray;
        bmp->Canvas->TextOutA(x,y,s);
        }
    bmp->Canvas->Brush->Style=bsSolid;
    }
//---------------------------------------------------------------------------
void sudoku::resize(int xs,int ys)
    {
    bmp->SetSize(xs,ys);
    _redraw=true;
    int w=8;
    x0=(xs-w-w  )/ 9;
    y0=(ys-w-w-w)/10;
    sz=x0; if (sz>y0) sz=y0;
    x0=(xs-( 9*sz))/2;
    y0=(ys-(10*sz)-w)/2;
    x1=x0+(9*sz);
    y1=y0+(9*sz);
    yb=y1+w;
    }
//---------------------------------------------------------------------------
void sudoku::mouse(int mx,int my,TShiftState sh)
    {
    int q0=sh0.Contains(ssLeft);
    int q1=sh .Contains(ssLeft);
    if ((mx< x0)||(mx>=x1)) return;
    if ((my>=y0)&&(my< y1))
     if ((!q0)&&(q1))
        {
        selx=(mx-x0)/sz;
        sely=(my-y0)/sz;
        _redraw=true;
        }
    if ((my>=yb)&&(my< yb+sz))
        {
        selb=(mx-x0)/sz;
        _redraw=true;
        if ((!q0)&&(q1))
         if ((selx>=0)&&(selx<9))
          if ((sely>=0)&&(sely<9))
           xor(selx,sely,_sudoku_1<<selb);
        }
    else{
        _redraw|=selb!=-1;
        selb=-1;
        }
    sh0=sh;
    }
//---------------------------------------------------------------------------
void sudoku::key(WORD key,TShiftState sh)
    {
    // toggle (un)used number
    int a=-1;
    if ((key>='1')&&(key<='9')) a=key-'1';                  // 0..9
    if ((key>=97)&&(key<=105)) a=key-97;                    // num0..num9
    if (a>=0)
     if ((selx>=0)&&(selx<9))
      if ((sely>=0)&&(sely<9))
        {
        if (_render_an) a+=10;
        xor(selx,sely,_sudoku_1<<(a));
        }
    // navigate selection cell
    if ((key>=37)&&(key<=40))                               // arrows
        {
        if (key==37) { selx--; _redraw=true; }
        if (key==39) { selx++; _redraw=true; }
        if (key==38) { sely--; _redraw=true; }
        if (key==40) { sely++; _redraw=true; }
        if (selx<0) selx=0; if (selx>8) selx=8;
        if (sely<0) sely=0; if (sely>8) sely=8;
        }
    if (key== 27) { _redraw=true; selx=-1; sely=-1; }       // esc      clear selection
    if (key== 32) { solve(); }                              // space    apply solving rules
    if (key==112) { _redraw=true; _render_an=!_render_an; } // F1       used/unused numbers mode
    if (key==113) { _redraw=true; save("map000.dat"); }     // F2       save
    if (key==116) { _redraw=true; load("map000.dat"); }     // F5       load
    if (key==119) { _redraw=true; s_init();  }              // F8       restart
    // debug
    if (key==107) { _debug_N++; solve(); }                  // num+
    if (key==109) { _debug_N--; solve(); }                  // num-
    }
//---------------------------------------------------------------------------
void sudoku::load(AnsiString filename)
    {
    int hnd,x,y;
    hnd=FileOpen(filename,fmOpenRead);
    if (hnd<0) return;
    for (x=0;x<9;x++)
     for (y=0;y<9;y++)
      FileRead(hnd,&map[x][y],sizeof(map[0][0]));
    FileClose(hnd);
    _redraw=true;
    }
//---------------------------------------------------------------------------
void sudoku::save(AnsiString filename)
    {
    int hnd,x,y;
    hnd=FileCreate(filename);
    if (hnd<0) return;
    for (x=0;x<9;x++)
     for (y=0;y<9;y++)
      FileWrite(hnd,&map[x][y],sizeof(map[0][0]));
    FileClose(hnd);
    }
//---------------------------------------------------------------------------
void sudoku::set(int x,int y,DWORD m)
    {
    if ((x<0)||(x>=9)||(y<0)||(y>=9)) return;
    if (DWORD(map[x][y]&m)!=0) return;
    if (DWORD(map[x][y]&_sudoku_fix)!=0) return;
    map[x][y]|=m;
    s_check();
    _redraw=true;
    }
//---------------------------------------------------------------------------
void sudoku::rst(int x,int y,DWORD m)
    {
    if ((x<0)||(x>=9)||(y<0)||(y>=9)) return;
    if (DWORD(map[x][y]&m==0)) return;
    if (DWORD(map[x][y]&_sudoku_fix)!=0) return;
    map[x][y]|=m;
    map[x][y]^=m;
    s_check();
    _redraw=true;
    }
//---------------------------------------------------------------------------
void sudoku::xor(int x,int y,DWORD m)
    {
    if ((x<0)||(x>=9)||(y<0)||(y>=9)) return;
    if (DWORD(map[selx][sely]&m)==0) set(selx,sely,m);
     else                            rst(selx,sely,m);
    }
//---------------------------------------------------------------------------
void sudoku::s_init()
    {
    int x,y;
    DWORD a,b;
    for (x=0;x<9;x++)
     for (y=0;y<9;y++)
        {
        a=map[x][y];
        if (DWORD(a&_sudoku_fix)==0) a =_sudoku_an;
         else                      { a&=_sudoku_n|_sudoku_fix; a|=(a<<10)&_sudoku_an; }
        map[x][y]=a;
        }
    s_check();
    _redraw=true;
    }
//---------------------------------------------------------------------------
void sudoku::s_check()
    {
    int x,y,_x,_y,xx,yy,k,n[10];
    DWORD a,b,m[9][9];
    // iterate xx,yy through adjacent cells to x,y (included)
    #define row(y) for (yy=y,xx=0;xx<9;xx++)
    #define col(x) for (xx=x,yy=0;yy<9;yy++)
    #define sqr(x,y) for (_x=(x/3)*3,_y=(y/3)*3,xx=_x;xx<_x+3;xx++) for (yy=_y;yy<_y+3;yy++)
    // init m[][] with singleton used numbers from map[][] and clear error
    for (x=0;x<9;x++ ) for (y=0;y<9;y++ ){ m[x][y]=0; a=map[x][y]&_sudoku_n; map[x][y]&=0xFFFFFFFF^_sudoku_err; for (b=_sudoku_1,k=1;k<=9;k++,b<<=1)  if (a==b) m[x][y]=k; }
                                         // compute histogram n[]                                  // check for error (count>1) and flag it for rendering
                       for (y=0;y<9;y++ ){ for (xx=0;xx<=9;xx++) n[xx]=0; row(  y) n[m[xx][yy]]++; n[0]=0; row(  y) if (n[m[xx][yy]]>1) map[xx][yy]|=_sudoku_err; }
    for (x=0;x<9;x++ )                   { for (xx=0;xx<=9;xx++) n[xx]=0; col(x  ) n[m[xx][yy]]++; n[0]=0; col(x  ) if (n[m[xx][yy]]>1) map[xx][yy]|=_sudoku_err; }
    for (x=0;x<9;x+=3) for (y=0;y<9;y+=3){ for (xx=0;xx<=9;xx++) n[xx]=0; sqr(x,y) n[m[xx][yy]]++; n[0]=0; sqr(x,y) if (n[m[xx][yy]]>1) map[xx][yy]|=_sudoku_err; }
    #undef row
    #undef col
    #undef sqr
    }
//---------------------------------------------------------------------------
void sudoku::solve()
    {
    int k,n[9],nx[9],ny[9];
    DWORD a,b;

    int x,y,_x,_y,xx,yy;
    DWORD checksum0,checksum;
    // is a single bit set from _sudoku1.._sudoku_9?
    #define single(a) for (b=_sudoku_1;b<=_sudoku_9;b<<=1) if (a==b)
    // iterate xx,yy through adjacent cells to x,y (included)
    #define row(y) for (yy=y,xx=0;xx<9;xx++)
    #define col(x) for (xx=x,yy=0;yy<9;yy++)
    #define sqr(x,y) for (_x=(x/3)*3,_y=(y/3)*3,xx=_x;xx<_x+3;xx++) for (yy=_y;yy<_y+3;yy++)

    s_init();

    // solve main loop
    for (checksum0=0,_debug_N=0;;_debug_N++)
        {
        // compute checksum and stop if not changed
        for (checksum=0,a=1,x=0;x<9;x++)
         for (y=0;y<9;y++,a++)
          checksum+=map[x][y]&(_sudoku_n|_sudoku_an)*a;
        if (checksum==checksum0) break;
        checksum0=checksum;

        // #1 clear singleton used numbers in (un)used numbers of adjacent cells
        for (x=0;x<9;x++)
         for (y=0;y<9;y++)
            {
            a=map[x][y]&_sudoku_n;
            single(a)
                {
                b=a<<10;
                map[x][y]&=0xFFFFFFFF^_sudoku_an;
                map[x][y]|=b;
                b^=0xFFFFFFFF;
                row(  y) if  (xx!=x)           map[xx][yy]&=b;
                col(x  ) if           (yy!=y)  map[xx][yy]&=b;
                sqr(x,y) if ((xx!=x)||(yy!=y)) map[xx][yy]&=b;
                break;
                }
            }

        // #2 find if just single occurence in adjacent cells
                                             // clear histogram n[]        compute histogram n[]                                                                                                                       // handle single occurence by clearing all other adjacent cells
                           for (y=0;y<9;y++ ){ for (xx=0;xx<9;xx++) n[xx]=0; row(  y) { a=map[xx][yy]; a=(a|(a>>10))&_sudoku_n; for (b=0;b<9;b++) if (DWORD(a&(_sudoku_1<<b))!=0) { n[b]++; nx[b]=xx; ny[b]=yy; }} for (b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (n[k]==1) row(  y) if (DWORD(map[xx][yy]&_sudoku_fix)==0) if ((xx==nx[k])&&(yy==ny[k])) map[xx][yy]&=0xFFFFFFFF^(_sudoku_n|_sudoku_an)^b; else map[xx][yy]&=0xFFFFFFFF^b; }
        for (x=0;x<9;x++ )                   { for (xx=0;xx<9;xx++) n[xx]=0; col(x  ) { a=map[xx][yy]; a=(a|(a>>10))&_sudoku_n; for (b=0;b<9;b++) if (DWORD(a&(_sudoku_1<<b))!=0) { n[b]++; nx[b]=xx; ny[b]=yy; }} for (b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (n[k]==1) col(x  ) if (DWORD(map[xx][yy]&_sudoku_fix)==0) if ((xx==nx[k])&&(yy==ny[k])) map[xx][yy]&=0xFFFFFFFF^(_sudoku_n|_sudoku_an)^b; else map[xx][yy]&=0xFFFFFFFF^b; }
        for (x=0;x<9;x+=3) for (y=0;y<9;y+=3){ for (xx=0;xx<9;xx++) n[xx]=0; sqr(x,y) { a=map[xx][yy]; a=(a|(a>>10))&_sudoku_n; for (b=0;b<9;b++) if (DWORD(a&(_sudoku_1<<b))!=0) { n[b]++; nx[b]=xx; ny[b]=yy; }} for (b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (n[k]==1) sqr(x,y) if (DWORD(map[xx][yy]&_sudoku_fix)==0) if ((xx==nx[k])&&(yy==ny[k])) map[xx][yy]&=0xFFFFFFFF^(_sudoku_n|_sudoku_an)^b; else map[xx][yy]&=0xFFFFFFFF^b; }

        // #3 if the same number only in single row/col for single square clear the row/col for other squares
        for (x=0;x<9;x+=3)
         for (y=0;y<9;y+=3)
            {
            // nx[],ny[] = histogram of x,y per each number
            for (xx=0;xx<9;xx++) { nx[xx]=0; ny[xx]=0; } sqr(x,y) for (a=map[xx][yy],b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (DWORD(a&b)!=0) { nx[k]|=1<<xx; ny[k]|=1<<yy; }
            // check row/col for exclusive occurence and clear the rest if found
            for (yy=y;yy<y+3;yy++) for (b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (ny[k]==1<<yy) for (xx=0;xx<9;xx++) if ((xx<x)||(xx>=x+3)) map[xx][yy]&=0xFFFFFFFF^b;
            for (xx=x;xx<x+3;xx++) for (b=_sudoku_1|_sudoku_a1,k=0;k<9;k++,b<<=1) if (nx[k]==1<<xx) for (yy=0;yy<9;yy++) if ((yy<y)||(yy>=y+3)) map[xx][yy]&=0xFFFFFFFF^b;
            }

        // #4 same pair only found in single row/col/sqr (clear the rest)
        // [***ToDo***]

        // set singleton unused numbers as used
        for (x=0;x<9;x++)
         for (y=0;y<9;y++)
            {
            a=(map[x][y]>>10)&_sudoku_n;
            single(a)
                {
                map[x][y]&=0xFFFFFFFF^_sudoku_n;
                map[x][y]|=a;
                break;
                }
            }
        }
    s_check();      
    _redraw=true;
    #undef single
    #undef row
    #undef col
    #undef sqr
    }
//---------------------------------------------------------------------------
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------

And usage:

//$$---- Form CPP ----
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include "Unit1.h"
#include "sudoku.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
sudoku gam;
//---------------------------------------------------------------------------
void TForm1::draw()
    {
    if (gam._redraw) gam.draw();
    Canvas->Draw(0,0,gam.bmp);
    }
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner):TForm(Owner)
    {
    int S[9*9]=
        {
        8,0,0, 0,2,4, 0,0,3,
        0,0,0, 0,0,0, 0,0,0,
        0,4,0, 3,6,0, 0,0,0,

        0,0,0, 0,0,0, 0,0,0,
        4,6,0, 0,5,9, 0,0,8,
        2,0,9, 0,0,8, 1,0,0,

        3,0,0, 0,0,0, 6,0,0,
        0,5,1, 7,0,0, 0,0,4,
        0,9,0, 0,0,1, 3,0,0,
        };
    gam.init(S);
    }
//---------------------------------------------------------------------------
void __fastcall TForm1::FormPaint(TObject *Sender) { draw(); }
void __fastcall TForm1::FormResize(TObject *Sender) { gam.resize(ClientWidth,ClientHeight); }
void __fastcall TForm1::tim_updTimer(TObject *Sender) { if (gam._redraw) draw(); }
void __fastcall TForm1::FormKeyDown  (TObject *Sender, WORD &Key, TShiftState Shift){ gam.key(Key,Shift); }
void __fastcall TForm1::FormMouseMove(TObject *Sender,                      TShiftState Shift, int X, int Y){ gam.mouse(X,Y,Shift); }
void __fastcall TForm1::FormMouseDown(TObject *Sender, TMouseButton Button, TShiftState Shift, int X, int Y){ gam.mouse(X,Y,Shift); }
void __fastcall TForm1::FormMouseUp  (TObject *Sender, TMouseButton Button, TShiftState Shift, int X, int Y){ gam.mouse(X,Y,Shift); }
//---------------------------------------------------------------------------

Its the code form my VCL app (single form with single timer on it) so just port the events to your environment and ignore the rest. The sudoku class uses VCL encapsulated GDI so that is the stuff that is need to be ported (just lines rectangles and text).

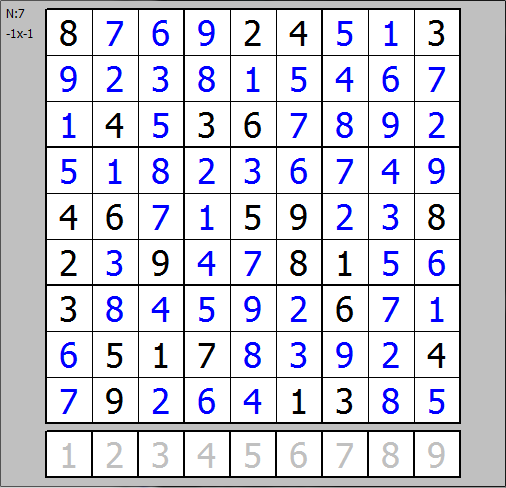
The solver is fully enclosed within sudoku::solve() and hope its commented enough (does exactly what I described above). Here screenshot after solving (space key):

the _debug_N (N:7) holds the count of iterations needed for solution. Also I did not do any optimizations yet (do not see any point as the solver is done sooner than i release the key). Hope this helps someone a bit.

There are quite a few other rules to implement:

• Sudoku Solving Strategies
• Sudoku Solving Techniques

Orchidectomy