How to Remove the ambiguity from the following grammar?

Question

Remove the ambiguity from the following grammar

S −−> if E then S | if E then S else S | other

Versed

Does this answer your question? LL(1) grammar for dangling else – Preachment

I don't think it does, because the referenced question discusses LL(1) parsing (determinism), not ambiguity. See my answer down. – Deliverance

Answer 1

You can remove the dangling-else ambiguity. There is such a grammar in "Compilers: Principles, Techniques, and Tools" 2th edition, page 211-212. However, the book has the grammar, but there is no explanation for it (or I have not found it).

In the ABNF meta syntax the grammar is:

statement = matched / open
matched   = "if" expr "then" matched "else" matched 
          / other
open      = "if" expr "then" statement
          / "if" expr "then" matched "else" open

expr      = ...
other     = ...

How does it work?

The idea here is to avoid the ambiguity by using non-determinism (that is anyway presented already, because every ambiguous grammar is also non-deterministic; in the end I wrote about the differences, that I find to be (too) often misunderstood). That means that after a successful parsing there is only one syntax tree possible for any input (meaning non-ambiguity as you requested). But you will need a parser that works with a more complex machinery than the deterministic LL(1) parsers.

Rule matched ensures that every directly nested if-statement inside the sub-tree will have else. With other words, the then will have a matched else.

Rule open ensures that every sub-if statement does not have else in itself, or if it does, then its else-statement is open in turn. With other words, rule open ensures that there will be less else keywords used than then keywords used. And with other words, the number of else inside the sub-tree will be less than the number of then (or ifs if you like). That is in a contrast to the matched rule that ensures an equal number of both. That means that matched and open, implemented in a parser, are never going to accept the same input, counting from the first usage of rule statement.

Additionally, because of matched "else" open in rule open, the else will be "attached" to the nearest if. This resolves the dangling-else ambiguity before the parser recognizes the first used statement.

Example

To illustrate the steps that are going to happen, I have upgraded the grammar to allow more "natural" input. That means more punctuation and white space. First the lexer:

keyword = %s"if" / %s"then" / %s"else"

It groups the input characters into groups when ever possible, and the non-grouped characters become tokens by themselves. For input of:

if(x)then if(x)then y else y

You have these bytes:

For these bytes, you will have these tokens:

Then you have the parser grammar that allows the parser to accept these tokens (case sensitively) and has white space explicitly placed. You can still watch the original one, the overall process is the same. The parser grammar:

statement = matched / open
matched   = {keyword, %s"if"} *ws "(" *ws expr *ws ")" *ws {keyword, %s"then"} 1*ws matched {keyword, %s"else"} 1*ws matched 
          / other *ws
open      = {keyword, %s"if"} *ws "(" *ws expr *ws ")" *ws {keyword, %s"then"} 1*ws statement
          / {keyword, %s"if"} *ws "(" *ws expr *ws ")" *ws {keyword, %s"then"} 1*ws matched {keyword, %s"else"} 1*ws open

expr      = %s"x"
other     = %s"y" 
ws        = %s" "

After you start the parsing, a parsing machine that explores in-depth the grammar rules, will perform in this way:

• it will enter in the start rule statement
• then into the first concatenation that has a reference to rule matched.
• it will accept the first tokens that have the characters if(x)then
• then it will again use the matched rule
• it will accept all other tokens till the end of the input if(x)then y else y.
• then will move out of the matched rule and will expect its matched else, but there is no such, because the input has ended. That means the parser must go back to search for another way. At this point in time you will have this (partially constructed) syntax tree:
• it will go back to the very beginning of the parsing and will try the second concatenation in rule statement, the one referencing rule open.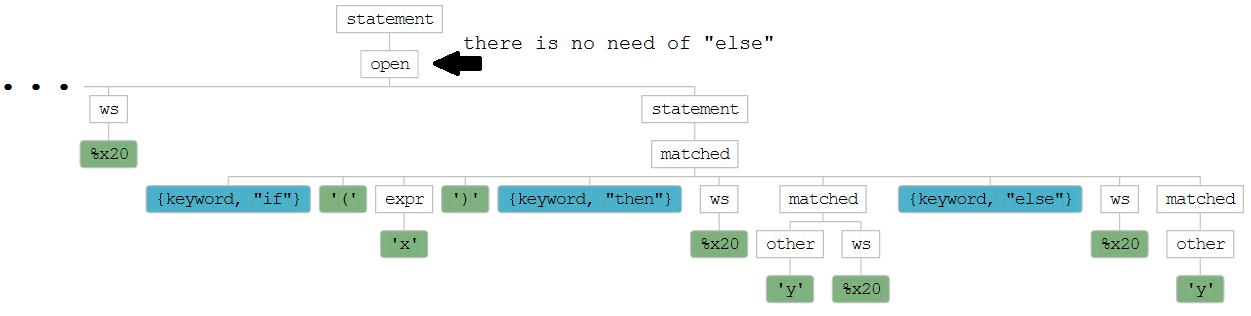
• it will work its steps and will eventually reach the end of the input successfully with this tree:
• then the parsing machine might continue to explore more, but will not find any other syntax trees.

Related Theory

It is often that determinism, non-determinism, ambiguity, and non-ambiguity are misunderstood. I would like to give an example of each, because I think that the written up might not be clear for everyone.

From the perspective of a parser, the determinism is related to the number of actions possible at a given state. When for all possible states in the parser at most one action is possible than the parser is deterministic. I have seen in many places the phrasing that "a grammar is mostly deterministic, and just in few places non-deterministic". That is misleading, because the determinism of a grammar is based on the whole grammar - more precisely its worst deterministic case. For example, the next grammar is deterministic, and when used by a parser, the parser will also be a deterministic one:

rule = "a" / "b"

Non-deterministic means that there is at least one possible state of the parser, where more than one action is possible, for at least one input sequence. For example, the following grammar is non-deterministic:

rule = "a" / "a" 

Clearly, you could rewrite it to just rule = "a" but that is not the same grammar. Both of the grammars just generate the same language. A grammar is generating the valid strings of a language. This language consists of its valid strings. A parser is accepting the valid language strings and it is rejecting the invalid ones.

Ambiguity means that the input can be recognized in more than one way. That in turn means that more than one syntax tree is possible for at least one valid input. For example, the previous grammar (rule = "a" / "a") is ambiguous, because both of the concatenations have a.

Non-ambiguous means that any valid input will be recognized in exactly one way. That in turn means that exactly one syntax tree exists for each valid input. Clearly for the invalid inputs there are no syntax trees.

You might have a grammar that is non-deterministic and non-ambiguous, like this one:

rule = "a" "b" / "a" "c"

You have a non-deterministic choice at the beginning of the rule for input character a, but in the next input character it will become clear which concatenation is the right one. It is not possible, after the input is fully processed to have more than one syntax tree: meaning the grammar is non-ambiguous.

Clearly, every deterministic grammar is also non-ambiguous, because there is no state where a second action is possible that could lead to a second tree.

Additionally, every ambiguous grammar is non-deterministic, because to be able to have more than one syntax tree, somewhere exists a state, that has more than one action possible, for at least one input sequence.

The "trick" of the book's grammar is that the non-determinism is let to exists (it is actually "employed"), but it is not let to propagate outside of the statement rule, to effectively prevent the grammar to become ambiguous.

Now, all of this is valid when the parser processes its input one character at a time. But I'm not going far from here. There are also different types of ambiguity. Some you can count, some you cannot. But I'm not going there as well.

Disclaimer: I have used screenshots and the grammar syntax of the tool I develop: Tunnel Grammar Studio.

Deliverance