Height/Elevation of a pixel from ground in Google Street View

Question

I am looking to find the height of every pixel from ground in the google street view.

Couple of things I know can be calculated are:

1. Pitch of a pixel

2. Depth map of every pixel from camera

   There is a javascript library to fetch depth map too.

Is it possible to put the two together to calculate actual height of a pixel from ground?

Autograft

Answer 1

If we know the height of the camera then this becomes a simple matter of trigonometry.

tan(angle) = height-above-camera / depth

so

height-above-camera = depth * tan(angle)

If the camera is known to be 8ft above ground then we can get the actual height of a pixel as

height = 8ft + depth * tan(angle)

The whole calculation depends on the quality of the depth map.

Another thing you could exploit is assuming the blocks in the depth map end at ground level. Then run an edge detection on the image.

Here I've used an online Canny Edge detection which is picking out the base of the block on the right-hand side. A bit of trig should get the height.

Better than using image processing if you allow interactive use, get the user to click on the base of the object and the top of the object. Knowing the pitch of the point at the base allows the distance to be calculated.

Practically

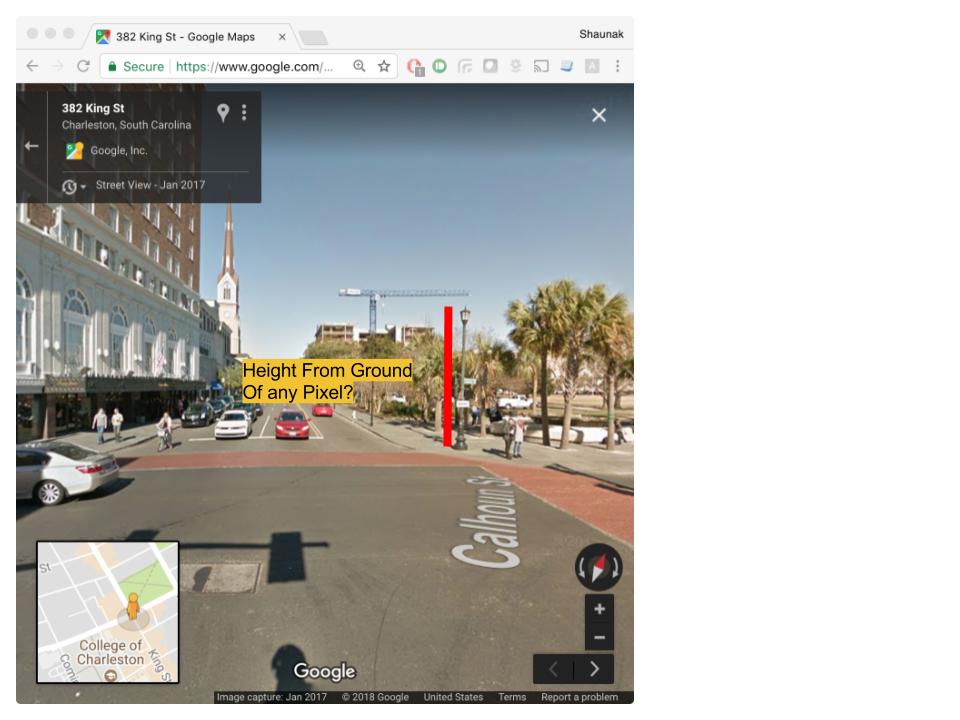
I probably miss something but how do you easily calculate or estimate angle or tan(angle)? – Natalya

It's just the pitch. – Practically

@Salixalba great answer! That can work. basically need height form ground of every pixel in the image. Can you please elaborate a little on "Height of camera" and "Height above camera"? I think the height of camera is fixed at 8ft. – Autograft

If we know the height of camera is 8ft then we know all pixels at 0° pitch must also be 8ft. I've updated the answer with this. – Practically

Makes sense. Thanks Sailx. I’ll prototype it and let you know how it goes. I see one problem. I am not sure what the unit depth is. Without that there’s no way to know the unit of height right? – Autograft