DFA construction in Knuth-Morris-Pratt algorithm

Question

I am referring to the outline of the Knuth-Morris-Pratt (KMP) algorithm for substring search in Sedgewick's book "Algorithms" (4th ed.).

The KMP algorithm uses a backup in substring search based on a deterministic finite automaton (DFA). I understand how the DFA enters the algorithm, however I don't understand how to construct the DFA, which is done by the following code snippet:

dfa[pat.charAt(0)][0] = 1;
for (int X = 0; j = 1; j< M; j++) {
    for (int c = 0; c < R; c++) {
       dfa[c][j] = dfa[c][X];
    }
    dfa[pat.charAt(j)][j] = j+1;
    X = dfa[pat.charAt(j)][X];
}

where M is the the length of the pattern pat and R the size of the alphabet. The charAt() function returns the integer value of the character at the respective position.

Can someone explain in what way this piece of code constructs a dfa? I am lost in the actual intuitive meaning of the inner for-loop.

Eructate

The dfa is a state table with fail links. See this question:#23261438 – Chadburn

Answer 1

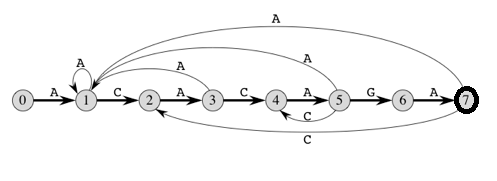
Let us take a look at the following FA for pattern ACACAGA.

The above diagrams represent graphical and tabular representations of pattern ACACAGA.

Here, number of states in DFA is M + 1 where M is length of the pattern. The main thing to construct DFA is to get the next state from the current state for every possible character. Given a character x and a state k, we can get the next state by considering the string “pat[0..k-1]x” which is basically concatenation of pattern characters pat[0], pat1 … pat[k-1] and the character x. The idea is to get length of the longest prefix of the given pattern such that the prefix is also suffix (LPS) of “pat[0..k-1]x”. The value of length gives us the next state.

For example, let us see how to get the next state from current state 5 and character ‘C’ in the above diagram. We need to consider the string, “pat[0..5]C” which is “ACACAC”. The lenght of the longest prefix of the pattern such that the prefix is suffix of “ACACAC”is 4 (“ACAC”). So the next state (from state 5) is 4 for character ‘C’.

// dfa[i][j] = k denotes the transition function will go k'th state 
// with character i from state j

// DFA will go always (i + 1)'th state from i'th state 
//if the character c is equal to current character of pattern 
dfa[pat.charAt(0)][0] = 1;

//  here X is initialized with LPS (longest prefix suffix) 
// of pattern[0....j - 1]. LPS[0] is always 0
for (int X = 0; j = 1; j< M; j++) {
    for (int c = 0; c < R; c++) { // for all possible characters
        // transition function from j'th state taking character c 
        // will go to the same state where it went from X(LPS)'th state
        // taking character c (justify it with an example) 
        dfa[c][j] = dfa[c][X];
    }
    // DFA will go always (i + 1)th state from i'th state if 
    // the character c is equal to current character of pattern
    dfa[pat.charAt(j)][j] = j + 1;
    X = dfa[pat.charAt(j)][X]; // update LPS
}

Nawab

Can someone help me port this to python? pat.charAt(j) returns an error because it's a string. I converted to Unicode using ord() to avoid the error: self.dfa[ord(self.pat[0])][0] = 1 but the algorithm isn't returning a correct answer. Bin: pastebin.com/NyCpfcUK – Sian

X is the LPS for [1..j-1] interval not for [0..j-1] interval. – Repp