Using Scipy curve_fit with piecewise function

Question

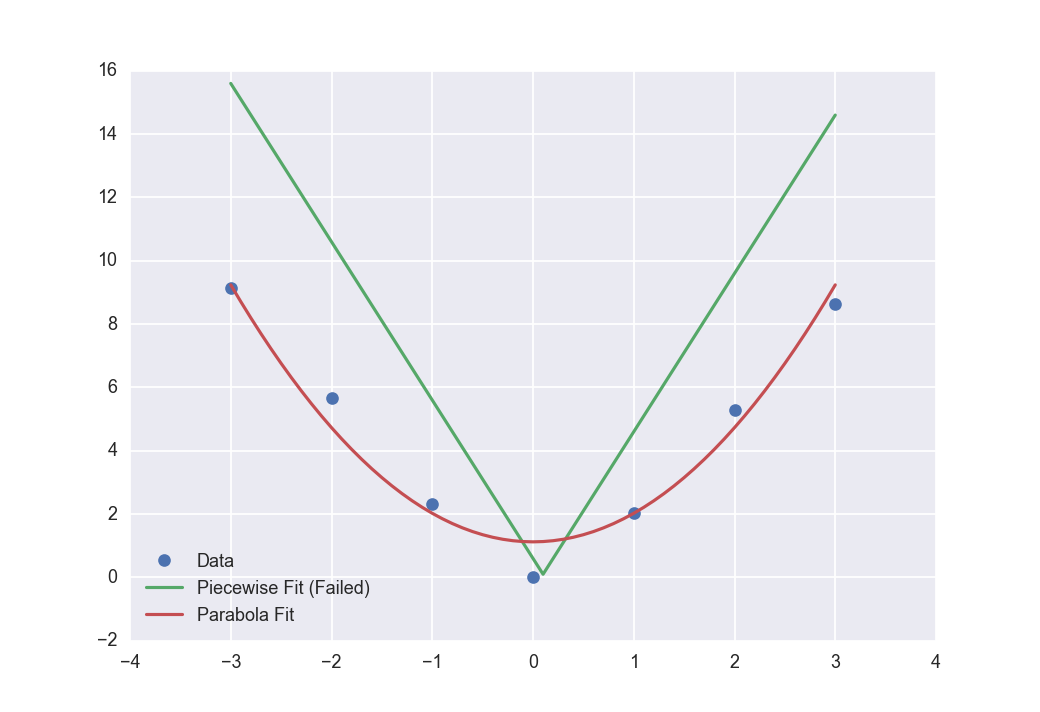
I am getting an optimize warning:

OptimizeWarning: Covariance of the parameters could not be estimated
                 category=OptimizeWarning)

when trying to fit my piecewise function to my data using scipy.optimize.curve_fit. Meaning no fitting is happening. I can easily fit a parabola to my data, and I'm supplying curve_fit with what I feel are good initial parameters. Full code sample below. Does anyone know why curve_fit might not be getting along with np.piecewise? Or am I making a different mistake?

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt


def piecewise_linear(x, x0, y0, k1, k2):
    y = np.piecewise(x, [x < x0, x >= x0],
                     [lambda x:k1*x + y0-k1*x0, lambda x:k2*x + y0-k2*x0])
    return y

def parabola(x, a, b):
    y = a * x**2 + b
    return y

x = np.array([-3, -2, -1, 0, 1, 2, 3])
y = np.array([9.15, 5.68, 2.32, 0.00, 2.05, 5.29, 8.62])


popt_piecewise, pcov = curve_fit(piecewise_linear, x, y, p0=[0.1, 0.1, -5, 5])
popt_parabola, pcov = curve_fit(parabola, x, y, p0=[1, 1])

new_x = np.linspace(x.min(), x.max(), 61)


fig, ax = plt.subplots()

ax.plot(x, y, 'o', ls='')
ax.plot(new_x, piecewise_linear(new_x, *popt_piecewise))
ax.plot(new_x, parabola(new_x, *popt_parabola))

ax.set_xlim(-4, 4)
ax.set_ylim(-2, 16)

Soricine

Answer 1

It is a problem with types, you have to change the following line, so that the x is given as floats:

x = np.array([-3, -2, -1, 0, 1, 2, 3]).astype(np.float)

otherwise the piecewise_linear will might end up casting the types.

Just to be on the safe side you could also make the initial points float here:

popt_piecewise, pcov = curve_fit(piecewise_linear, x, y, p0=[0.1, 0.1, -5., 5.])

Covetous

How ever did you conclude that? – Pertussis

I tried to evaluate the piecewise_linear with the given data points, and it didn't work, so I concluded the problem must be there somewhere. I think it has to do with some strange behaviour of np.piecewise. – Covetous

I tried something the same and entirely missed that. Very good! – Pertussis

I'd suggest x = np.array([-3, -2, -1, 0, 1, 2, 3], dtype=np.float) which immediately tells NumPy to construct an array of floats, instead of constructing an array of integers and then converting the type. – Hardigg

@zaq yes, that is nicer. – Covetous

You could also append a dot in one of the numbers like x = np.array([-3., -2, -1, 0, 1, 2, 3]), that would trigger np to convert it to float. – Covetous

Answer 2

For completeness, I'll point out that fitting a piecewise linear function does not require np.piecewise: any such function can be constructed out of absolute values, using a multiple of np.abs(x-x0) for each bend. The following produces a good fit to the data:

def pl(x, x0, a, b, c):
    y = a*np.abs(x-x0) + b*x + c
    return y

popt_pl, pcov = curve_fit(pl, x, y, p0=[0, 0, 0, 0])

print(pl(x, *popt_pl))

Output is close to original y-values:

[ 8.90899998  5.828       2.74700002 -0.33399996  2.03499998  5.32
  8.60500002]

Hardigg

Answer 3

Similarly to @user6655984, one can use the max() function in this case:

def pl(x, a,b,c,d):
    # piecewise linear using maximum
    return np.maximum(a*x + b, c*x + d)

# OP data
x = np.array([-3, -2, -1, 0, 1, 2, 3])
y = np.array([9.15, 5.68, 2.32, 0.00, 2.05, 5.29, 8.62])

# scipy curve_fit
p = curve_fit(pl, x, y, method='lm', full_output=True)

# plot
new_x = np.linspace(-4,4,100)
fig, ax = plt.subplots()
ax.plot(x, y, 'o', ls='')
ax.plot(new_x, pl(new_x, *p[0]))
ax.set_xlim(-4, 4)
ax.set_ylim(-2, 16)

# ouput
pl(range(-3,4), *p[0])

which will result in the following plot and output:

The max() or min() functions can be used to approximate the outer or inner intersection of curves, respectively, not just for piecewise linear.

Percival