Nonparametric quantile regression curves to scatterplot

Question

I created a scatterplot (multiple groups GRP) with IV=time, DV=concentration. I wanted to add the quantile regression curves (0.025,0.05,0.5,0.95,0.975) to my plot.

And by the way, this is what I did to create the scatter-plot:

attach(E)  ## E is the name I gave to my data
## Change Group to factor so that may work with levels in the legend
Group<-as.character(Group)
Group<-as.factor(Group)

## Make the colored scatter-plot
mycolors = c('red','orange','green','cornflowerblue')
plot(Time,Concentration,main="Template",xlab="Time",ylab="Concentration",pch=18,col=mycolors[Group])

## This also works identically
## with(E,plot(Time,Concentration,col=mycolors[Group],main="Template",xlab="Time",ylab="Concentration",pch=18))

## Use identify to identify each point by group number (to check)
## identify(Time,Concentration,col=mycolors[Group],labels=Group)
## Press Esc or press Stop to stop identify function

## Create legend
## Use locator(n=1,type="o") to find the point to align top left of legend box
legend('topright',legend=levels(Group),col=mycolors,pch=18,title='Group')

Because the data that I created here is a small subset of my larger data, it may look like it can be approximated as a rectangular hyperbole. But I don't want to call a mathematical relationship between my independent and dependent variables yet.

I think nlrq from the package quantreg may be the answer, but I don't understand how to use the function when I don't know the relationship between my variables.

I find this graph from a science article, and I want to do precisely the same kind of graph:

Again, thanks for your help!

Update

Test.csv I was pointed out that my sample data is not reproducible. Here is a sample of my data.

library(evd)
qcbvnonpar(p=c(0.025,0.05,0.5,0.95,0.975),cbind(TAD,DV),epmar=T,plot=F,add=T)

I also tried qcbvnonpar::evd,but the curve doesn't seem very smooth.

Bedpan

If you are unable to provide your own data, try creating a dataset of random numbers and demonstrate your problem. Show us what you've tried. It gives us something to work with as well as being a sign of good faith. – Cryptonym

Oh. I'm sorry--I will make some numbers up. It may be rather large. – Bedpan

This may help you in generating data. #5963769 – Unpile

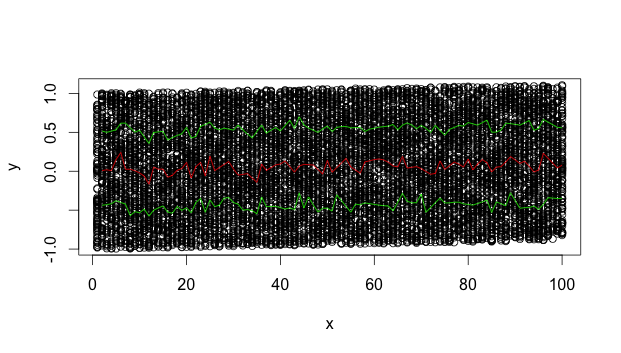
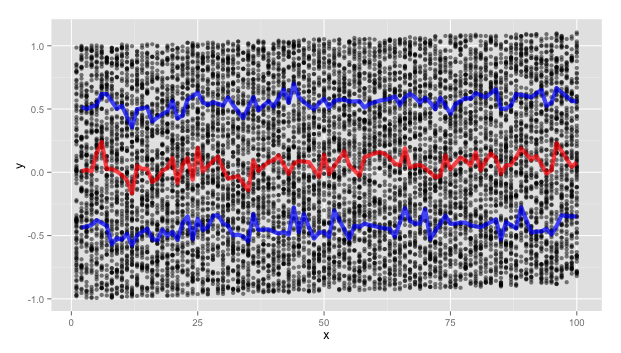
A couple of comments: the figure you show appears to be from works.bepress.com/phil_reiss/16 ? That paper appears to have an associated R package (haven't looked at it ...) It's going to be rather hard (I think) to get completely nonparametric, smooth quantiles. Two possible solutions are (1) fit generalized additive models (e.g. library(splines); rq(y~s(x,5),tau=0.9)); (2) use running estimates of the quantiles. – Selfimmolating

How big is your data set? – Selfimmolating

maybe rqss() from quantreg may also suit you? – Enthymeme

@Roman Luštrik: I will save this page for future reference. It seems my question isn't reproducible with a smaller dataset, and I think I saw someone post a dropbox link to a large file, and I may do the same in the future – Bedpan

@BenBolker: Oh, I should have cited: link. I thought I replied yesterday but the comment didn't show up, my n=1000 approximately – Bedpan

Answer 1

I have in the past frequently struggled with rqss and my issues have almost always been related to the ordering of the points.

You have multiple measurements at various time points, which is why you're getting different lengths. This works for me:

dat <- read.csv("~/Downloads/Test.csv")

library(quantreg)
dat <- plyr::arrange(dat,Time)
fit<-rqss(Concentration~qss(Time,constraint="N"),tau=0.5,data = dat)
with(dat,plot(Time,Concentration))
lines(unique(dat$Time)[-1],fit$coef[1] + fit$coef[-1])

Sorting the data frame prior to fitting the model appears necessary.

Conversational

This works! Thank you so much. I didn't know that ordering could be an issue. – Bedpan

Answer 2

Maybe have a look at quantreg:::rqss for smoothing splines and quantile regression. Sorry for the not so nice example data:

set.seed(1234)
period <- 100
x <- 1:100
y <- sin(2*pi*x/period) + runif(length(x),-1,1)


require(quantreg)
mod <- rqss(y ~ qss(x))
mod2 <- rqss(y ~ qss(x), tau=0.75)
mod3 <- rqss(y ~ qss(x), tau=0.25)
plot(x, y)
lines(x[-1], mod$coef[1] + mod$coef[-1], col = 'red')
lines(x[-1], mod2$coef[1] + mod2$coef[-1], col = 'green')
lines(x[-1], mod3$coef[1] + mod3$coef[-1], col = 'green')

Enthymeme

+1 for rqss() - if non-parametric is what is required and the example image suggests it is a spline-based fit then rqss() is certainly the first place I would look. – Heaviside

It works so beautifully with your example, but I am not sure why, I keep getting Error in xy.coords(x, y) : 'x' and 'y' lengths differ warning for my dataset even though I check that my x and y have the same n. Still working on error debugging :P – Bedpan

Can you give use a little more of your data? Your example data from above is obviously not appropriate. – Enthymeme

Answer 3

In case you want ggplot2 graphic...

I based this example on that of @EDi. I increased the x and y so that the quantile lines would be less wiggly. Because of this increase, I need to use unique(x) in place of x in some of the calls.

Here's the modified set-up:

set.seed(1234)
period <- 100
x <- rep(1:100,each=100)
y <- 1*sin(2*pi*x/period) + runif(length(x),-1,1)


require(quantreg)
mod <- rqss(y ~ qss(x))
mod2 <- rqss(y ~ qss(x), tau=0.75)
mod3 <- rqss(y ~ qss(x), tau=0.25)

Here are the two plots:

# @EDi's base graphics example
plot(x, y)
lines(unique(x)[-1], mod$coef[1] + mod$coef[-1], col = 'red')
lines(unique(x)[-1], mod2$coef[1] + mod2$coef[-1], col = 'green')
lines(unique(x)[-1], mod3$coef[1] + mod3$coef[-1], col = 'green')

# @swihart's ggplot2 example:
## get into dataset so that ggplot2 can have some fun:
qrdf <- data.table(x       = unique(x)[-1],
                   median =  mod$coef[1] +  mod$coef[-1],
                   qupp   = mod2$coef[1] + mod2$coef[-1],
                   qlow   = mod3$coef[1] + mod3$coef[-1]
)

line_size = 2
ggplot() +
  geom_point(aes(x=x, y=y),
             color="black", alpha=0.5) +
  ## quantiles:
  geom_line(data=qrdf,aes(x=x, y=median),
            color="red", alpha=0.7, size=line_size) +
  geom_line(data=qrdf,aes(x=x, y=qupp),
            color="blue", alpha=0.7, size=line_size, lty=1) +
  geom_line(data=qrdf,aes(x=x, y=qlow),
            color="blue", alpha=0.7, size=line_size, lty=1) 

Totaquine