How to do linear regression, taking errorbars into account?

Question

I am doing a computer simulation for some physical system of finite size, and after this I am doing extrapolation to the infinity (Thermodynamic limit). Some theory says that data should scale linearly with system size, so I am doing linear regression.

The data I have is noisy, but for each data point I can estimate errorbars. So, for example data points looks like:

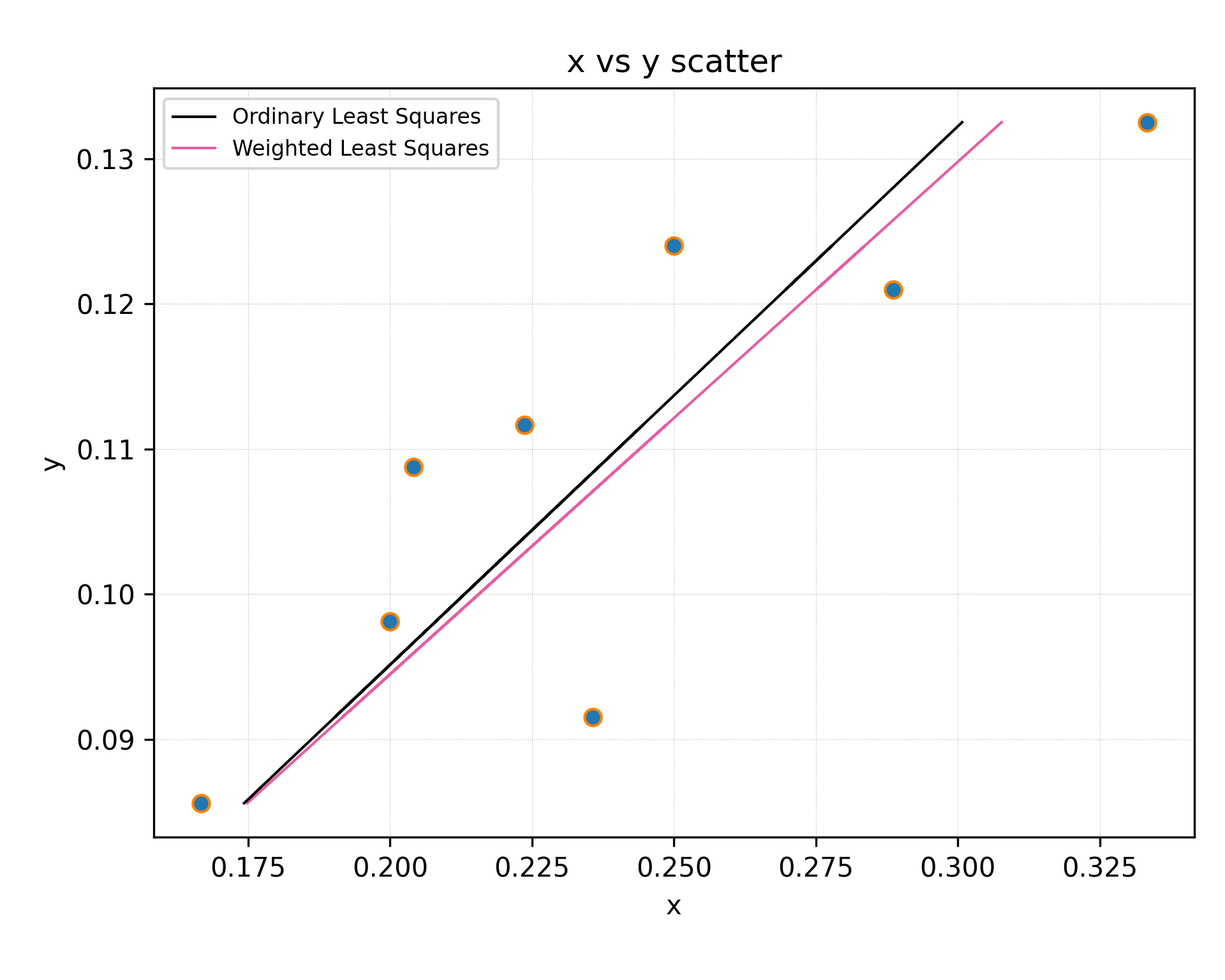
x_list = [0.3333333333333333, 0.2886751345948129, 0.25, 0.23570226039551587, 0.22360679774997896, 0.20412414523193154, 0.2, 0.16666666666666666]
y_list = [0.13250359351851854, 0.12098339583333334, 0.12398501145833334, 0.09152715, 0.11167239583333334, 0.10876248333333333, 0.09814170444444444, 0.08560799305555555]
y_err = [0.003306749165349316, 0.003818446389148108, 0.0056036878203831785, 0.0036635292592592595, 0.0037034897788415424, 0.007576672222222223, 0.002981084130692832, 0.0034913019065973983]

Let's say I am trying to do this in Python.

1. First way that I know is:

   m, c, r_value, p_value, std_err = scipy.stats.linregress(x_list, y_list)
   

   I understand this gives me errorbars of the result, but this does not take into account errorbars of the initial data.

2. Second way that I know is:

   m, c = numpy.polynomial.polynomial.polyfit(x_list, y_list, 1, w = [1.0 / ty for ty in y_err], full=False)
   

Here we use the inverse of the errorbar for the each point as a weight that is used in the least square approximation. So if a point is not really that reliable it will not influence result a lot, which is reasonable.

But I can not figure out how to get something that combines both these methods.

What I really want is what second method does, meaning use regression when every point influences the result with different weight. But at the same time I want to know how accurate my result is, meaning, I want to know what are errorbars of the resulting coefficients.

How can I do this?

Turnedon

Am I misunderstanding you, or are you trying to use the y_err series as weight matrix? – Homoio

Answer 1

Not entirely sure if this is what you mean, but…using pandas, statsmodels, and patsy, we can compare an ordinary least-squares fit and a weighted least-squares fit which uses the inverse of the noise you provided as a weight matrix (statsmodels will complain about sample sizes < 20, by the way).

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['figure.dpi'] = 300

import statsmodels.formula.api as sm

x_list = [0.3333333333333333, 0.2886751345948129, 0.25, 0.23570226039551587, 0.22360679774997896, 0.20412414523193154, 0.2, 0.16666666666666666]
y_list = [0.13250359351851854, 0.12098339583333334, 0.12398501145833334, 0.09152715, 0.11167239583333334, 0.10876248333333333, 0.09814170444444444, 0.08560799305555555]
y_err = [0.003306749165349316, 0.003818446389148108, 0.0056036878203831785, 0.0036635292592592595, 0.0037034897788415424, 0.007576672222222223, 0.002981084130692832, 0.0034913019065973983]

# put x and y into a pandas DataFrame, and the weights into a Series
ws = pd.DataFrame({
    'x': x_list,
    'y': y_list
})
weights = pd.Series(y_err)

wls_fit = sm.wls('x ~ y', data=ws, weights=1 / weights).fit()
ols_fit = sm.ols('x ~ y', data=ws).fit()

# show the fit summary by calling wls_fit.summary()
# wls fit r-squared is 0.754
# ols fit r-squared is 0.701

# let's plot our data
plt.clf()
fig = plt.figure()
ax = fig.add_subplot(111, facecolor='w')
ws.plot(
    kind='scatter',
    x='x',
    y='y',
    style='o',
    alpha=1.,
    ax=ax,
    title='x vs y scatter',
    edgecolor='#ff8300',
    s=40
)

# weighted prediction
wp, = ax.plot(
    wls_fit.predict(),
    ws['y'],
    color='#e55ea2',
    lw=1.,
    alpha=1.0,
)
# unweighted prediction
op, = ax.plot(  
    ols_fit.predict(),
    ws['y'],
    color='k',
    ls='solid',
    lw=1,
    alpha=1.0,
)
leg = plt.legend(
    (op, wp),
    ('Ordinary Least Squares', 'Weighted Least Squares'),
    loc='upper left',
    fontsize=8)

plt.tight_layout()
fig.set_size_inches(6.40, 5.12)
plt.show()

WLS residuals:

[0.025624005084707302,
 0.013611438189866154,
 -0.033569595462217161,
 0.044110895217014695,
 -0.025071632845910546,
 -0.036308252199571928,
 -0.010335514810672464,
 -0.0081511479431851663]

The mean squared error of the residuals for the weighted fit (wls_fit.mse_resid or wls_fit.scale) is 0.22964802498892287, and the r-squared value of the fit is 0.754.

You can obtain a wealth of data about the fits by calling their summary() method, and/or doing dir(wls_fit), if you need a list of every available property and method.

Homoio

Are you sure that the parameter weights should be set to 1/y_err? The example on the statsmodel page uses weights=1/(w**2). They write: "In this example, w is the standard deviation of the error. WLS requires that the weights are proportional to the inverse of the error variance." statsmodels.org/stable/examples/notebooks/generated/wls.html – Bola

@Bola I am not sure! I can’t say for sure whether statsmodels even advised about error variance in WLS 7 years ago so I just used what I’d learned in intro stats to specify the model. Have you tried running the example with weights = 1 / (w ** 2)? Very happy to correct the answer either way. – Homoio

I haven't tried running it with 1/(w**2) weight. I think it should be pretty similar. And I am not sure if 1(w**2) is correct. I think at one point in the past i had decided to use 1/(w**2) for my analysis but that was a long time ago. – Bola

Answer 2

I wrote a concise function to perform the weighted linear regression of a data set, which is a direct translation of GSL's "gsl_fit_wlinear" function. This is useful if you want to know exactly what your function is doing when it performs the fit

def wlinear_fit (x,y,w) :
    """
    Fit (x,y,w) to a linear function, using exact formulae for weighted linear
    regression. This code was translated from the GNU Scientific Library (GSL),
    it is an exact copy of the function gsl_fit_wlinear.
    """
    # compute the weighted means and weighted deviations from the means
    # wm denotes a "weighted mean", wm(f) = (sum_i w_i f_i) / (sum_i w_i)
    W = np.sum(w)
    wm_x = np.average(x,weights=w)
    wm_y = np.average(y,weights=w)
    dx = x-wm_x
    dy = y-wm_y
    wm_dx2 = np.average(dx**2,weights=w)
    wm_dxdy = np.average(dx*dy,weights=w)
    # In terms of y = a + b x
    b = wm_dxdy / wm_dx2
    a = wm_y - wm_x*b
    cov_00 = (1.0/W) * (1.0 + wm_x**2/wm_dx2)
    cov_11 = 1.0 / (W*wm_dx2)
    cov_01 = -wm_x / (W*wm_dx2)
    # Compute chi^2 = \sum w_i (y_i - (a + b * x_i))^2
    chi2 = np.sum (w * (y-(a+b*x))**2)
    return a,b,cov_00,cov_11,cov_01,chi2

To perform your fit, you would do

a,b,cov_00,cov_11,cov_01,chi2 = wlinear_fit(x_list,y_list,1.0/y_err**2)

Which will return the best estimate for the coefficients a (the intercept) and b (the slope) of the linear regression, along with the elements of the covariance matrix cov_00, cov_01 and cov_11. The best estimate on the error on a is then the square root of cov_00 and the one on b is the square root of cov_11. The weighted sum of the residuals is returned in the chi2 variable.

IMPORTANT: this function accepts inverse variances, not the inverse standard deviations as the weights for the data points.

Antimagnetic

Answer 3

sklearn.linear_model.LinearRegression supports specification of weights during fit:

x_data = np.array(x_list).reshape(-1, 1)  # The model expects shape (n_samples, n_features).
y_data = np.array(y_list)
y_err  = np.array(y_err)

model = LinearRegression()
model.fit(x_data, y_data, sample_weight=1/y_err)

Here the sample weight is specified as 1 / y_err. Different versions are possible and often it's a good idea to clip these sample weights to a maximum value in case the y_err varies strongly or has small outliers:

sample_weight = 1 / y_err
sample_weight = np.minimum(sample_weight, MAX_WEIGHT)

where MAX_WEIGHT should be determined from your data (by looking at the y_err or 1 / y_err distributions, e.g. if they have outliers they can be clipped).

Eugene

Answer 4

I found this document helpful in understanding and setting up my own weighted least squares routine (applicable for any programming language).

Typically learning and using optimized routines is the best way to go but there are times where understanding the guts of a routine is important.

Cittern