Using a survival tree from the 'rpart' package in R to predict new observations

Question

I'm attempting to use the "rpart" package in R to build a survival tree, and I'm hoping to use this tree to then make predictions for other observations.

I know there have been a lot of SO questions involving rpart and prediction; however, I have not been able to find any that address a problem that (I think) is specific to using rpart with a "Surv" object.

My particular problem involves interpreting the results of the "predict" function. An example is helpful:

library(rpart)
library(OIsurv)

# Make Data:
set.seed(4)
dat = data.frame(X1 = sample(x = c(1,2,3,4,5), size = 1000, replace=T))
dat$t = rexp(1000, rate=dat$X1)
dat$t = dat$t / max(dat$t)
dat$e = rbinom(n = 1000, size = 1, prob = 1-dat$t )

# Survival Fit:
sfit = survfit(Surv(t, event = e) ~ 1, data=dat)
plot(sfit)

# Tree Fit:
tfit = rpart(formula = Surv(t, event = e) ~ X1 , data = dat, control=rpart.control(minsplit=30, cp=0.01))
plot(tfit); text(tfit)

# Survival Fit, Broken by Node in Tree:
dat$node = as.factor(tfit$where)
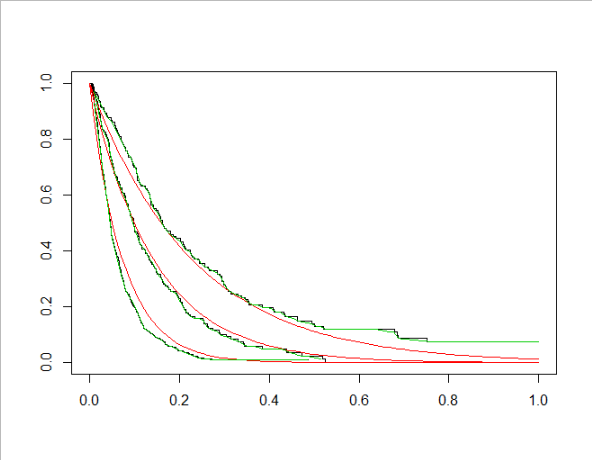
plot( survfit(Surv(dat$t, event = dat$e)~dat$node) )

So far so good. My understanding of what's going on here is that rpart is attempting to fit exponential survival curves to subsets of my data. Based on this understanding, I believe that when I call predict(tfit), I get, for each observation, a number corresponding to the parameter for the exponential curve for that observation. So, for example, if predict(fit)[1] is .46, then this means for the first observation in my original dataset, the curve is given by the equation P(s) = exp(−λt), where λ=.46.

This seems like exactly what I'd want. For each observation (or any new observation), I can get the predicted probability that this observation will be alive/dead for a given time point. (EDIT: I'm realizing this is probably a misconception— these curves don't give the probability of alive/dead, but the probability of surviving an interval. This doesn't change the problem described below, though.)

However, when I try and use the exponential formula...

# Predict:
# an attempt to use the rates extracted from the tree to
# capture the survival curve formula in each tree node.
rates = unique(predict(tfit))
for (rate in rates) {
  grid= seq(0,1,length.out = 100)
  lines(x= grid, y= exp(-rate*(grid)), col=2)
}

What I've done here is split the dataset in the same way the survival tree did, then used survfit to plot a non-parametric curve for each of these partitions. That's the black lines. I've also drawn lines corresponding to the result of plugging in (what I thought was) the 'rate' parameter into (what I thought was) the survival exponential formula.

I understand that the non-parametric and the parametric fit shouldn't necessarily be identical, but this seems more than that: it seems like I need to scale my X variable or something.

Basically, I don't seem to understand the formula that rpart/survival is using under the hood. Can anyone help me get from (1) rpart model to (2) a survival equation for any arbitrary observation?

Resemblance

Answer 1

The survival data are scaled internally exponentially so that the predicted rate in the root node is always fixed to 1.000. The predictions reported by the predict() method are then always relative to the survival in the root node, i.e., higher or lower by a certain factor. See Section 8.4 in vignette("longintro", package = "rpart") for more details. In any case, the Kaplan-Meier curves you are reported correspond exactly to what is also reported in the rpart vignette.

If you want to obtain directly the plots of the Kaplan-Meier curves in the tree and get predicted median survival times, you can coerce the rpart tree to a constparty tree as provided by the partykit package:

library("partykit")
(tfit2 <- as.party(tfit))
## Model formula:
## Surv(t, event = e) ~ X1
## 
## Fitted party:
## [1] root
## |   [2] X1 < 2.5
## |   |   [3] X1 < 1.5: 0.192 (n = 213)
## |   |   [4] X1 >= 1.5: 0.082 (n = 213)
## |   [5] X1 >= 2.5: 0.037 (n = 574)
## 
## Number of inner nodes:    2
## Number of terminal nodes: 3
##
plot(tfit2)

The print output shows the median survival time and the visualization the corresponding Kaplan-Meier curve. Both can also be obtained with the predict() method setting the type argument to "response" and "prob" respectively.

predict(tfit2, type = "response")[1]
##          5 
## 0.03671885 
predict(tfit2, type = "prob")[[1]]
## Call: survfit(formula = y ~ 1, weights = w, subset = w > 0)
## 
##  records    n.max  n.start   events   median  0.95LCL  0.95UCL 
## 574.0000 574.0000 574.0000 542.0000   0.0367   0.0323   0.0408 

As an alternative to the rpart survival trees you might also consider the non-parametric survival trees based on conditional inference in ctree() (using logrank scores) or fully parametric survival trees using the general mob() infrastructure from the partykit package.

Mittel

Thanks for the detailed reply! My goal here, though, is to obtain a P(alive) for any instance at any time point. This seems like it should give me more information than just extracting the median survival time associated with the tree's node for each instance. The only way I've been able to do this is with the predictSurvProb function from the "pec" package, but this function is a little buggy, and I was also hoping it would be more efficient to calculate the survival probabilities from the survival curves themselves, rather than relying on this function. – Resemblance

Yes, and the Kaplan-Meier function is a (non-parametric) estimator of the survivor function S(t), i.e., the probability to still be alive at time t. The Kaplan-Meier function can either be computed by hand using survfit() and the factor based on $where as you did - or via partykit with type = "prob". If you want to fit a parametric model (e.g., exponential or Weibull) in each leaf, you can use survreg() instead of survfit(). – Mittel

Sorry, I'm not completely following: Could you edit your post to provide actual code that would give me S(t) for a given t and a given instance? E.g., given an rpart object tfit and an instance dat[1,], and a time dat[1,'t'], what code should I use to get S(t) for that instance and that t? – Resemblance

I don't understand why you want an edit of my answer. The code snippet predict(tfit2, type = "prob")[[1]] shown above extracts the fitted survfit object for the first observation. From this you can extract all the "usual" quantities you like. For example, look at the summary() of the object which shows you the full Kaplan-Meier curve coordinates with several additional pieces of information. – Mittel

I was hoping for an edit because extracting the probabilities from the summary of the survfit object (as you're instructing) isn't trivial; but I think I should be able to figure it out. – Resemblance

But this is then really a question about survfit and survival for which there are again useful books, tutorials, etc. But I think that if you do: km1 <- predict(tfit2, type = "prob")[[1]] and then summary(km1) you should see everything you need. You can easily get quantiles from this, e.g., quantile(km1, c(0.2, 0.5, 0.8)) which gives you the times at which S(t) is 0.8, 0.5, and 0.2, respectively. Or if you want a function you can do km1f <- approxfun(km1$time, km1$surv) and then km1f(c(0.011, 0.037, 0.094)) etc. – Mittel

Answer 2

@Achim Zeileis's answer is very helpful, but it seems that the exact @jwdink's question was not answered. I understood it as "If RPart tree splits by best exponential survival fit, what are the Lambdas for these fits in absolute terms, so we can use these exponential survival functions to make predictions". The RPart summary does show the estimated rate, but only in relative terms assuming that the entire population has rate of 1. To overcome, one can fit an exponential survreg, take the referenced lambda from there and then multiply RPart predicted rates by that number (see code below).

That said, this is not how survival rates in RPart are predicted out of a tree. I did not find survival prediction function directly in RPart, however as Achim pointed above, partykit uses Kaplan-Meier estimates, i.e. non-parametric survival from those ending up in a respective final leaf. I think it is the same in survival random forest trees, where K-M curves are used in the final leaves.

The simulated data in this question uses exponential distribution, so K-M and exponential survival curves will be similar by design, however for a different simulated or real-life distribution estimated exponential rates by RPart tree and using K-M curves in the final leaves (of the same tree) will give different survival rates.

sfit = survfit(Surv(t, event = e) ~ 1, data=dat)
tfit = rpart(formula = Surv(t, event = e) ~ X1 , data = dat, control=rpart.control(minsplit=30, cp=0.01))
plot(tfit); text(tfit)

# Survival Fit, Broken by Node in Tree:
dat$node = as.factor(tfit$where)
table(dat$node)
s0 = survreg(Surv(t,e)~ 1, data =  dat, dist = "exponential") #-0.6175
e0 = exp(-summary(s0)$coefficients[1]); e0 #1.854
rates = unique(predict(tfit))
#1) plot K-M curves by node (black):
plot( survfit(Surv(dat$t, event = dat$e)~dat$node) )

#2) plot exponential survival with rates = e0 * RPart rates (red):
for (rate in rates) {
  grid= seq(0,1,length.out = 100)
  lines(x= grid, y= exp(-e0*rate*(grid)), col=2)
}
#3) plot partykit survival curves based on RPart tree (green)
library(partykit)
tfit2 <- as.party(tfit)
col_n = 1
for (node in names(table(dat$node))){
  predict_curve = predict(tfit2, newdata = dat[dat$node == node, ], type = "prob")  
  surv_esitmated = approxfun(predict_curve[[1]]$time, predict_curve[[1]]$surv)
  lines(x= grid, y= surv_esitmated(grid), col = 2+col_n)
  col_n=+1
}

Sasin