Fast way to find closest line segment for a large set of planar points [Python]

Question

Problem

Given are n=10000 points and m=1000 line segments in a plane. The task is to determine the closest segment to each point. A fast solution in Python is preferred.

Specifications

Line segments are defined by their endpoints and the distance is Euclidean. Lines can cross. The minimum distance should be calculated to the entire segment, not just the endpoints. The distance to the nearest line segment is unnecessary.

Graphical example

This picture demonstrates how to find the closest line segment for a small number of points and segments. The points are colored based on their nearest line segment.

Possible solution strategy

One possible method to achieve this is by using a Voronoi tessellation of line segments and determining which cell a point lies in (link). However, calculating this tessellation is not easy and would require external packages. Also crossing lines could be a problem. Additionally, I am not concerned with the exact shape of the Voronoi cells. Although I do not want to exclude this method, it appears that there may be a simpler solution by vectorizing the distance calculation.

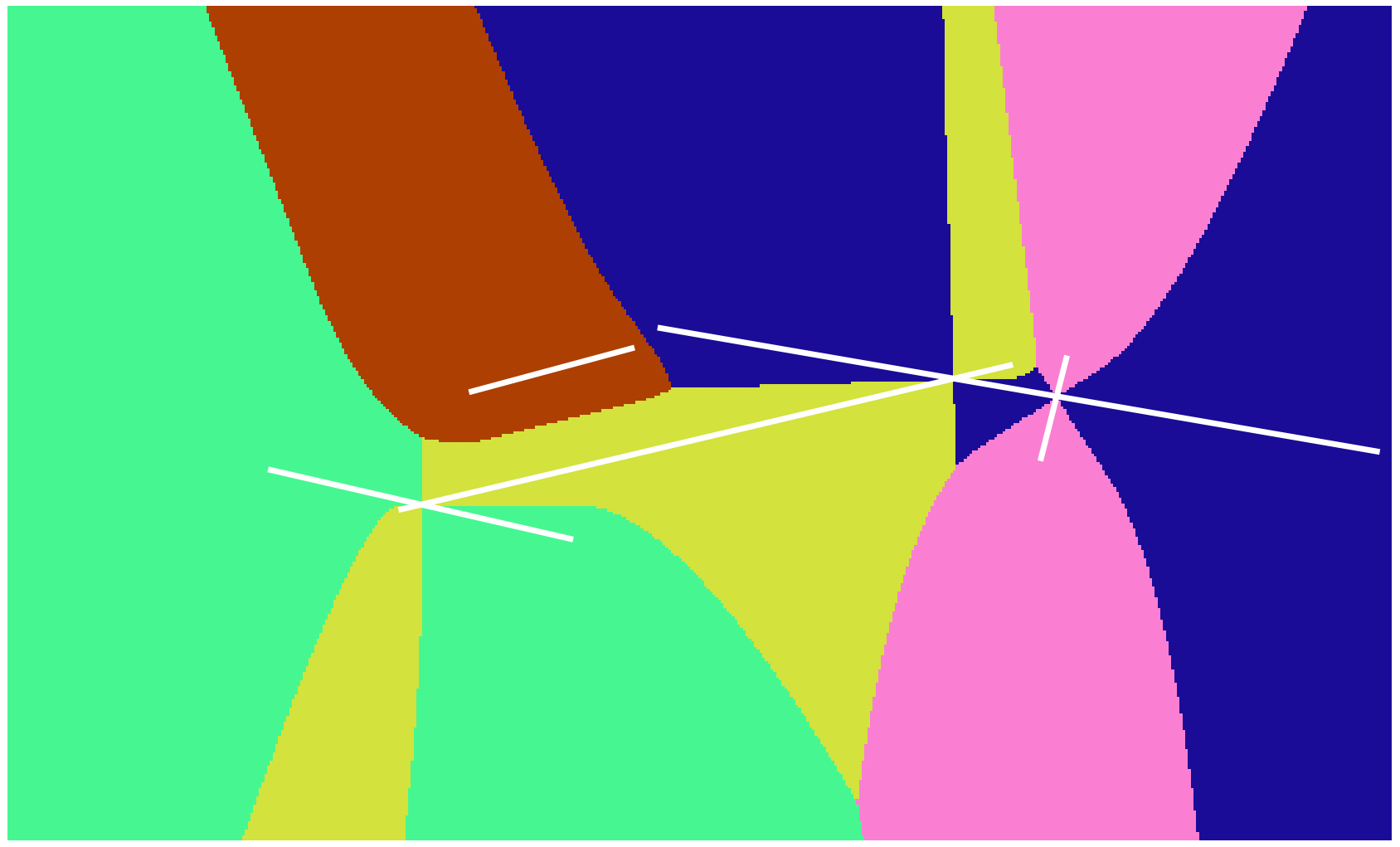
The picture shows the Voronoi tessellation of the previous example. Voronoi cells are colored based on line segment color.

Related question

This problem has already been asked in this post, but here the problem contains many points and segments. Speed is an issue.

Hints for solution

A solution has already been presented that is fast. For the given CPU it takes 0.2s for n=10000,m=1000 and 7.5s for n=100000,m=10000.

Can a substantially faster algorithm be implemented in Python, achieving at least a 30% improvement in speed over the existing solution? More precisely, if the existing solution (function dist_fast) takes time x on an individual CPU, then the improved solution should take at most time 0.7x. For better comparison the case n=10000,m=1000 and the case n=100000,m=10000 can be tested.

Gurgle

Answer 1

Vectorization of one loop can increase speed by 100 times

By modifying the Python algorithm from this post I was able to achieve a speed improvement of a factor of 100 (function dist_fast in the code below). I vectorized over m and calculated repeating steps in advance.

For n=10000 and m=1000, the given CPU takes 20s when the original algorithm is looped over n and m, but only 0.2s when we loop only over m.

---

import numpy as np, time

def dist_fast(p,segment):
  n=p.shape[1]
  segment_closest=np.zeros(n,dtype=int)
  dxs=segment[2,:]-segment[0,:]
  dys=segment[3,:]-segment[1,:]
  q=dxs**2+dys**2;dxsq=dxs/q;dysq=dys/q
  for i in range(n):
    dx=p[0,i]-segment[0];dy=p[1,i]-segment[1]
    u=np.clip(dx*dxsq+dy*dysq,0,1)
    sqdist = (dx-u*dxs)**2+(dy-u*dys)**2
    segment_closest[i]=np.argmin(sqdist)
  return segment_closest

def dist_slow(p,segment):
  
  #use distance function from https://stackoverflow.com/a/2233538
  def dist(x1, y1, x2, y2, x3, y3):
    px = x2-x1
    py = y2-y1
    norm = px*px + py*py
    u =  ((x3 - x1) * px + (y3 - y1) * py) / float(norm)
    if u > 1:
      u = 1
    elif u < 0:
      u = 0
    x = x1 + u * px
    y = y1 + u * py
    dx = x - x3
    dy = y - y3
    sqdist = dx*dx + dy*dy
    return sqdist
  
  n=p.shape[1];m=segment.shape[1]
  segment_closest=np.zeros(n,dtype=int)
  d=np.zeros(m)
  for i in range(n):
    x3,y3=p[0,i],p[1,i]
    for j in range(m):
      x1,y1,x2,y2=segment[0,j],segment[1,j],segment[2,j],segment[3,j]
      d[j]=dist(x1,y1,x2,y2,x3,y3)
    segment_closest[i]=np.argmin(d)
  return segment_closest      
      
n=10**4 #number of points  
m=10**3 #number of line segments

#define repeatable random numbers
np.random.seed(0) 
#create random points and line segments for testing
p=np.random.rand(2,n) #x,y of points
segment=np.random.rand(4,m) #x1,y1,x2,y2  start and end of line segments


#fast algorithm, vectorized, 1 loop
t1=time.time()  
segment_closest1=dist_fast(p,segment)
time_fast=time.time()-t1

#slow algorithm, 2 loops
t1=time.time()  
segment_closest2=dist_slow(p,segment)
time_slow=time.time()-t1

print('Time vectorized algorithm: ',time_fast)
print('Time non-vectorized algorithm: ',time_slow)
print('Results are equal?',np.array_equal(segment_closest1,segment_closest2))

Gurgle

Answer 2

A quick modification of your code using numba.

pip install numba==0.58.1

import numpy as np, time

#<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
from numba import jit

@jit
def jit_dist_fast(p,segment):
  n=p.shape[1]
  segment_closest=np.zeros(n,dtype=int)
  dxs=segment[2,:]-segment[0,:]
  dys=segment[3,:]-segment[1,:]
  q=dxs**2+dys**2;dxsq=dxs/q;dysq=dys/q
  for i in range(n):
    dx=p[0,i]-segment[0];dy=p[1,i]-segment[1]
    u=np.clip(dx*dxsq+dy*dysq,0,1)
    sqdist = (dx-u*dxs)**2+(dy-u*dys)**2
    segment_closest[i]=np.argmin(sqdist)
  return segment_closest
#>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

def dist_fast(p,segment):
  n=p.shape[1]
  segment_closest=np.zeros(n,dtype=int)
  dxs=segment[2,:]-segment[0,:]
  dys=segment[3,:]-segment[1,:]
  q=dxs**2+dys**2;dxsq=dxs/q;dysq=dys/q
  for i in range(n):
    dx=p[0,i]-segment[0];dy=p[1,i]-segment[1]
    u=np.clip(dx*dxsq+dy*dysq,0,1)
    sqdist = (dx-u*dxs)**2+(dy-u*dys)**2
    segment_closest[i]=np.argmin(sqdist)
  return segment_closest

def dist_slow(p,segment):
  
  #use distance function from https://stackoverflow.com/a/2233538
  def dist(x1, y1, x2, y2, x3, y3):
    px = x2-x1
    py = y2-y1
    norm = px*px + py*py
    u =  ((x3 - x1) * px + (y3 - y1) * py) / float(norm)
    if u > 1:
      u = 1
    elif u < 0:
      u = 0
    x = x1 + u * px
    y = y1 + u * py
    dx = x - x3
    dy = y - y3
    sqdist = dx*dx + dy*dy
    return sqdist
  
  n=p.shape[1];m=segment.shape[1]
  segment_closest=np.zeros(n,dtype=int)
  d=np.zeros(m)
  for i in range(n):
    x3,y3=p[0,i],p[1,i]
    for j in range(m):
      x1,y1,x2,y2=segment[0,j],segment[1,j],segment[2,j],segment[3,j]
      d[j]=dist(x1,y1,x2,y2,x3,y3)
    segment_closest[i]=np.argmin(d)
  return segment_closest      
      
n=10**4 #number of points  
m=10**3 #number of line segments

#define repeatable random numbers
np.random.seed(0) 
#create random points and line segments for testing
p=np.random.rand(2,n) #x,y of points
segment=np.random.rand(4,m) #x1,y1,x2,y2  start and end of line segments


#fast algorithm, vectorized, 1 loop
t1=time.time()  
segment_closest1=dist_fast(p,segment)
time_fast=time.time()-t1


#slow algorithm, 2 loops
t1=time.time()  
segment_closest2=dist_slow(p,segment)
time_slow=time.time()-t1
#>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
# jitted algorithm
t1=time.time()  
segment_closest3=jit_dist_fast(p,segment)
time_jitted_first_run=time.time()-t1

t1=time.time()  
segment_closest3=jit_dist_fast(p,segment)
time_faster=time.time()-t1
#>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
print('Time vectorized algorithm: ',time_fast)
print('Time non-vectorized algorithm: ',time_slow)

#<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
print('Time first run of jitted vectorized algorithm: ',time_jitted_first_run)
print('Time jitted vectorized algorithm: ',time_faster)
#>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
print('Results are equal?',np.array_equal(segment_closest1,segment_closest2))
print('Results are equal?',np.array_equal(segment_closest1,segment_closest3))

Using jit basically compiles the python like c, so the first run will cause some overhead. Later runs will be faster (because compiled). I find around 75% improvement over the original. If your intention is to run this algorithm many times, then using jit definitely gains.

output:

Time vectorized algorithm:  0.2614469528198242
Time non-vectorized algorithm:  17.305463314056396
Time first run of jitted vectorized algorithm:  2.0804057121276855
Time jitted vectorized algorithm:  0.048833370208740234
Results are equal? True
Results are equal? True

Another way is to use something like cffi or cpython to compile your code into lib based on generated c code and then call the lib. There is a way to avoid the compiling during run time. See here.

Gurgle

Don't mix cpython and cython up ;) – Twelfthtide