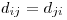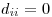Using Numpy to find the average distance in a set of points

Question

I have an array of points in unknown dimensional space, such as:

data=numpy.array(
[[ 115, 241, 314],
[ 153, 413, 144],
[ 535, 2986, 41445]])

and I would like to find the average euclidean distance between all points.

Please note that I have over 20,000 points, so I would like to do this as efficiently as possible.

Thanks.

Phosphorite

When you say "all points" do you mean the distance from point 1 to point 2, point 1 to point 3, ... point 1 to point N, the distance from point 2 to point 3, ... point 2 to point N, ... point N-1 to point N? – Buckboard

I recommend that you tag this as an algorithm question. You are really trying to find an algorithm that can do better than the naive O(dn^2), where d is the dimensionality and n is the number of such points. This can be trivially parallelized into n operations, each with runtime O(nd), that can be merged in O(n) time, but given that you aren't going to have 20,000 processors, it seems like you are looking for a more efficient algorithm.... so maybe someone can give a good adversary argument as to why it is Omega(dn^2), or someone can come up with a clever way to do it faster... – Plexor

Efficiency does not always mean it will be fast enough :) I think this is O(N*N) so you will need to calculate 200 million distances! – Winy

Do you need all of the distances, or just the distances that satisfy some requirement? – Hackler

The larger project is finding the outlier points. The method I am using requires the average distance. – Phosphorite

If you just need to find outliers, why not find the point that is the average of the distribution (average x, average y, average z) and use the std deviation of the distance away from this point to determine outliers. That will be an O(N) algorithm rather than this O(N^2) algorithm you are using. – Interferon

@Justin, you beat me to my post. – Plexor

If your data is somewhat normally distributed in R space, Grubbs' test might be a good option. It only requires you to compute the mean point and the standard deviation. en.wikipedia.org/wiki/Grubbs'_test_for_outliers – Pascasia

Answer 1

Well, I don't think that there is a super fast way to do this, but this should do it:

tot = 0.

for i in xrange(data.shape[0]-1):
    tot += ((((data[i+1:]-data[i])**2).sum(1))**.5).sum()

avg = tot/((data.shape[0]-1)*(data.shape[0])/2.)

Interferon

This takes ~35 seconds to run on a 1.86 GHz Win32 machine. If that's ok for your application, I'd say go with it. @Justin - a couple of small bugs: you should have tot += (...).mean(), and avg = tot/(data.shape[0]-1). – Buckboard

@Buckboard I agree that there was a bug - I was dividing the total by the wrong number, but now I've fixed it. – Interferon

Answer 2

If you have access to scipy, you could try the following:

scipy.spatial.distance.cdist(data,data)

Cockiness

I think OP actually wants scipy.spatial.distance.pdist – Bakst

Answer 3

There's no getting around the number of evaluations:

Sum[n-i, {i, 0, n}] = http://www.equationsheet.com/latexrender/pictures/27744c0bd81116aa31c138ab38a2aa87.gif

But you can save yourself the expense of all those square roots if you can get by with an approximate result. It depends on your needs.

If you're going to calculate an average, I would advise you to not try putting all the values into an array before calculating. Just calculate the sum (and sum of squares if you need standard deviation as well) and throw away each value as you calculate it.

Since and , I don't know if this means you have to multiply by two somewhere.

Anacreontic

Answer 4

Now that you've stated your goal of finding the outliers, you are probably better off computing the sample mean and, with that, the sample variance, since both those operations will give you an O(nd) operation. With that, you should be able to find outliers (e.g. excluding points further from the mean than some fraction of the std. dev.), and that filtering process should be possible to perform in O(nd) time for a total of O(nd).

You might be interested in a refresher on Chebyshev's inequality.

Plexor

Answer 5

Is it ever worthwhile to optimize without a working solution? Also, computation of a distance matrix over the entire data set rarely needs to be fast because you only do it once--when you need to know a distance between two points, you just look it up, it's already calculated.

So if you don't have a place to start, here's one. If you want to do this in Numpy without the need to write any inline fortran or C, that should be no problem, though perhaps you want to include this small vector-based virtual machine called "numexpr" (available on PyPI, trivial to intall) which in this case gave a 5x performance boost versus Numpy alone.

Below i've calculated a distance matrix for 10,000 points in 2D space (a 10K x 10k matrix giving the distance between all 10k points). This took 59 seconds on my MBP.

import numpy as NP
import numexpr as NE

# data are points in 2D space (x, y)--obviously, this code can accept data of any dimension
x = NP.random.randint(0, 10, 10000)
y = NP.random.randint(0, 10, 10000)
fnx = lambda q : q - NP.reshape(q, (len(q), 1))
delX = fnx(x)
delY = fnx(y)
dist_mat = NE.evaluate("(delX**2 + delY**2)**0.5")

Dear

Answer 6

If you want a fast and inexact solution, you could probably adapt the Fast Multipole Method algorithm.

Points that are separated by a small distance have a smaller contribution to the final average distance, so it would make sense to group points into clusters and compare the clusters distances.

Kath

Answer 7

in just a set of points on a horizontal axis (1D), the "euclidean distance" is simply the difference between points, and you can use np.diff to calculate their mean very easily:

import numpy as np

arr = np.array([10,80,50,5,25,4])
avg = np.mean (    abs ( np.diff(arr)  )     )
print(avg)

which prints: 37.2

you can exclude abs if you want to consider negative differences in the resulted mean. good luck.

Mcdougal