How to calculate the midpoint of several geolocations in python

Question

Is there's a library or a way to calculate the center point for several geolocations points? This is my list of geolocations based in New York and want to find the approximate midpoint geolocation

L = [
     (-74.2813611,40.8752222),
     (-73.4134167,40.7287778),
     (-74.3145014,40.9475244),
     (-74.2445833,40.6174444),
     (-74.4148889,40.7993333),
     (-73.7789256,40.6397511)
    ]

Lodger

Check out this question on the GIS stack exchange: gis.stackexchange.com/questions/12120/… – Potentilla

how about calculating the simple average of all coordinates (they are quite close to each other)? – Precinct

@Potentilla that is a very helpful source! thank you! – Lodger

@Precinct yes, they are close. I will calculate the averages for lat and long as center point. thank you! – Lodger

Answer 1

After the comments I received and comment from HERE

With coordinates that close to each other, you can treat the Earth as being locally flat and simply find the centroid as though they were planar coordinates. Then you would simply take the average of the latitudes and the average of the longitudes to find the latitude and longitude of the centroid.

lat = []
long = []
for l in L :
  lat.append(l[0])
  long.append(l[1])

sum(lat)/len(lat)
sum(long)/len(long)

-74.07461283333332, 40.76800886666667

Lodger

Answer 2

Based on: https://gist.github.com/tlhunter/0ea604b77775b3e7d7d25ea0f70a23eb

Assume you have a pandas DataFrame with latitude and longitude columns, the next code will return a dictionary with the mean coordinates.

import math

x = 0.0
y = 0.0
z = 0.0

for i, coord in coords_df.iterrows():
    latitude = math.radians(coord.latitude)
    longitude = math.radians(coord.longitude)

    x += math.cos(latitude) * math.cos(longitude)
    y += math.cos(latitude) * math.sin(longitude)
    z += math.sin(latitude)

total = len(coords_df)

x = x / total
y = y / total
z = z / total

central_longitude = math.atan2(y, x)
central_square_root = math.sqrt(x * x + y * y)
central_latitude = math.atan2(z, central_square_root)

mean_location = {
    'latitude': math.degrees(central_latitude),
    'longitude': math.degrees(central_longitude)
    }

Fitzger

Answer 3

Considering that you are using signed degrees format (more), simple averaging of latitude and longitudes would create problems for even small regions near to antimeridian (i.e. + or - 180-degree longitude) due to discontinuity of longitude value at this line (sudden jump between -180 to 180).

Consider two locations whose longitudes are -179 and 179, their mean would be 0, which is wrong.

Smilacaceous

Answer 4

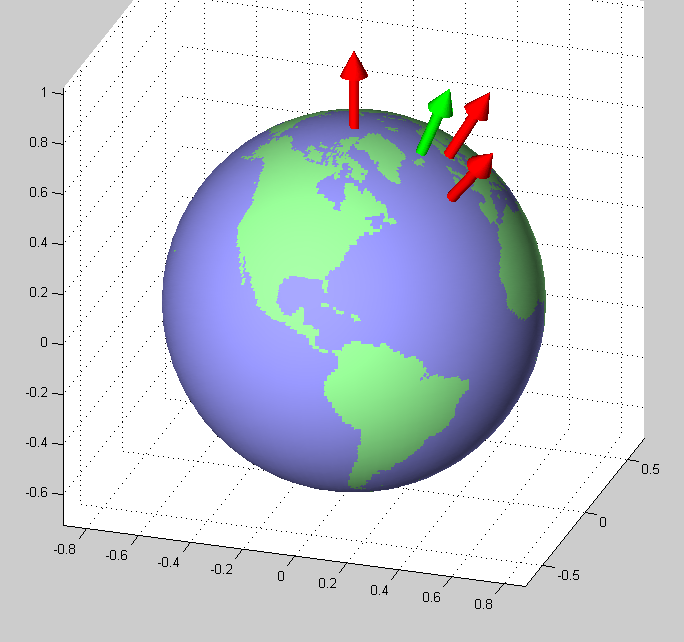
This link can be useful, first convert lat/lon into an n-vector, then find average. A first stab at converting the code into Python is below

import numpy as np
import numpy.linalg as lin

E = np.array([[0, 0, 1],
              [0, 1, 0],
              [-1, 0, 0]])

def lat_long2n_E(latitude,longitude):
    res = [np.sin(np.deg2rad(latitude)),
           np.sin(np.deg2rad(longitude)) * np.cos(np.deg2rad(latitude)),
           -np.cos(np.deg2rad(longitude)) * np.cos(np.deg2rad(latitude))]
    return np.dot(E.T,np.array(res))

def n_E2lat_long(n_E):
    n_E = np.dot(E, n_E)
    longitude=np.arctan2(n_E[1],-n_E[2]);
    equatorial_component = np.sqrt(n_E[1]**2 + n_E[2]**2 );
    latitude=np.arctan2(n_E[0],equatorial_component);
    return np.rad2deg(latitude), np.rad2deg(longitude)

def average(coords):
    res = []
    for lat,lon in coords:
        res.append(lat_long2n_E(lat,lon))
    res = np.array(res)
    m = np.mean(res,axis=0)
    m = m / lin.norm(m)
    return n_E2lat_long(m)
        

n = lat_long2n_E(30,20)
print (n)
print (n_E2lat_long(np.array(n)))

# find middle of france and libya
coords = [[30,20],[47,3]]
m = average(coords)
print (m)

Irrespirable

Thank you @BBSysDyn. This is a wonderful explanation! – Lodger

Answer 5

I would like to improve on the @BBSysDyn'S answer. The average calculation can be biased if you are calculating the center of a polygon with extra vertices on one side. Therefore the average function can be replaced with centroid calculation explained here

def get_centroid(points):

    x = points[:,0]
    y = points[:,1]
    
    # Solving for polygon signed area
    A = 0
    for i, value in enumerate(x):
        if i + 1 == len(x):
            A += (x[i]*y[0] - x[0]*y[i])
        else:
            A += (x[i]*y[i+1] - x[i+1]*y[i])
    A = A/2

    #solving x of centroid
    Cx = 0
    for i, value in enumerate(x):
        if i + 1 == len(x):
            Cx += (x[i]+x[0]) * ( (x[i]*y[0]) - (x[0]*y[i]) )
        else:
            Cx += (x[i]+x[i+1]) * ( (x[i]*y[i+1]) - (x[i+1]*y[i]) )
    Cx = Cx/(6*A)

    #solving y of centroid
    Cy = 0
    for i , value in enumerate(y):
        if i+1 == len(x):
            Cy += (y[i]+y[0]) * ( (x[i]*y[0]) - (x[0]*y[i]) )
        else:
            Cy += (y[i]+y[i+1]) * ( (x[i]*y[i+1]) - (x[i+1]*y[i]) )
    Cy = Cy/(6*A)

    return Cx, Cy

Note: If it is a polygon or more than 2 points, they must be listed in order that the polygon or shape would be drawn.

Laundress

Thanks! it works really well :), for vectors with 2 or 3 values A sometimes is equal to 0 so it breaks, I added a flag in my implementation to check that. – Batting

I don’t get it, this is very different from BBSysDyn answer, as this computes the center of a polygon on an Euclidean plane, assuming lat/lon coordinates to be equivalent to Cartesian coordinates, instead of using vectors from the center of earth as a starting point. – Fari