How to improve accuracy of a FeedForward Neural Network?

Question

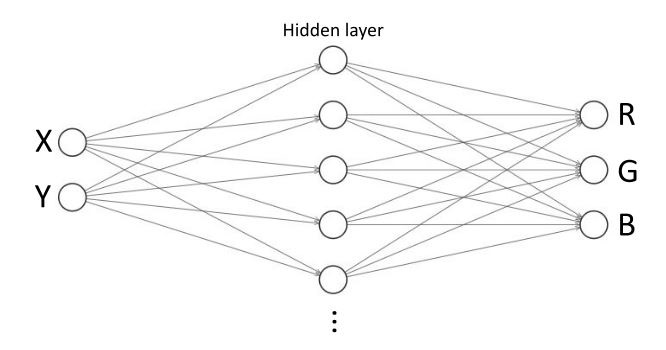
I want to draw StackOverflow's logo with this Neural Network:

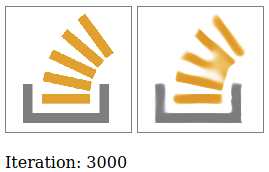
The NN should ideally become [r, g, b] = f([x, y]). In other words, it should return RGB colors for a given pair of coordinates. The FFNN works pretty well for simple shapes like a circle or a box. For example after several thousands epochs a circle looks like this:

Try it yourself: https://codepen.io/adelriosantiago/pen/PoNGeLw

---

However since StackOverflow's logo is far more complex even after several thousands of iterations the FFNN's results are somewhat poor:

From left to right:

1. StackOverflow's logo at 256 colors.
2. With 15 hidden neurons: The left handle never appears.
3. 50 hidden neurons: Pretty poor result in general.
4. 0.03 as learning rate: Shows blue in the results (blue is not in the orignal image)
5. A time-decreasing learning rate: The left handle appears but other details are now lost.

Try it yourself: https://codepen.io/adelriosantiago/pen/xxVEjeJ

Some parameters of interest are synaptic.Architect.Perceptron definition and learningRate value.

---

How can I improve the accuracy of this NN?

Could you improve the snippet? If so, please explain what you did. If there is a better NN architecture to tackle this type of job could you please provide an example?

Additional info:

• Artificial Neural Network library used: Synaptic.js
• To run this example in your localhost: See repository

Auscultate

Answer 1

By adding another layer, you get better results :

let perceptron = new synaptic.Architect.Perceptron(2, 15, 10, 3)

There are small improvements that you can do to improve efficiency (marginally): Here is my optimized code:

const width = 125
const height = 125
const outputCtx = document.getElementById("output").getContext("2d")
const iterationLabel = document.getElementById("iteration")
const stopAtIteration = 3000
let perceptron = new synaptic.Architect.Perceptron(2, 15, 10, 3)
let iteration = 0

let inputData = (() => {
  const tempCtx = document.createElement("canvas").getContext("2d")
  tempCtx.drawImage(document.getElementById("input"), 0, 0)
  return tempCtx.getImageData(0, 0, width, height)
})()

const getRGB = (img, x, y) => {
  var k = (height * y + x) * 4;
  return [
    img.data[k] / 255, // R
    img.data[k + 1] / 255, // G
    img.data[k + 2] / 255, // B
    //img.data[(height * y + x) * 4 + 3], // Alpha not used
  ]
}
const paint = () => {
  var imageData = outputCtx.getImageData(0, 0, width, height)
  for (let x = 0; x < width; x++) {
    for (let y = 0; y < height; y++) {
      var rgb = perceptron.activate([x / width, y / height])
      var k = (height * y + x) * 4;
      imageData.data[k] = rgb[0] * 255
      imageData.data[k + 1] = rgb[1] * 255
      imageData.data[k + 2] = rgb[2] * 255
      imageData.data[k + 3] = 255 // Alpha not used
    }
  }
  outputCtx.putImageData(imageData, 0, 0)

  setTimeout(train, 0)
}

const train = () => {
  iterationLabel.innerHTML = ++iteration

  if (iteration > stopAtIteration) return

  let learningRate = 0.01 / (1 + 0.0005 * iteration) // Attempt with dynamic learning rate
  //let learningRate = 0.01 // Attempt with non-dynamic learning rate
      
  for (let x = 0; x < width; x += 1) {
    for (let y = 0; y < height; y += 1) {
      perceptron.activate([x / width, y / height])
      perceptron.propagate(learningRate, getRGB(inputData, x, y))
    }
  }
  paint()
}

const startTraining = (btn) => {
  btn.disabled = true
  train()
}

EDIT : I made another CodePen with even better results:

https://codepen.io/xurei/pen/KKzWLxg

It is likely to be over-fitted BTW. The perceptron definition:

let perceptron = new synaptic.Architect.Perceptron(2, 8, 15, 7, 3)

Cheep

Another thing you could try is to use something else than RGB. I believe Lab* or HSV color spaces might work better. – Cheep

Also, your error function is currently linear. I have an intuition that Mean Square Error may work better too. – Cheep

Thanks! The result looks pretty good. The bounty time has expired and I decided to award it to you. The only thing that I would really want to know is the reason behind the new values. Basically how does one chooses the right ones? Luck? Thanks! – Auscultate

Thanks for the reward, much appreciated :-) To answer your question : A composition of Luck and experience. Basically, a perceptron with one layer is like a linear clustering algorithm (ie it can define a plane that separate a space). Each extra layer allows the NN to transform the input to another form, that is easier to linearly split. Based on this, my thinking was "the image is too complex to be separated linearly, let's try with extra layers". Check the Kernel trick for more theory : en.wikipedia.org/wiki/Kernel_method. – Cheep

Answer 2

Taking some insights from the lecture/slides of Bhiksha Raj (from slides 62 onwards), and summarizing as below:

Each node can be assumed like a linear classifier, and combination of several nodes in a single layer of neural networks can approximate any basic shapes. For example, a rectangle can be formed by 4 nodes for each lines, assuming each nodes contributes to one line, and the shape can be approximated by the final output layer.

Falling back to the summary of complex shapes such as circle, it may require infinite nodes in a layer. Or this would likely hold true for a single layer with two disjoint shapes (A non-overlapping triangle and rectangle). However, this can still be learnt using more than 1 hidden layers. Where, the 1st layer learns the basic shapes, followed by 2nd layer approximating their disjoint combinations.

Thus, you can assume that this logo is combination of disjoint rectangles (5 rectangles for orange and 3 rectangles for grey). We can use atleast 32 nodes in 1st hidden layer and few nodes in the 2nd hidden layer. However, we don't have control over what each node learns. Hence, a few more number of neurons than required neurons should be helpful.

Adoration