I was reading up algorithms for finding the minimum spanning tree(in case of weighted graphs) and for finding if a graph has a hamiltonian path(which depends on the presence of a hamiltonian cycle). I got everything messed up. So whats the difference between a hamiltonian path and a spanning tree? Both cover all the vertices in the graph. While we can have efficient algorithms to find a spanning tree(perhaps a minimum spanning tree), why cant we have algorithms for finding a hamiltonian circuit?? We can keep on adding and removing one edge at a time till we reach a cycle and perhaps, we could find a hamiltonian cycle??
The two problems are quite different. Think of the minimum spanning tree as the problem of connecting places where you only have to pay once to build the road, but you can use it as many times as you like. It's easy to come up with the cheapest configuration of roads (e.g. by Kruskal's algorithm) that allows you to travel from any place to any other.
The Hamiltonian cycle, on the other hand, wants you to minimize the actual travel distance, i.e. every move from one place to another counts. (It also asks you never to visit a place twice, but that's a minor detail.) This problem is fundamentally non-local, in the sense that you cannot tell whether you're doing the right thing just by locally exploring the options for the next step. By comparison, the greedy MST algorithm is guaranteed to pick the right next edge to add to the tree at every step.
By the way, nobody says that "we cannot have efficient algorithms for HP". It might be that we just haven't found one yet :-)
Both problems want to connect all vertices to each other.
For a minimum spanning tree you don't care to which vertex a vertex a is connected, so you can just connect a to the closest vertex. Since you only connect vertices that are not connected yet, this gives a tree, and you have your algorithm.
For a hamiltonian path however, you do care to which vertex (say b) you connect a vertex a, as you cannot use b again (otherwise it's no path anymore). So in order to determine to what vertex you should connect a, you have to try all possibilities and see what happends. That is, no one has found an efficient way yet, that of course does not automatically means there is none.
In hamiltonian path, all vertices except source and sink have a degree of 2. That is not necessarily the case with MST (or ST, if you want it).
A hamiltonian path and especially a minimum hamiltonian cycle is useful to solve a travel-salesman-problem i.e. a shortest trip. A fast solution is looking like a hilbert curve a special kind of a space-filling-curve also uses to reduce the space complexity and for efficient addressing. A mst is like connecting all vertices together with cheapest cost to connect (i.e. travel) no matter of the order or crossing. It's useful to solve a problem like finding roads, finding water-canal, finding internet-cable.
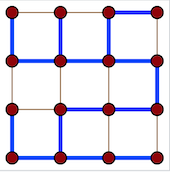
Both Spanning Tree and Hamiltonian path spans all the vertices in a Graph. A Spanning Tree may or may not be a path from s to t. The Spanning Tree on the picture is not a path.
As someone mentioned above there are some consequences, for example, in a path all degrees are 1 or 2. In the tree above you may see some vertices with degree 3.
If you are interested why there are no known polynomial time algorithm for HAMPATH I'd recommend Tim Roughgarden's book, Part 4. He calls it "MST vs. TSP: An Algorithmic Mystery".
The standard answer is that HAMPATH is an NP-complete problem. This doesn't mean there're no poly-time algorithms, but it's the most realistic scenario. Algorithms that are known for these type of problems can be quite reasonable for some instances, just not polynomial.
Hamiltonian path is a spanning tree (a special spanning tree with only 2 leave), but a spanning tree (which can have more than 2 leaves) may not be a hamiltonian cycle. With the definition differencess, you may see some different use of them.
© 2022 - 2024 — McMap. All rights reserved.