Conv1D with kernel_size=1 vs Linear layer

Question

I'm working on very sparse vectors as input. I started working with simple Linear (dense/fully connected layers) and my network yielded pretty good results (let's take accuracy as my metric here, 95.8%).

I later tried to use a Conv1d with a kernel_size=1 and a MaxPool1d, and this network works slightly better (96.4% accuracy).

Question: How are these two implementation different ? Shouldn't a Conv1d with a unit kernel_size do the same as a Linear layer?

I've tried multiple runs, the CNN always yields slightly better results.

Inherent

Yes the Conv1d does the same assuming the implementations are correct (eg to run the CNN along the right axis vs the Linear broadcasted layer you need to call inputs.transpose(1,2)), probably all comes down to the MaxPool1d – Brewing

Answer 1

nn.Conv1d with a kernel size of 1 and nn.Linear give essentially the same results. The only differences are the initialization procedure and how the operations are applied (which has some effect on the speed). Note that using a linear layer should be faster as it is implemented as a simple matrix multiplication (+ adding a broadcasted bias vector)

@RobinFrcd your answers are either different due to MaxPool1d or due to the different initialization procedure.

Here are a few experiments to prove my claims:

def count_parameters(model):
    """Count the number of parameters in a model."""
    return sum([p.numel() for p in model.parameters()])

conv = torch.nn.Conv1d(8,32,1)
print(count_parameters(conv))
# 288

linear = torch.nn.Linear(8,32)
print(count_parameters(linear))
# 288

print(conv.weight.shape)
# torch.Size([32, 8, 1])
print(linear.weight.shape)
# torch.Size([32, 8])

# use same initialization
linear.weight = torch.nn.Parameter(conv.weight.squeeze(2))
linear.bias = torch.nn.Parameter(conv.bias)

tensor = torch.randn(128,256,8)
permuted_tensor = tensor.permute(0,2,1).clone().contiguous()

out_linear = linear(tensor)
print(out_linear.mean())
# tensor(0.0067, grad_fn=<MeanBackward0>)

out_conv = conv(permuted_tensor)
print(out_conv.mean())
# tensor(0.0067, grad_fn=<MeanBackward0>)

Speed test:

%%timeit
_ = linear(tensor)
# 151 µs ± 297 ns per loop

%%timeit
_ = conv(permuted_tensor)
# 1.43 ms ± 6.33 µs per loop

As Hanchen's answer show, the results can differ very slightly due to numerical precision.

Jaret

Answer 2

I've encountered similar issues when working with 3d point clouds with models such as PointNet (CVPR'17). Therefore I've made a few more interpretations based on Yann Dubois's answers. We first define a few utility functions and then report our findings:

import torch, timeit, torch.nn as nn, matplotlib.pyplot as plt


def count_params(model):
    """Count the number of parameters in a module."""
    return sum([p.numel() for p in model.parameters()])


def compare_params(linear, conv1d):
    """Compare whether two modules have identical parameters."""
    return (linear.weight.detach().numpy() == conv1d.weight.detach().numpy().squeeze()).all() and \
           (linear.bias.detach().numpy() == conv1d.bias.detach().numpy()).all()


def compare_tensors(out_linear, out_conv1d):
    """Compare whether two tensors are identical."""
    return (out_linear.detach().numpy() == out_conv1d.permute(0, 2, 1).detach().numpy()).all()

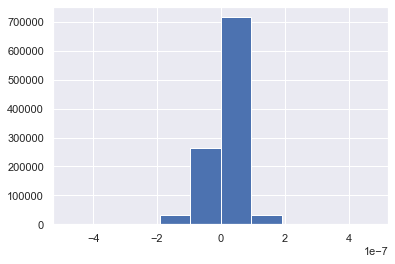
1. With the same input and parameters, nn.Conv1d and nn.Linear are expected to produce same forward results arithmetically, but experiments show that there are different. We show this by plotting the histogram of the numerical differences. Note that this numerical difference will increase as the network goes deep.

conv1d, linear = nn.Conv1d(8, 32, 1), nn.Linear(8, 32)

# same input tensor
tensor = torch.randn(128, 256, 8)
permuted_tensor = tensor.permute(0, 2, 1).clone().contiguous()

# same weights and bias
linear.weight = nn.Parameter(conv1d.weight.squeeze(2))
linear.bias = nn.Parameter(conv1d.bias)
print(compare_params(linear, conv1d))  # True

# check on the forward tensor
out_linear = linear(tensor)  # torch.Size([128, 256, 32])
out_conv1d = conv1d(permuted_tensor)  # torch.Size([128, 32, 256])
print(compare_tensors(out_linear, out_conv1d))  # False
plt.hist((out_linear.detach().numpy() - out_conv1d.permute(0, 2, 1).detach().numpy()).ravel())

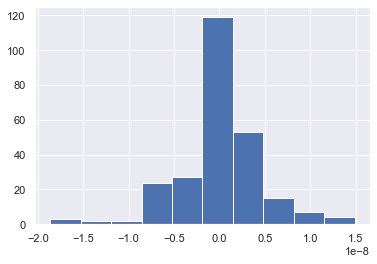
2. Gradient updates in back propagation will also be numerically different.

target = torch.randn(out_linear.shape)
permuted_target = target.permute(0, 2, 1).clone().contiguous()

loss_linear = nn.MSELoss()(target, out_linear)
loss_linear.backward()
loss_conv1d = nn.MSELoss()(permuted_target, out_conv1d)
loss_conv1d.backward()

plt.hist((linear.weight.grad.detach().numpy() - 
    conv1d.weight.grad.permute(0, 2, 1).detach().numpy()).ravel())

3. Computing Speed on GPU. nn.Linear is a bit faster than nn.Conv1d

# test execution speed on CPUs
print(timeit.timeit("_ = linear(tensor)", number=10000, setup="from __main__ import tensor, linear"))
print(timeit.timeit("_ = conv1d(permuted_tensor)", number=10000, setup="from __main__ import conv1d, permuted_tensor"))

# change everything in *.cuda(), then test speed on GPUs

Peru

can you also confirm @Inherent observation, that conv1d is better than linear? Thx – Tetanus

@arashjavanmard Yes, we found it is better. – Peru

Nice analysis! Is the linear 10 times faster as in the @Inherent observation? Have you tried implementing PointNet with both linear and conv and compare their performance, inference time and memory usage during training? – Tampere

Answer 3

Yes, they are different. I assume that you use the Pytorch API, and please read Pytorch's Conv1d. To be honest, if you take the operator as a matrix product, Conv1d with kernel size=1 does generate the same results as Linear layer. However, it should be pointed out the operator used in Conv1d is a 2D cross-correlation operator which measures the similarity of two series. I think your dataset benefits from this mechanism.

Metabolize