geom_density y-axis goes above 1

Question

I think this might partly be an R question and partly a statistics question, so please excuse me if there is a better place for it (if so, please let me know where).

Let's say I have a dataset my_measurements like this:

> glimpse(my_measurements)
Observations: 200
Variables: 2
$ sample_id <int> 18, 22, 30, 59, 74, 126, 133, 137, 147, 186, 189, 195, 203, 248, 294, 303, 320, 324, 353, 3...
$ value     <dbl> 0.9565217, 1.0000000, 0.7500000, 0.7142857, 1.0000000, 0.8571429, 1.0000000, 1.0000000, 0.8...

Where each sample_id has a corresponding measurement of something which gives a value between 0 and 1 (so e.g. they might be proportions of something).

The full dput() output for it is:

my_measurements <- tibble::tibble(
  sample_id = c(
    18L, 22L, 30L, 59L, 74L, 126L, 133L, 137L, 147L, 186L, 189L,
    195L, 203L, 248L, 294L, 303L, 320L, 324L, 353L, 375L, 384L, 385L,
    395L, 400L, 401L, 411L, 459L, 468L, 479L, 482L, 497L, 502L, 528L,
    556L, 576L, 601L, 640L, 657L, 659L, 674L, 687L, 688L, 709L, 711L,
    716L, 737L, 744L, 771L, 784L, 791L, 793L, 794L, 813L, 845L, 854L,
    864L, 866L, 887L, 891L, 899L, 915L, 917L, 919L, 934L, 948L, 969L,
    975L, 980L, 998L, 1006L, 1011L, 1015L, 1021L, 1036L, 1047L, 1056L,
    1062L, 1073L, 1074L, 1082L, 1087L, 1101L, 1102L, 1108L, 1113L,
    1119L, 1130L, 1160L, 1175L, 1176L, 1179L, 1187L, 1188L, 1206L,
    1224L, 1227L, 1411L, 1412L, 1431L, 1472L, 1481L, 1485L, 1488L,
    1491L, 1501L, 1519L, 1531L, 1534L, 1537L, 1559L, 1579L, 1592L,
    1603L, 1608L, 1629L, 1643L, 1684L, 1721L, 1726L, 1736L, 1744L,
    1756L, 1778L, 1800L, 1807L, 1813L, 1829L, 1839L, 1901L, 1905L,
    1926L, 1975L, 1980L, 2004L, 2006L, 2019L, 2062L, 2069L, 2079L,
    2087L, 2091L, 2116L, 2123L, 2141L, 2147L, 2159L, 2160L, 2163L,
    2168L, 2173L, 2191L, 2194L, 2208L, 2214L, 2231L, 2244L, 2246L,
    2253L, 2273L, 2290L, 2291L, 2302L, 2318L, 2326L, 2353L, 2371L,
    2372L, 2388L, 2412L, 2415L, 2423L, 2443L, 2451L, 2452L, 2468L,
    2470L, 2472L, 2481L, 2485L, 2502L, 2503L, 2504L, 2521L, 2572L,
    2601L, 2621L, 2625L, 2635L, 2643L, 2644L, 2674L, 2698L, 2710L,
    2723L, 2742L, 2757L, 2794L, 2824L, 2835L, 2837L
  ),
  value = c(
    0.956521739130435, 1, 0.75, 0.714285714285714, 1, 0.857142857142857, 1, 1,
    0.869565217391304, 0, 0.892857142857143, 0.9, 1, 0.892857142857143, 1, 1, 0,
    0.883333333333333, 1, 0.976190476190476, 0.973684210526316, 0.914285714285714,
    1, 0.6, 0.6, 1, 0.931818181818182, 1, 0.882352941176471, 0.75, 1, 1, 1,
    0.826086956521739, 1, 0.8, 0.75, 1, 0.931034482758621, 1, 1,
    0.980769230769231, 1, 0.875, 1, 0.985294117647059, 1, 1, 0.5,
    0.826086956521739, 0.833333333333333, 0.75, 0.631578947368421, 1, 0.875, 1, 1,
    0.904761904761905, 1, 1, 0.666666666666667, 0.96551724137931, 1,
    0.636363636363636, 1, 0.681818181818182, 0.78125, 0.285714285714286,
    0.833333333333333, 0.928571428571429, 0.991735537190083, 1, 0.5,
    0.833333333333333, 0.666666666666667, 0.8, 0.666666666666667,
    0.710526315789474, 0.787878787878788, 1, 1, 0.888888888888889, 1, 1,
    0.703703703703704, 1, 1, 0.875, 0.686274509803922, 0.714285714285714, 1, 1, 1,
    1, 1, 1, 0.805309734513274, 0.774193548387097, 1, 1, 1, 0.62962962962963, 1,
    0.782608695652174, 1, 1, 0.5, 0.666666666666667, 1, 1, 0.5, 0.5,
    0.555555555555556, 0.666666666666667, 0.5, 0.5, 0.697674418604651,
    0.593220338983051, 1, 0.6, 1, 1, 0.615384615384615, 0.673913043478261, 0.5, 1,
    1, 0, 1, 1, 0.555555555555556, 0.366666666666667, 0.333333333333333, 1, 1, 1,
    0.888888888888889, 1, 1, 1, 1, 1, 1, 0.6, 0.26530612244898, 1, 0.3, 1, 1, 0.5,
    1, 1, 1, 0.888888888888889, 0.666666666666667, 1, 1, 0.866666666666667,
    0.193548387096774, 1, 1, 0.181818181818182, 1, 1, 0.947368421052632, 1, 1, 1,
    0.851851851851852, 1, 1, 0.0769230769230769, 0.125, 0.1875, 1,
    0.230769230769231, 0.111111111111111, 1, 1, 0.444444444444444, 1, 0.5,
    0.153846153846154, 0.3, 0, 0.0714285714285714, 0.166666666666667, 1,
    0.166666666666667, 1, 0.181818181818182, 0.0714285714285714,
    0.142857142857143, 1, 0, 0, 0.888888888888889, 0, 0, 0
  ),
)

I was able to use ggplot()'s geom_histogram() to make a histogram of the distribution of values which shows me that a lot of them are close to 1:

ggplot(data = my_measurements) +
    geom_histogram(mapping = aes(x = value))

[

Then, I tried to plot the same data with geom_density():

library(ggplot2)
ggplot(data = my_measurements) +
    geom_density(mapping = aes(x = value))

What I am confused by is why does the y-axis ("density") go above 1? I had the (probably erroneous) understanding that the total area under this curve should be 1. If not, (a) how do I intepret this plot, and (b) in case I want the area under the curve to be 1, how do I do it?

Jecon

It is possible for part of a curve to be >1 and for the area under the curve to be <1 or =1. Here, the part of the curve that is above y=1 --- i.e., the part between approx. x=0.8 and x=1 --- only has a width of around 0.2. So the area of that part is approximately 0.2 * 1.8 (1.8 being a guess at the average value in that x span), or around 0.36. Add that to the area under the rest of the curve, and it looks reasonable that the total area would be 1. – Qualifier

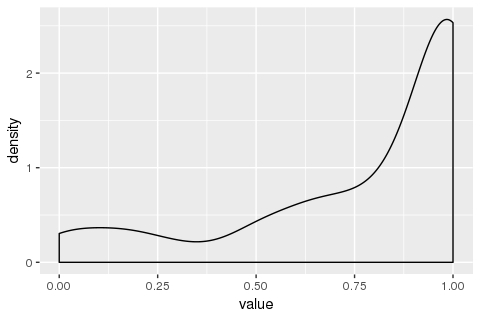
Thanks @drammock! That actually makes sense. But if so, then what does the y-axis mean? For example, at approx. x == 0.875, the corresponding y == 1.5. Surely that doesn't mean there is a 150% possibility of my x variable being 0.875, so how do I interpret y == 1.5? – Jecon

As I understand it, probability density only makes sense when integrated over an interval (along the x axis). So the value of y=1.5 would have to be multiplied by an infinitesimal width along the x-axis in order to get the probability of your variable x being exactly equal to 0.875. Maybe this will help keep it straight: the height of the curve is not probability, it is density. Probability is represented by area, so you have to multiply density by something to get probability. – Qualifier

Those last two sentences made it click for me. Thank you @drammock! Statistics lesson learned. – Jecon

Answer 1

You have to use ..scaled.. (density estimate, scaled to maximum of 1) within geom_density, by default it uses ..density...

library(ggplot2)
# In aes by default first argument is x and second argument is y
ggplot(my_measurements, aes(value, ..scaled..)) +
    geom_density()

---

All code to reproduce result:

library(ggplot2)
p1 <- ggplot(my_measurements, aes(value, ..density..)) +
    geom_density() +
    ggtitle("Density")
p2 <- ggplot(my_measurements, aes(value, ..count..)) +
    geom_density() +
    ggtitle("Count")
p3 <- ggplot(my_measurements, aes(value, ..scaled..)) +
    geom_density() +
    ggtitle("Scaled")
egg::ggarrange(p1, p2, p3, ncol = 3)

Selhorst

Thank you @PoGibas! Two more quick questions about your answer: (a) What is the ".." notation you used for "..density..", "..count..", and "..scaled.." and what does it mean? Is it used elsewhere? (b) I can see what "count" and "scaled" means, but I still don't understand how to read and understand the default "density" plot. Do you know what it means? (specifically what the y-axis means?) Thanks!! – Jecon

BTW, thanks for suggesting the use of the egg package. I didn't know it existed and will take a look. Is it comparable to cowplot? – Jecon

@Jecon You can find more info on double dot here; Density meaning is not very clear, in documentation they define it as density estimate while scaled is density estimate, scaled to maximum of 1. That Density should be calculated with density(), but how they transform those values is not clear to me; I like egg, because is solely dedicated to plot arrangement while cowplot has other functions. – Selhorst

Answer 2

I think the confusion is about discrete and continuous variables. For discrete variables all probability mass functions are in [0, 1]. For continuous variables with density, the area under the curve in 1. If a certain point has density value larger than 1, that does not imply that the particular point has probability greater than 1. Probability for that point is still zero. Value of density is combined with the range on the x-axis to calculate area under the curve. Hence, area and density value are different. Your plot is all good.

Malissamalissia