Fit Quadrilateral (Tetragon) to a blob

Question

After applying different filtering and segmentation techniques, I end up with an image like this:

I have access to some contours detection functions that return a list of points on the edge of that object, or returns a fitted polygon (with many edges though, much more than 4). I want a way to fit a quadrilateral to that shape as I know it is a front face of a shoebox that is supposed to be a quadrilateral. Due to the perspective view, the parallelity is not conserved so I have no constraints for now and just need four line segments encompassing this box.

What I could find until now was only rectangle fitting, which doesn't really returns the result I need as it forces the fitted quadrilateral to be rectangular.

If I had access to the relative angle of the camera to that shoebox and knew the distance of the shoebox from my camera, I could generate a Homography matrix and warp the image such that the shoebox appears rectangular again, but for now I have no access to such information and want to do it based purely vision.

Any known approaches for solving such a problem?

Antoinetteanton

Answer 1

Update: Dev's answer is great and deserves more votes. It's great because it includes a Python implmentation of a paper that dynamically computes the 4 points.

My answer is useful a first principles approach:

• great when getting started from scratch and trying/experimenting different approaches
• not a robust solution since it relies on working out threshold values on a case by case basis (e.g. contour simplification epsilon value, etc.).

If it's still useful to understand these base principles read along.

I recommend the following steps:

1. threshold() the image
2. dilate() the image - this will remove the black line splitting the top and bottom section and also darker artifacts on the lower part
3. findContours() using setting to retrieve only external contours(RETR_EXTERNAL) and simplify the output(CHAIN_APPROX_SIMPLE)
4. process the contours further

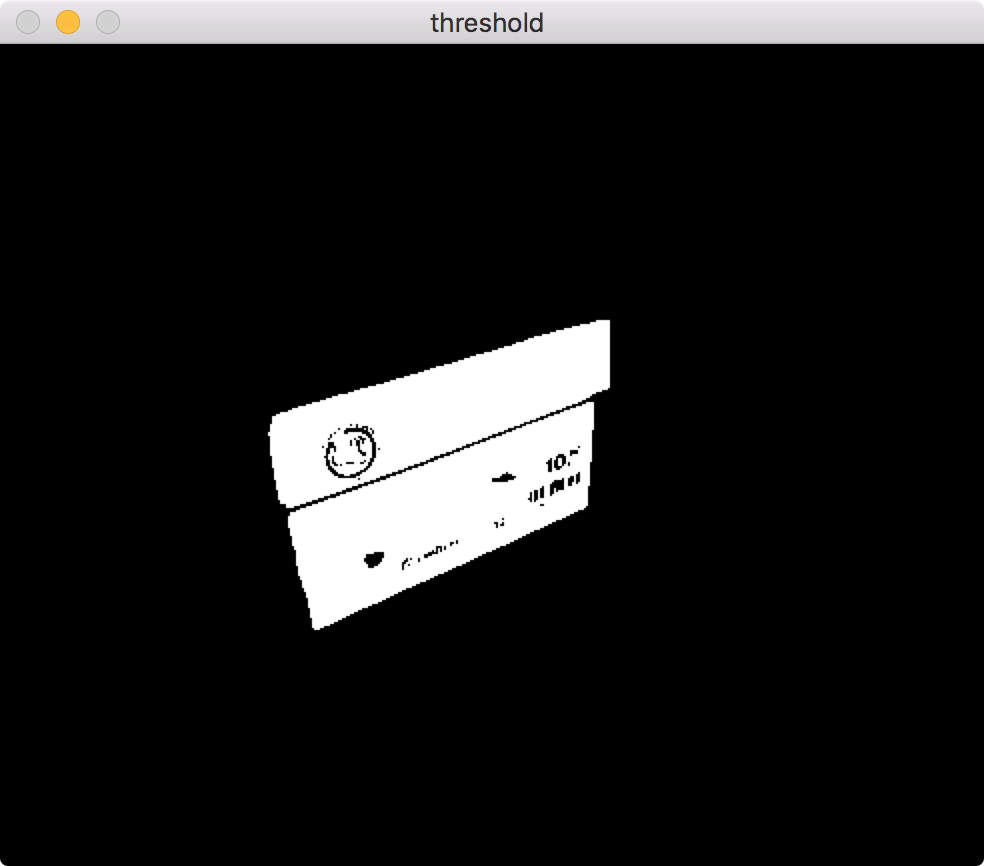
Step 1:threshold

# threshold image
ret,thresh = cv2.threshold(img,127,255,0)
cv2.imshow('threshold ',thresh)

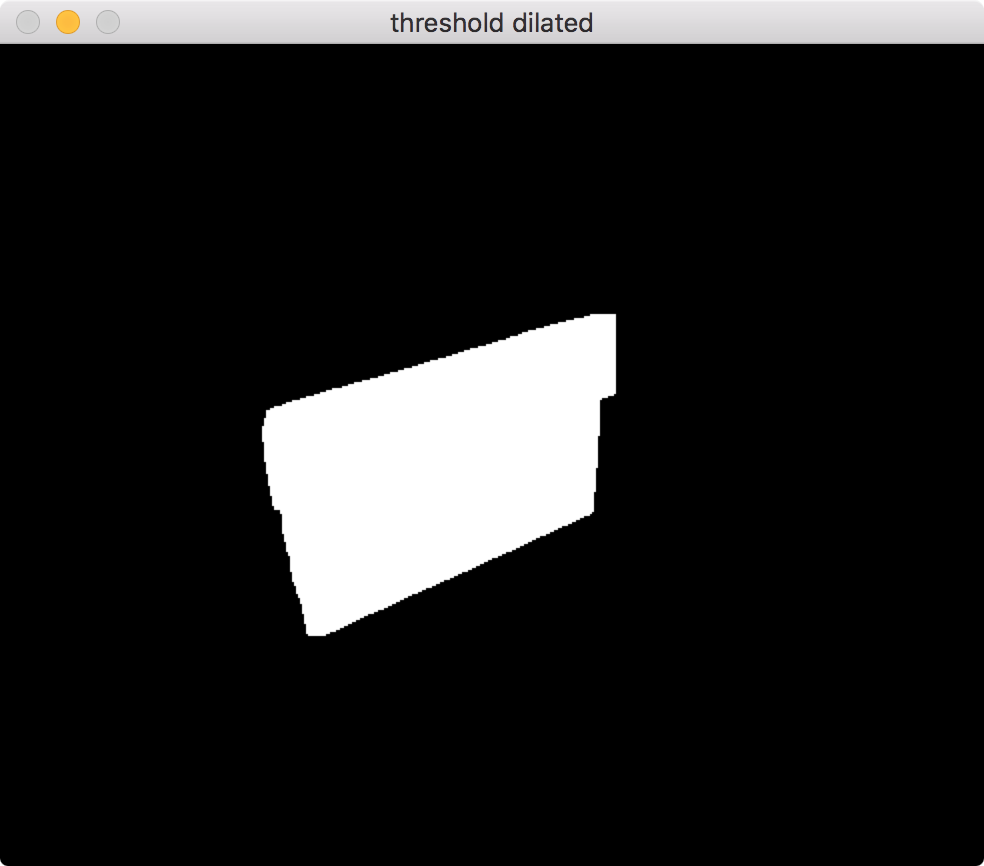
Step 2:dilate

# dilate thresholded image - merges top/bottom 
kernel = np.ones((3,3), np.uint8)
dilated = cv2.dilate(thresh, kernel, iterations=3)
cv2.imshow('threshold dilated',dilated)

Step 3: find contours

# find contours
contours, hierarchy = cv2.findContours(dilated,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(img, contours, 0, (255,255,255), 3)
print "contours:",len(contours)
print "largest contour has ",len(contours[0]),"points"

Notice that dilating first, then using simple external contours gets you shape you're after, but it's still pretty complex (containg 279 points)

From this point onward you can futher process the contour features. There are a few options, available such as:

a: getting the min. area rectangle

# minAreaRect
rect = cv2.minAreaRect(contours[0])
box = cv2.cv.BoxPoints(rect)
box = np.int0(box)
cv2.drawContours(img,[box],0,(255,255,255),3)

Can be useful, but not exactly what you need.

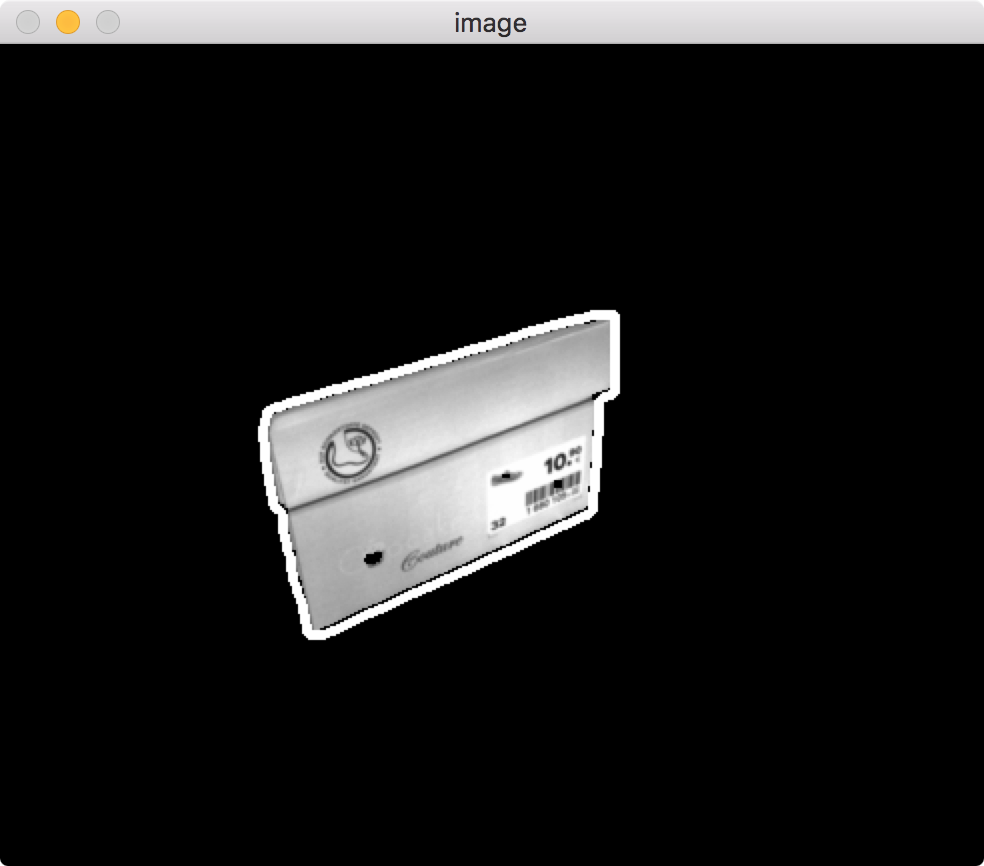
b: convex hull

# convexHull
hull = cv2.convexHull(contours[0])
cv2.drawContours(img, [hull], 0, (255,255,255), 3)
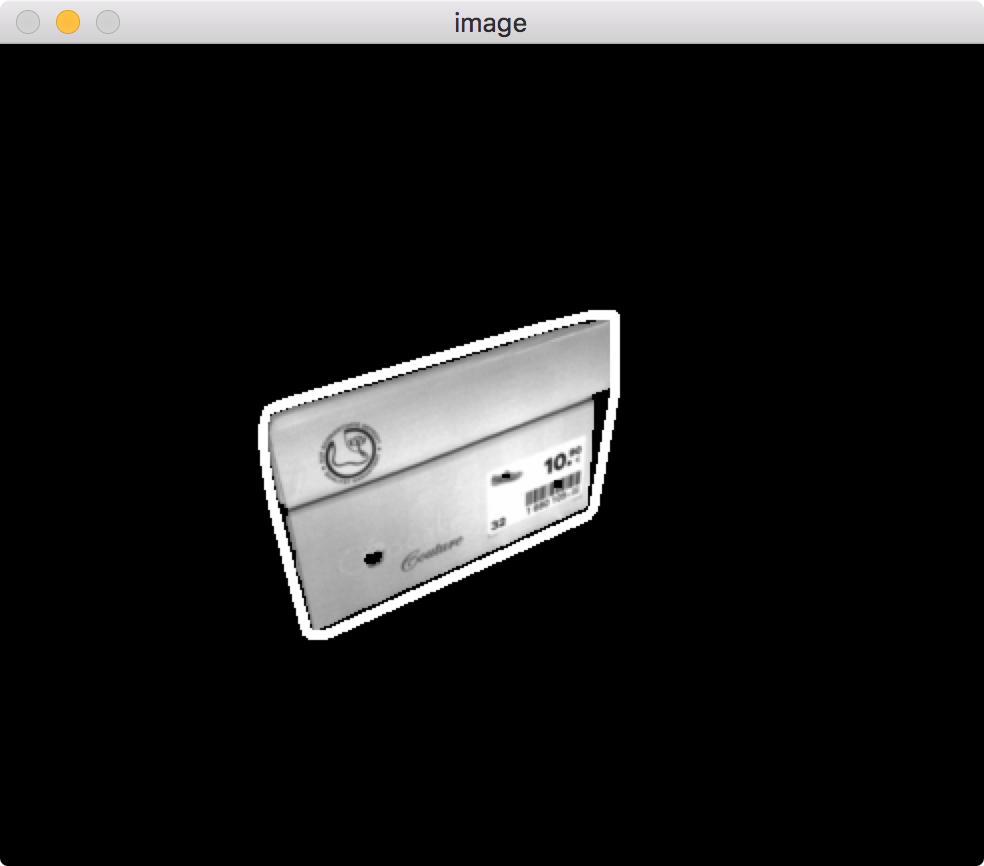
print "convex hull has ",len(hull),"points"

Better, but you still have 22 points to deal with and it's not tight as it could be

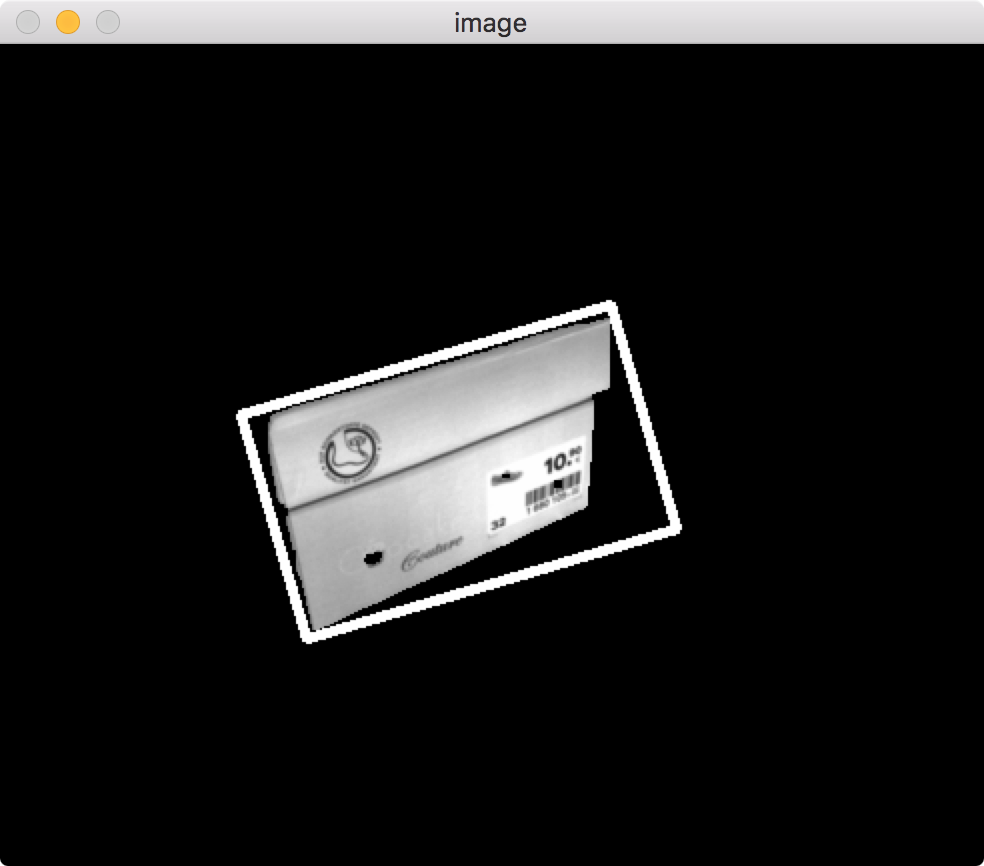
c: simplify contours

# simplify contours

epsilon = 0.1*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
cv2.drawContours(img, [approx], 0, (255,255,255), 3)
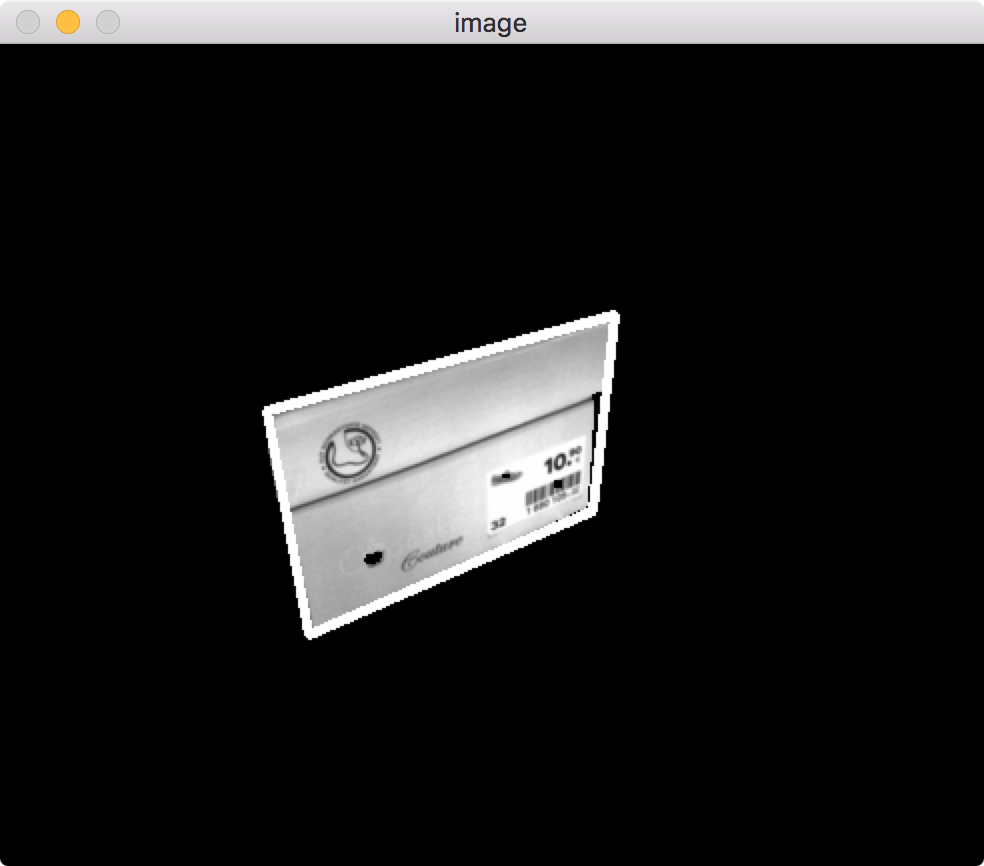
print "simplified contour has",len(approx),"points"

This is probably what you're after: just 4 points. You can play with the epsilon value if you need more points.

Bare in mind, now you have a quad, but the picture is flattened: there's no information on perspective/3d rotation.

Full OpenCV Python code listing (comment/uncomment as needed, use the reference to adapt to c++/java/etc.):

import numpy as np
import cv2

img = cv2.imread('XwzWQ.png',0)

# threshold image
ret,thresh = cv2.threshold(img,127,255,0)
cv2.imshow('threshold ',thresh)

# dilate thresholded image - merges top/bottom 
kernel = np.ones((3,3), np.uint8)
dilated = cv2.dilate(thresh, kernel, iterations=3)
cv2.imshow('threshold dilated',dilated)

# find contours
contours, hierarchy = cv2.findContours(dilated,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
# cv2.drawContours(img, contours, 0, (255,255,255), 3)
print "contours:",len(contours)
print "largest contour has ",len(contours[0]),"points"

# minAreaRect
# rect = cv2.minAreaRect(contours[0])
# box = cv2.cv.BoxPoints(rect)
# box = np.int0(box)
# cv2.drawContours(img,[box],0,(255,255,255),3)

# convexHull
# hull = cv2.convexHull(contours[0])
# cv2.drawContours(img, [hull], 0, (255,255,255), 3)
# print "convex hull has ",len(hull),"points"

# simplify contours
epsilon = 0.1*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
cv2.drawContours(img, [approx], 0, (255,255,255), 3)
print "simplified contour has",len(approx),"points"


# display output 
cv2.imshow('image',img)

cv2.waitKey(0)
cv2.destroyAllWindows()

Neurath

This is a GREAT answer! Thank YOU very much! That's what i was looking for! – Brendonbrenk

This is an outstanding answer. Thanks – Soporific

FYI, this is not guaranteed to have all original contour points inside of the quadrilateral. Sometimes DP shaves a little off. If you need to include all original points, then use the algorithm in this answer: https://mcmap.net/q/714665/-fit-quadrilateral-tetragon-to-a-blob – Diligence

Answer 2

A more accurate way to fit quadrangles to arbitrary masks is to use the technique from View Frustum Optimization To Maximize Object’s Image Area.

---

Here's the output -

---

import cv2
import numpy as np
import sympy


def appx_best_fit_ngon(mask_cv2, n: int = 4) -> list[(int, int)]:
    # convex hull of the input mask
    mask_cv2_gray = cv2.cvtColor(mask_cv2, cv2.COLOR_RGB2GRAY)
    contours, _ = cv2.findContours(
        mask_cv2_gray, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE
    )
    hull = cv2.convexHull(contours[0])
    hull = np.array(hull).reshape((len(hull), 2))

    # to sympy land
    hull = [sympy.Point(*pt) for pt in hull]

    # run until we cut down to n vertices
    while len(hull) > n:
        best_candidate = None

        # for all edges in hull ( <edge_idx_1>, <edge_idx_2> ) ->
        for edge_idx_1 in range(len(hull)):
            edge_idx_2 = (edge_idx_1 + 1) % len(hull)

            adj_idx_1 = (edge_idx_1 - 1) % len(hull)
            adj_idx_2 = (edge_idx_1 + 2) % len(hull)

            edge_pt_1 = sympy.Point(*hull[edge_idx_1])
            edge_pt_2 = sympy.Point(*hull[edge_idx_2])
            adj_pt_1 = sympy.Point(*hull[adj_idx_1])
            adj_pt_2 = sympy.Point(*hull[adj_idx_2])

            subpoly = sympy.Polygon(adj_pt_1, edge_pt_1, edge_pt_2, adj_pt_2)
            angle1 = subpoly.angles[edge_pt_1]
            angle2 = subpoly.angles[edge_pt_2]

            # we need to first make sure that the sum of the interior angles the edge
            # makes with the two adjacent edges is more than 180°
            if sympy.N(angle1 + angle2) <= sympy.pi:
                continue

            # find the new vertex if we delete this edge
            adj_edge_1 = sympy.Line(adj_pt_1, edge_pt_1)
            adj_edge_2 = sympy.Line(edge_pt_2, adj_pt_2)
            intersect = adj_edge_1.intersection(adj_edge_2)[0]

            # the area of the triangle we'll be adding
            area = sympy.N(sympy.Triangle(edge_pt_1, intersect, edge_pt_2).area)
            # should be the lowest
            if best_candidate and best_candidate[1] < area:
                continue

            # delete the edge and add the intersection of adjacent edges to the hull
            better_hull = list(hull)
            better_hull[edge_idx_1] = intersect
            del better_hull[edge_idx_2]
            best_candidate = (better_hull, area)

        if not best_candidate:
            raise ValueError("Could not find the best fit n-gon!")

        hull = best_candidate[0]

    # back to python land
    hull = [(int(x), int(y)) for x, y in hull]

    return hull

Here's the code I used to generate this image -

hull = appx_best_fit_ngon(mask_cv2)

for idx in range(len(hull)):
    next_idx = (idx + 1) % len(hull)
    cv2.line(mask_cv2, hull[idx], hull[next_idx], (0, 255, 0), 1)

for pt in hull:
    cv2.circle(mask_cv2, pt, 2, (255, 0, 0), 2)

Acquaintance

This is great! One improvement that works way better for me is always removing the shortest edge (where distance between edge_pt_1 and edge_pt_2 is smallest) instead of picking the smallest area of the new triangle. – Washerwoman