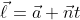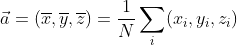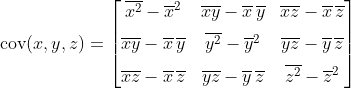3D Linear Regression

Question

I want to write a program that, given a list of points in 3D-space, represented as an array of x,y,z coordinates in floating point, outputs a best-fit line in this space. The line can/should be in the form of a unit vector and a point on the line.

The problem is that I don't know how this is to be done. The closest thing I found was this link, though quite honestly I did not understand how he went from equation to equation and by the time we got to matrices I was pretty lost.

Is there a generalization of simple 2D linear regression that I can use/can someone explain (mathematically) if/how the above linked-to method works (and what one would have to do to compute the best-fit line using it)?

Wobbly

this similar question/answer may help https://mcmap.net/q/747468/-given-n-points-on-a-2d-plane-find-the-maximum-number-of-points-that-lie-on-the-same-straight-line only 2D example is present but still the algo is suitable also for your needs. use the direction check method (in 3D encoded unit tangent vector into scalar) – Horseshit

That method wouldn't necessarily give a best fit line, would it? – Wobbly

yes but it will filter out the wrong points and get you nice starting point to speed up line fitting – Horseshit

Answer 1

Linear Regression

There is a standard formula for N-dimensional linear regression given by

Where the result, is a vector of size n + 1 giving the coefficients of the function that best fits the data.

In your case n = 3. While X is a mx(n+1) matrix called the design matrix -- in your case mx4. To construct the design matrix, you simply have to copy each data point coordinate value (x1,x2,...) into a row of X and in addition, place the number 1 in column 1 on each row. The vector y has the values associated with those coordinates. The terms and are the "transpose of X" and the "inverse of the product of the transpose of X and X." That last term can be computationally intensive to obtain because to invert a matrix is O(n^3), but for you n = 4, as long as n less than say 5000, no problem.

An example

Lets say you have data points (6,4,11) = 20, (8,5,15) = 30, (12,9,25) = 50, and (2,1,3) = 7. In that case,

Then you simply have to multiply things out and you can get directly. Multiplying matrices is straightforward and though more complicated, taking the inverse of a matrix is fairly straightforward (see here for example). However, for scientific computing languages like Matlab, Octave, and Julia (which I'll illustrate with) it's a one-liner.

julia> X = [1 6 4 11; 1 8 5 15; 1 12 9 25; 1 2 1 3]
4x4 Array{Int64,2}:
 1   6  4  11
 1   8  5  15
 1  12  9  25
 1   2  1   3

julia> y = [20;30;50;7]
4-element Array{Int64,1}:
 20
 30
 50
  7

julia> T = pinv(X'*X)*X'*y
4-element Array{Float64,1}:
  4.0
 -5.5
 -7.0
  7.0

Verifying...

julia> 12*(-5.5) + 9*(-7.0) + 25*(7) + 4
50.0

In Julia, Matlab, and Octave matrices can be multiplied simply by using *, while the transpose operator is '. Note here that I used pinv (the pseudo inverse) which is necessary (not this time) when the data is too redundant and gives rise to a non invertable X-Xtranspose, keep that in mind if you choose to implement matrix inversion yourself.

Instead PCA

Principal Component Analysis (PCA) is a technique for dimensionality reduction, the object is to find a k-dimensional space from an n dimensional space such that the projection error is minimized. In the general case, n and k are arbitrary, but in this case n = 3 and k = 1. There are 4 main steps.

Step 1: Data preprocessing

For the standard method to work, one must first perform mean normalization and also possibly scale the data so that the algorithm doesn't fail from floating point error. In the latter case, that means if the range of values of one dimension are huge relative to another there could be problem (like -1000 to 1000 in one dimension versus -0.1 to 0.2). Usually they're close enough though.Mean normalization simply mean for each dimension, subtract the average from each datapoint so that the resulting data set is centered around the origin. Take the result and store each data point (x1,x2,...xn) as a row in one big matrix X.

X = [ 6 4 11; 8 5 15; 12 9 25; 2 1 3]
4x3 Array{Int64,2}:
  6  4  11
  8  5  15
 12  9  25
  2  1   3

find the averages

y = convert(Array{Float64,1},([sum(X[1:4,x]) for x = 1:3])/4')
3-element Array{Float64,1}:
  7.0 
 4.75
 13.5 

Normalize...

julia> Xm = X .- y'
4x3 Array{Float64,2}:
 -1.0  -0.75   -2.5
  1.0   0.25    1.5
  5.0   4.25   11.5
 -5.0  -3.75  -10.5

Step 2: Calculate to covariance matrix

The covariance matrix sigma is simply

where m is the number of data points.

Step 3: Perform singular value decomposition

Here it's best to just find a library that takes the covariance matrix and spits out the answer. There are many and here are some of them; in python in R, in Java, and of course in Octave, Julia, Matlab (like R) it's another one liner svd.

Perform SVD on the covariance matrix

(U,S,V) = svd((1/4)*Xm'*Xm);

Step 4: Find the line

Take the first component (for k dimensions, you would take the first k components)

Ureduce = U[:,1]
3-element Array{Float64,1}:
 -0.393041
 -0.311878
 -0.865015

This is the line that minimizes the projection error

Extra Credit: Going back

You can even recover the approximation of the original values, but they will all be lined up and projected on the same line. Connect the dots to get a line segment.

Obtain the reduced dimension of each of the data points in X (since 1-D will each be 1 value):

z= Ureduce' * Xm'
1x4 Array{Float64,2}:
2.78949  -1.76853  -13.2384  12.2174

Go back the other way; the original values but all lying on the same (optimal) line

julia> (Ureduce .* z .+ y)'
4x3 Array{Float64,2}:
  5.90362  3.88002   11.0871                         6  4  11
  7.69511  5.30157   15.0298      versus             8  5  15
 12.2032   8.87875   24.9514                        12  9  25
  2.19806  0.939664   2.93176                        2  1   3

Malfeasance

While this is helpful, there are multiple things that are unclear to me. First, Theta seems to give the equation of a plane, rather than a line in 3D (based on the example), which is what I require. Second, I definitely have more than 4 points, which would make X a non-square matrix. Would that matter (I assume it won't if I use the pseudo-inverse, but I wanted to make sure)? Third, it seems unclear to me what exactly the values of Y are. You said it is the values associated with the points, but all I have as input are the points themselves. – Wobbly

@Wobbly This works with any number of points, m. For though X might not be square, X-transpose times X will be. As for the dimensionality, now that I think about it, your situation is y = f(x1,x2) rather than y = f(x1,x2,x3), so just reduce the dimensionality by 1. But you're right, regression is meant to answer what equation best satisfies how to predict z given x and y, and that will be a plane. It seems now what you really want is PCA with dimensionality reduced to 1 (a line). – Malfeasance

So if I reduce the dimensionality by 1, what is the Y vector then? – Wobbly

@Wobbly assuming you have f(x,y) = z, and you want to create a regression where you have x,y, but want the program to find the best z based on the data, then the unfortunately named "y" vector contains all of the z's. and the X matrix contains the x's and y's. – Malfeasance

I'll check that out. I was thinking of finding the best fit plane for the set of (x,y,z) coordinates, and then projecting them on the plane and doing normal 2D linear regression and taking that line. The PCA seemed too convoluted. – Wobbly

@Wobbly It's funny that you say you want to do that, because what PCA does is take a space of dimension n and reduce it to dimension k so that the projection error is minimized. Except instead of doing so iteratively, it does so all at once. The math behind why it works can be daunting, but the algorithm itself is not that hard. I'll add to the answer a section on PCA. – Malfeasance

@Malfeasance I suddenly feel an urge to buy you a beer. – Artamas

@Artamas Oh man, I knew this whole stackoverflow thing would eventually pay off! – Malfeasance

@Malfeasance Although I'm slightly stumped as to why the three values in step 4 would represent the values of a line in three dimensions. How could I use these three values to establish a (x,y) -> (z) function? – Artamas

Somebody give this person a cookie, cause (s)he deserves a cookie! – Manslayer

@DennisBraga how do you get a line out of the last part? like easymoden00b said? – Archivolt

What is "(6,4,11) = 20" ? – Ramer

Answer 2

Great answer by @WaTeim

here is my contribution in python for those who need it. works with the numerical example provided

def regr(X):
    y= np.average(X, axis=0)
    Xm = X-y
    u, s, v = np.linalg.svd((1./X.shape[0])*np.matmul(Xm.T,Xm))

    # Extra Credit: Going back
    z= np.matmul(u[:,0].T, Xm.T)
    c = np.array([z*n for n in u[:,0]])
    d = np.array(y.tolist()*c.shape[1]).reshape(c.shape[1],-1).T
    e = (c+d).T
    return u,s,v

regr(np.array([[6, 4, 11],[8,5,15],[12,9,25],[2,1,3]]))

btw. Can anyone tell me why numpy's np.cov() gives different result than 1./X.shape[0])*np.matmul(Xm.T,Xm) ???

Bibbie

Answer 3

Finding the best fitting line for the given a list of points in 3D-space is a quite difficult task. One can define a line in 3D-space using 2 vectors: point a, which lies on the line, and line (normalized) direction n . It can be described by the following equation, where t is real number

Assuming that one has list of points {(xᵢ, yᵢ, zᵢ)}, point a can be expressed by mean value of all points, i.e.

while direction n can be found by solving eigenproblem for covariance matrix

After solving the eigenequation, one can take eigenvector corresponding to the largest eigenvalue, which corresponds to the solution n.

This is my demo for set of points {(1,1,1), (2,2,2), (3,3,3)} using Armadillo library (C++):

#include<armadillo>
#include<vector>
using namespace arma;

int main()
{
    std::vector<vec3> points {{ 
        {1, 1, 1}, 
        {2, 2, 2}, 
        {3, 3, 3} 
    }};
    int N = points.size();

    vec3 mean = {0, 0, 0};
    mat33 corr(fill::zeros);
    for(auto p : points)
    {
        mean += p;
        for(int i = 0; i < 3; i++)
            for(int j = i; j < 3; j++)
                corr(i, j) += p(i) * p(j);
    }

    corr /= N;
    mean /= N;

    mat33 cov {{
        {corr(0, 0) - mean(0) * mean(0), corr(0, 1) - mean(0) * mean(1), corr(0, 2) - mean(0) * mean(2)},
        {corr(0, 1) - mean(0) * mean(1), corr(1, 1) - mean(1) * mean(1), corr(1, 2) - mean(1) * mean(2)},
        {corr(0, 2) - mean(0) * mean(2), corr(1, 2) - mean(2) * mean(1), corr(2, 2) - mean(2) * mean(2)}
    }};

    vec3 eigval; mat33 eigvec;
    eig_sym(eigval, eigvec, cov);

    mean.print("\nPoint: ");

    eigvec.col(eigval.index_max())
          .print("\nDirection:");
}

Zimbabwe

Finally s.o. writing down the task, thank you! – Ramer

Answer 4

This can be achieved with a NPM ml-matrix one-liner:

const { Matrix, solve } = require('ml-matrix');

solve(this.DataX, Matrix.columnVector(this.DataY[0]));

Lotson

The question is language-agnostic, so at least you could say what language you are refering to… – Signalment

My guess would be JavaScript because of the reference to npm if that helps at all @m93a – Monecious

Answer 5

I use this simple method in QT code:

QPair<QVector3D, QVector3D> getLineByLeastSquares(const QVector<QVector3D>& points)
{
    if (points.size() <= 1)
        return QPair<QVector3D, QVector3D>();
    QVector3D avg;
    for (const QVector3D& p : points)
        avg += p;
    avg /= static_cast<float>(points.size());
    float nX = 0.0F, nY = 0.0F, nZ = 0.0F;
    for (const QVector3D& p : points)
    {
        const QVector3D tmp = p - avg;
        nX += tmp.x() * tmp.x();
        nY += tmp.x() * tmp.y();
        nZ += tmp.x() * tmp.z();
    }
    return QPair<QVector3D, QVector3D>(avg, QVector3D(nX, nY, nZ).normalized());
}

First component of result QPair<QVector3D, QVector3D> is line point and second is line normal.

Bibby