Programming for Young tableaux

Question

A strange question follows:
I'm doing a problem solving competition @ my school, and they allow us to use a computer. Since I'm the only one in the competition who knows how to code, I use C and Pascal programs to solve problems faster. I've done that with pseudocode-to-code exercises, algorithms, Collatz conjecture verification and such.
Now, yesterday I was training for the next challenge (18th of April), and I saw an exercise on Young tableaux. It was phrased like this(I'll do my best to translate from Italian):
"Ferrers diagrams are configuration of N boxes distributed in one or more horizontal rows, left-aligned and configured so that every row contains an equal or lower number of boxes than the row over it. These configurations might also be described by a list of the boxes' number, like in this image:

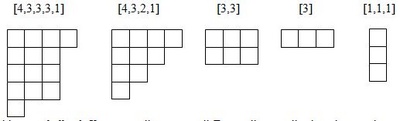
_{(source: olimpiadiproblemsolving.it)}

A Young tableau is a Ferrers diagram of N boxes filled with integers from 1 to N. Example:

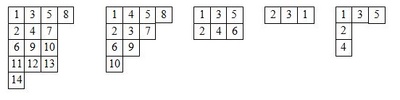
_{(source: olimpiadiproblemsolving.it)}

If numbers in the boxes are sorted so that they are in increasing order by row and by column, the table is "standard"(example: first, third and fifth tableau). In standard tableaux, the first box of the first row always contains 1. N is always in the left-most box in one of the rows of the diagram.


PROBLEM

Consider a [6,3,2,1,1,1] Ferrers diagram:
1) If 6 is fixed on the 6th box of the 1st row and 11 is fixed in the last box of the 1st column, in how many ways can you complete the diagram in a standard way?

2) If 7 is fixed on the 6th box of the 1st row and 11 is fixed in the last box of the 1st column, in how many ways can you complete the diagram in a standard way?

3) If 8 is fixed on the 6th box of the 1st row and 11 is fixed in the last box of the 1st column, in how many ways can you complete the diagram in a standard way?"

I've tried to code a solution with a matrix filled with those numbers and with "-1" as a "row-ending character", but I got stuck. How can I code "fill it in every way possible so that the tableau is standard?".

Rickard

For this, Prolog would be a better choice of a tool than C, I think. – Arguello

It's been a long time I've seen such a well-phrased question here. Here, take my last upvote today. – Depolymerize

Ehm...what is Prolog? – Rickard

Think about how you might count the number of ways to fill it without actually generating solutions. Dynamic programming, memoization, and recursion will be your friends. Since the other competitors aren't using programs, there must be a solution that doesn't involve a huge amount of computation. Great question! – Refraction

Drawing the tableau, I noticed that it looks the same way if I rotate the paper sheet where I drawn it 90° clockwise. Also, in the first column there can be any number between 1 and 11 except 1,6 and 11, and in the first row any number between 1 and 6 except 1 and 6. And there are 14 boxes, so N=14. Hmm. – Rickard

The last requirement of a standard Young tableau implies the last row can only have one column. Is that what you intended? – Flintshire

So you already have an advantage over the other competitors, being the only one using a computer, and that's not enough. You also wants SO users to help you beat them. Fight fair. ;-) – Affiant

Hey, we're not even the best ones. I mean, I'm the only one in the school who knows how to code, but my team's arrived 15th in the region(I live in Italy). We're going for the regional challenge 18th of April, and we need to solve at least 2 more exercises to beat the 1st. One is this, for the other one I'm working with my IT teacher to write a Dijkstra's alg. program. – Rickard

Answer 1

Here is a sample solution using SWI-Prolog for the first problem:

:- use_module(library(clpfd)).

tableau(Ts) :-
        Ts = [[A,B,C,_,_,F],
              [G,H,I],
              [J,K],
              [L],
              [M],
              [N]],
        A = 1,
        maplist(ascending, Ts),
        ascending([A,G,J,L,M,N]),
        ascending([B,H,K]),
        C #< I,
        append(Ts, Vs),
        all_different(Vs),
        Vs ins 1..14,
        F = 6,
        N = 11,
        label(Vs).

ascending(Vs) :- chain(Vs, #<).

The answer is that there are 2 ways to complete the tableau:

?- tableau(Ts), maplist(writeln, Ts).
[1,2,3,4,5,6]
[7,12,13]
[8,14]
[9]
[10]
[11]
    Ts = [[1, 2, 3, 4, 5, 6], [7, 12, 13], [8, 14], [9], [10], [11]] ;
[1,2,3,4,5,6]
[7,12,14]
[8,13]
[9]
[10]
[11]
    Ts = [[1, 2, 3, 4, 5, 6], [7, 12, 14], [8, 13], [9], [10], [11]] ;
false.

Hygro

Thanks a lot! This one works consulting it with SWIProlog and I've learned to manipulate it for any problem with Young tableaux! Thanks again! – Rickard

Answer 2

To solve this I would use Constraint Programming (CP). The Young tableaux is actually one of the standard problems that I try to solve when learning a new CP system. Here's a list of the implementations so far: http://hakank.org/common_cp_models/#youngtableaux .

I have changed the "plain" MiniZinc model with some extra constraints for your specific questions. See the full model here: http://www.hakank.org/minizinc/young_tableaux_stack_overflow.mzn

(MiniZinc is very high level and easy to experiment with for problems like this.)

Short about the representation in the model: For a problem of size n (partition of n), the boxes are represented as a grid ("x", sized n times n) with the values of 1 to n+1, where each row and column are sorted in increasing order; so n+1 is sorted last and act as an empty value. The partition structure ("p") is then handled to comply with the Young/Ferrer structure (see the model for details).

Each of the three questions has two extra constraints (compared to the standard formulation of the problem):

• a certain number should be in the 6th box of the first row The added constraint is x[1,6] = 6 % or 7 or 8

• and 11 should be in the last box of the first column This is a little bit trickier but my way is this, i.e. that in the first column 11 should be last of the values less than n+1, i.e. all values following in the column are n+1:

   exists(j in 1..n) (
        x[j,1] = 11 /\ forall(k in j+1..n) (x[k,1] = n+1)
   )
  

So, if I've understood the questions correctly the answers are: 1) 2 solutions 2) 10 solutions 3) 30 solutions

Herring

Very interesting link! I've never heard of any of the CP systems mentioned there, or of CP itself, but looks interesting. I'll look into it. Thanks. – Rickard

Constraint propagation is good to know for many classes of puzzles or problems. When I'm learning a new language, I typically port Peter Norvig's Sudoku solver in Python. Worth a read, and is a small introduction to constraint propagation. – Aparicio

Answer 3

Without using a program, I believe the answer to 1) is 2. Deriving this by hand might lead someone to an algorithmic solution.

The first row starts with 1 and ends with 6. Therefore the numbers that can go into row 1 must satisfy this condition: 1 < x < 6. Of the 14 digits that can go into this tableaux, only 4 satisfy that condition, and they are: 2 3 4 5. This means that row 1 must be: 1 2 3 4 5 6.

The first column starts with 1 and ends with 11. The numbers that can go into the first column must satisfy a similar condition: 1 < y < 11. Of the remaining unassigned numbers, only 4 meet this condition: 7 8 9 10. This leads to the first column being: 1 7 8 9 10 11.

There are only 3 remaining numbers now: 12 13 14. There are only two ways to arrange them in the remaining 3 cells of the tableaux. They can be arranged:

12 13

14

-- or --

12 14

13

Trying to tackle this in code, one could go the brute force route, or go look into constraint propagation and backtracking techniques. This is why someone suggested Prolog earlier. Another language to look at would be Python.

Aparicio

I just noticed that also, was refreshing the page to add this to the question. The 1st row must be 1 2 3 4 5 6. The 1st column must be 1 ? ? 9 10 11, because the 4th and 5th row are made of 1 box. This is also true for 2) and 3), which just add more possible numbers to the 1st row. The solution you've just written has a problem: in 2) and 3) you can't write the 1st column as 1 7 8 9 10 11 because 7 is assigned in 2) and 8 is assigned in 3). If you invert 7 and 6 in 2) and 6 and 8 in 3)(inverting also 6 and 7 so that the 1st column is 1 6 7 9 10 11), the answer to 2) and 3) is 2, too. – Rickard

Does this mean that in a [6,3,2,1,1,1] tableau where 11 is fixed in the last box of the 1st column and where any number <11 is fixed in the last box of the 1st row has 2 standard solutions? – Rickard

I've already found 6 solutions for a tableaux that meets your initial constraints. The tableaux I'm trying is: 8 is in the last cell of the first row, and 11 in the last cell of the first column. There a very likely more than 6 solutions, but I've reached the end of my break here at work. :) – Aparicio

OK, what I've written as a comment to this is false. Thanks ;) Also, to do it in C, I would have to write a lot of functions and I think it would be very inefficient, too. – Rickard

Answer 4

This is a Constraint logic programming problem. Use the Programming language Prolog. Sicstus prolog with the clpfd library.

Considering the layout as such:

ABCDEF
GHI
JK
L
M
N

--Code--

use_module(library(clpfd)).

all_different([A,B,C,D,E,F,G,H,I,J,K,L,M,N]),
domain([A,B,C,D,E,F,G,H,I,J,K,L,M,N],1,14),
B #> A, C #> B, D #> C, E #> D, F #> E,
G #> A, H #> B, H #> G, I #> G, I #> H,  I #> C,
J #> A, J #> G, 
L #> A, L #> G, L #> J,
M #> A, M #> G, M #> J, M #> L,
N #> A, N #> G, N #> J, N #> L, N #> M.

A=1
F=6
N=11

Tricia

I tried copypasting this in a file and consulting it with SWIProlog but it gives me an unexpected-end-of-file error. What should I do? I tried googling, but nothing. :( – Rickard

Answer 5

This is an excercise from famous Cormen book. I find this resource as helpful learning this problem, and make this kind of structure, and extract min element, and maintain the data structure as it is.

Oribella