I add an other answer for your question :
The CSV I posted was actually modified, my original one also contains a list for each rider with their score for each stage. This list looks like this [0, 40, 13, 0, 2, 55, 1, 17, 0, 14]. I am trying to find the team that performs the best overall. So I have a pool of 16 cyclists, from which the score of 10 cyclists counts towards the score of each day. The scores for each day are then summed to get a total score. The purpose is to get this final total score as high as possible.
If you think I should edit my first post please let me know, I think that it is more clear like this because my first post is quite dense and answers the initial question.
Let's introduce a new variable :
Zik = 1 if cyclist i is selected and is one of the top 10 in your team on day k
You need to add these constraints to link variables Zik and Xi (variable Zik cannot be = 1 if cyclist i is not selected i.e if Xi = 0)
For all i, sum(Zik, 1<=k<=n_days) <= n_days * Xi
And these constraints to select 10 cyclists per day :
For all k, sum(Zik, 1<=i<=n_cyclists) <= 10
Finally, your objective could be written like this :
Maximize sum(pik * Xi * Zik, 1<=i<=n_cyclists, 1 <= k <= n_days)
# where pik = nb_points of cyclist i at day k
And here is the thinking part. An objective written like this is not linear (notice the multiplication between the two variables X and Z). Fortunately, there are both binaries and there is a trick to transform this formula to its linear form.
![enter image description here]()
Let's introduce again new variables Lik (Lik = Xi * Zik) to linearize the objective.
The objective can now be written like this and be linear :
Maximize sum(pik * Lik, 1<=i<=n_cyclists, 1 <= k <= n_days)
# where pik = nb_points of cyclist i at day k
And we need now to add these constraints to make Lik equal to Xi * Zik :
For all i,k : Xi + Zik - 1 <= Lik
For all i,k : Lik <= 1/2 * (Xi + Zik)
And voilà. This is the beauty of mathematics, you can model a lot of things with linear equations. I presented advanced notions and it is normal if you don't understand them at first glance.
I simulated the score per day column on this file.
Here is the Python code to solve the new problem :
import ast
from ortools.linear_solver import pywraplp
import pandas as pd
solver = pywraplp.Solver('cyclist', pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
cyclist_df = pd.read_csv('cyclists_day.csv')
cyclist_df['Punten_day'] = cyclist_df['Punten_day'].apply(ast.literal_eval)
# Variables
variables_name = {}
variables_team = {}
variables_name_per_day = {}
variables_linear = {}
for _, row in cyclist_df.iterrows():
variables_name[row['Naam']] = solver.IntVar(0, 1, 'x_{}'.format(row['Naam']))
if row['Ploeg'] not in variables_team:
variables_team[row['Ploeg']] = solver.IntVar(0, solver.infinity(), 'y_{}'.format(row['Ploeg']))
for k in range(10):
variables_name_per_day[(row['Naam'], k)] = solver.IntVar(0, 1, 'z_{}_{}'.format(row['Naam'], k))
variables_linear[(row['Naam'], k)] = solver.IntVar(0, 1, 'l_{}_{}'.format(row['Naam'], k))
# Link cyclist <-> team
for team, var in variables_team.items():
constraint = solver.Constraint(0, solver.infinity())
constraint.SetCoefficient(var, 1)
for cyclist in cyclist_df[cyclist_df.Ploeg == team]['Naam']:
constraint.SetCoefficient(variables_name[cyclist], -1)
# Max 4 cyclist per team
for team, var in variables_team.items():
constraint = solver.Constraint(0, 4)
constraint.SetCoefficient(var, 1)
# Max cyclists
constraint_max_cyclists = solver.Constraint(16, 16)
for cyclist in variables_name.values():
constraint_max_cyclists.SetCoefficient(cyclist, 1)
# Max cost
constraint_max_cost = solver.Constraint(0, 100)
for _, row in cyclist_df.iterrows():
constraint_max_cost.SetCoefficient(variables_name[row['Naam']], row['Waarde'])
# Link Zik and Xi
for name, cyclist in variables_name.items():
constraint_link_cyclist_day = solver.Constraint(-solver.infinity(), 0)
constraint_link_cyclist_day.SetCoefficient(cyclist, - 10)
for k in range(10):
constraint_link_cyclist_day.SetCoefficient(variables_name_per_day[name, k], 1)
# Min/Max 10 cyclists per day
for k in range(10):
constraint_cyclist_per_day = solver.Constraint(10, 10)
for name in cyclist_df.Naam:
constraint_cyclist_per_day.SetCoefficient(variables_name_per_day[name, k], 1)
# Linearization constraints
for name, cyclist in variables_name.items():
for k in range(10):
constraint_linearization1 = solver.Constraint(-solver.infinity(), 1)
constraint_linearization2 = solver.Constraint(-solver.infinity(), 0)
constraint_linearization1.SetCoefficient(cyclist, 1)
constraint_linearization1.SetCoefficient(variables_name_per_day[name, k], 1)
constraint_linearization1.SetCoefficient(variables_linear[name, k], -1)
constraint_linearization2.SetCoefficient(cyclist, -1/2)
constraint_linearization2.SetCoefficient(variables_name_per_day[name, k], -1/2)
constraint_linearization2.SetCoefficient(variables_linear[name, k], 1)
# Objective
objective = solver.Objective()
objective.SetMaximization()
for _, row in cyclist_df.iterrows():
for k in range(10):
objective.SetCoefficient(variables_linear[row['Naam'], k], row['Punten_day'][k])
solver.Solve()
chosen_cyclists = [key for key, variable in variables_name.items() if variable.solution_value() > 0.5]
print('\n'.join(chosen_cyclists))
for k in range(10):
print('\nDay {} :'.format(k + 1))
chosen_cyclists_day = [name for (name, day), variable in variables_name_per_day.items()
if (day == k and variable.solution_value() > 0.5)]
assert len(chosen_cyclists_day) == 10
assert all(chosen_cyclists_day[i] in chosen_cyclists for i in range(10))
print('\n'.join(chosen_cyclists_day))
Here are the results :
Your team :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
ALAPHILIPPE Julian
PINOT Thibaut
MATTHEWS Michael
TRENTIN Matteo
COLBRELLI Sonny
VAN AVERMAET Greg
STUYVEN Jasper
BENOOT Tiesj
CICCONE Giulio
TEUNISSEN Mike
HERRADA Jesús
MEURISSE Xandro
GRELLIER Fabien
Selected cyclists per day
Day 1 :
SAGAN Peter
VIVIANI Elia
ALAPHILIPPE Julian
MATTHEWS Michael
COLBRELLI Sonny
VAN AVERMAET Greg
STUYVEN Jasper
CICCONE Giulio
TEUNISSEN Mike
HERRADA Jesús
Day 2 :
SAGAN Peter
ALAPHILIPPE Julian
MATTHEWS Michael
TRENTIN Matteo
COLBRELLI Sonny
VAN AVERMAET Greg
STUYVEN Jasper
TEUNISSEN Mike
NIZZOLO Giacomo
MEURISSE Xandro
Day 3 :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
MATTHEWS Michael
TRENTIN Matteo
VAN AVERMAET Greg
STUYVEN Jasper
CICCONE Giulio
TEUNISSEN Mike
HERRADA Jesús
Day 4 :
SAGAN Peter
VIVIANI Elia
PINOT Thibaut
MATTHEWS Michael
TRENTIN Matteo
COLBRELLI Sonny
VAN AVERMAET Greg
STUYVEN Jasper
TEUNISSEN Mike
HERRADA Jesús
Day 5 :
SAGAN Peter
VIVIANI Elia
ALAPHILIPPE Julian
PINOT Thibaut
MATTHEWS Michael
TRENTIN Matteo
COLBRELLI Sonny
VAN AVERMAET Greg
CICCONE Giulio
HERRADA Jesús
Day 6 :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
ALAPHILIPPE Julian
MATTHEWS Michael
TRENTIN Matteo
COLBRELLI Sonny
STUYVEN Jasper
CICCONE Giulio
TEUNISSEN Mike
Day 7 :
SAGAN Peter
VIVIANI Elia
ALAPHILIPPE Julian
MATTHEWS Michael
COLBRELLI Sonny
VAN AVERMAET Greg
STUYVEN Jasper
TEUNISSEN Mike
HERRADA Jesús
MEURISSE Xandro
Day 8 :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
ALAPHILIPPE Julian
MATTHEWS Michael
STUYVEN Jasper
TEUNISSEN Mike
HERRADA Jesús
NIZZOLO Giacomo
MEURISSE Xandro
Day 9 :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
ALAPHILIPPE Julian
PINOT Thibaut
TRENTIN Matteo
COLBRELLI Sonny
VAN AVERMAET Greg
TEUNISSEN Mike
HERRADA Jesús
Day 10 :
SAGAN Peter
GROENEWEGEN Dylan
VIVIANI Elia
PINOT Thibaut
COLBRELLI Sonny
STUYVEN Jasper
CICCONE Giulio
TEUNISSEN Mike
HERRADA Jesús
NIZZOLO Giacomo
Let's compare the results of answer 1 and answer 2 print(solver.Objective().Value()):
You get 3738.0 with the first model, 3129.087388325567 with the second one. The value is lower because you select only 10 cyclists per stage instead of 16.
Now if keep the first solution and use the new scoring method, we get 3122.9477585307413
We could consider that the first model is good enough : we didn't have to introduce new variables/constraints, model stays simple and we got a solution almost as good as the complex model. Sometimes it is not necessary to be 100% accurate and a model can be solved more easily and quickly with some approximations.

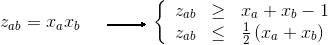
max_4_from_same_team, ortotal_cost<=100? Given that Value=6.5 is up at the 86th quantile,max_4_from_same_teamis more restraining. We could use a generator-based solution to yield those. – Vassily