scipy curve_fit raises "OptimizeWarning: Covariance of the parameters could not be estimated"

Question

I am trying to fit this function to some data:

But when I use my code

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

def f(x, start, end):
    res = np.empty_like(x)
    res[x < start] =-1
    res[x > end] = 1
    linear = np.all([[start <= x], [x <= end]], axis=0)[0]
    res[linear] = np.linspace(-1., 1., num=np.sum(linear))
    return res

if __name__ == '__main__':

    xdata = np.linspace(0., 1000., 1000)
    ydata = -np.ones(1000)
    ydata[500:1000] = 1.
    ydata = ydata + np.random.normal(0., 0.25, len(ydata))

    popt, pcov = curve_fit(f, xdata, ydata, p0=[495., 505.])
    print(popt, pcov)
    plt.figure()
    plt.plot(xdata, f(xdata, *popt), 'r-', label='fit')
    plt.plot(xdata, ydata, 'b-', label='data')
    plt.show()

I get the warning

OptimizeWarning: Covariance of the parameters could not be estimated

Output:

In this example start and end should be closer to 500, but they don't change at all from my initial guess.

Crossroad

Here is a similar question – Feme

Answer 1

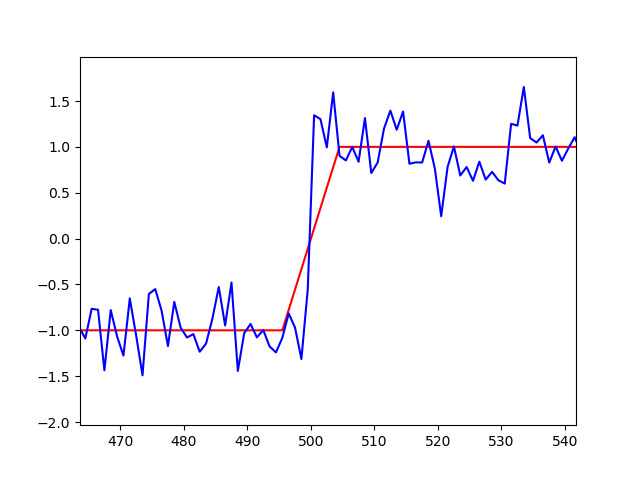
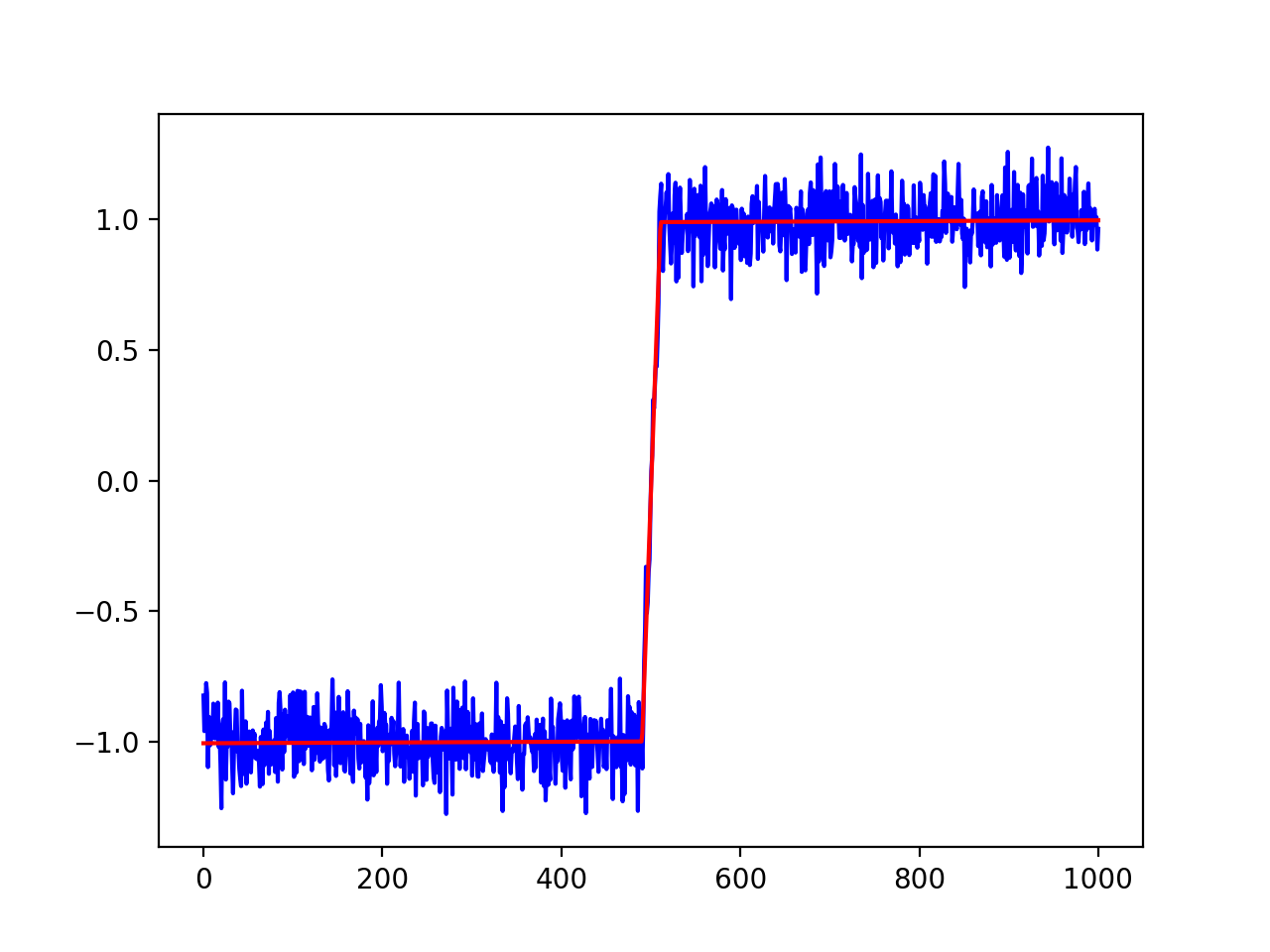
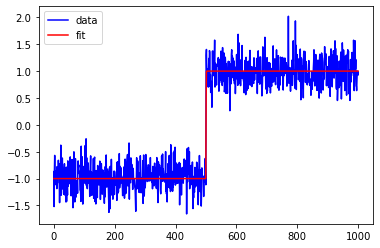
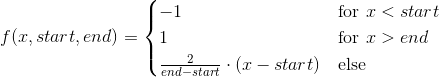The warning (not error) of

OptimizeWarning: Covariance of the parameters could not be estimated

means that the fit could not determine the uncertainties (variance) of the fitting parameters.

The main problem is that your model function f treats the parameters start and end as discrete values -- they are used as integer locations for the change in functional form. scipy's curve_fit (and all other optimization routines in scipy.optimize) assume that parameters are continuous variables, not discrete.

The fitting procedure will try to take small steps (typically around machine precision) in the parameters to get a numerical derivative of the residual with respect to the variables (the Jacobian). With values used as discrete variables, these derivatives will be zero and the fitting procedure will not know how to change the values to improve the fit.

It looks like you're trying to fit a step function to some data. Allow me to recommend trying lmfit (https://lmfit.github.io/lmfit-py) which provides a higher-level interface to curve fitting, and has many built-in models. For example, it includes a StepModel that should be able to model your data.

For a slight modification of your data (so that it has a finite step), the following script with lmfit can fit such data:

#!/usr/bin/python
import numpy as np
from lmfit.models import StepModel, LinearModel
import matplotlib.pyplot as plt

np.random.seed(0)
xdata = np.linspace(0., 1000., 1000)
ydata = -np.ones(1000)
ydata[500:1000] = 1.
# note that a linear step is added here:
ydata[490:510] = -1 + np.arange(20)/10.0
ydata = ydata + np.random.normal(size=len(xdata), scale=0.1)

# model data as Step + Line
step_mod = StepModel(form='linear', prefix='step_')
line_mod = LinearModel(prefix='line_')

model = step_mod + line_mod

# make named parameters, giving initial values:
pars = model.make_params(line_intercept=ydata.min(),
                         line_slope=0,
                         step_center=xdata.mean(),
                         step_amplitude=ydata.std(),
                         step_sigma=2.0)

# fit data to this model with these parameters
out = model.fit(ydata, pars, x=xdata)

# print results
print(out.fit_report())

# plot data and best-fit
plt.plot(xdata, ydata, 'b')
plt.plot(xdata, out.best_fit, 'r-')
plt.show()

which prints out a report of

[[Model]]
    (Model(step, prefix='step_', form='linear') + Model(linear, prefix='line_'))
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 49
    # data points      = 1000
    # variables        = 5
    chi-square         = 9.72660131
    reduced chi-square = 0.00977548
    Akaike info crit   = -4622.89074
    Bayesian info crit = -4598.35197
[[Variables]]
    step_sigma:      20.6227793 +/- 0.77214167 (3.74%) (init = 2)
    step_center:     490.167878 +/- 0.44804412 (0.09%) (init = 500)
    step_amplitude:  1.98946656 +/- 0.01304854 (0.66%) (init = 0.996283)
    line_intercept: -1.00628058 +/- 0.00706005 (0.70%) (init = -1.277259)
    line_slope:      1.3947e-05 +/- 2.2340e-05 (160.18%) (init = 0)
[[Correlations]] (unreported correlations are < 0.100)
    C(step_amplitude, line_slope)     = -0.875
    C(step_sigma, step_center)        = -0.863
    C(line_intercept, line_slope)     = -0.774
    C(step_amplitude, line_intercept) =  0.461
    C(step_sigma, step_amplitude)     =  0.170
    C(step_sigma, line_slope)         = -0.147
    C(step_center, step_amplitude)    = -0.146
    C(step_center, line_slope)        =  0.127

and produces a plot of

Lmfit has lots of extra features. For example, if you want to set bounds on some of the parameter values or fix some from varying, you can do the following:

# make named parameters, giving initial values:
pars = model.make_params(line_intercept=ydata.min(),
                         line_slope=0,
                         step_center=xdata.mean(),
                         step_amplitude=ydata.std(),
                         step_sigma=2.0)

# now set max and min values for step amplitude"
pars['step_amplitude'].min = 0
pars['step_amplitude'].max = 100

# fix the offset of the line to be -1.0
pars['line_offset'].value = -1.0
pars['line_offset'].vary = False

# then run fit with these parameters
out = model.fit(ydata, pars, x=xdata)

If you know the model should be Step+Constant and that the constant should be fixed, you could also modify the model to be

from lmfit.models import ConstantModel
# model data as Step + Constant
step_mod = StepModel(form='linear', prefix='step_')
const_mod = ConstantModel(prefix='const_')

model = step_mod + const_mod

pars = model.make_params(const_c=-1,
                         step_center=xdata.mean(),
                         step_amplitude=ydata.std(),
                         step_sigma=2.0)
pars['const_c'].vary = False

Jolley

Thanks, works like a charm. Can you point me in the right direction how to set the bounds and fix the parameter to a certain value (e.g. line_intercept to exactly -1)? – Crossroad

@Crossroad I edited the answer to show how to set bounds and fix parameter values. – Jolley

HA - if only every answer had the reply, "works like a charm" as this one does. – Shotton

Answer 2

This answer is way too late but if you want to stick to curve_fit from scipy, then re-writing the function to make it not explicitly depend on start and end as cutoff points does the job. For example, if x < start, then -1 can be written by shifting x by start and checking its sign, i.e. np.sign(x - start). Then it becomes a matter of writing a separate definition for each condition of the function and adding them up into a single function.

def f(x, start, end):
    left_tail = np.sign(x - start)
    left_tail[left_tail > -1] = 0         # only -1s are needed from here
    right_tail = np.sign(x - end)
    right_tail[right_tail < 1] = 0        # only 1s are needed from here
    rest = 1 / (end-start) * (x - start)
    rest[(rest < 0) | (rest > 1)] = 0     # only the values between 0 and 1 are needed from here
    return left_tail + rest + right_tail  # sum for a single value

popt, pcov = curve_fit(f, xdata, ydata, p0=[495., 505.])

The above function can be written substantially more concisely using np.clip() (to limit the values in an array) which can replace the boolean indexing and replacing done above.

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

def f(x, start, end):
    left_tail = np.clip(np.sign(x - start), -1, 0)
    rest = np.clip(1 / (end-start) * (x - start), 0, 1)
    return left_tail + rest

# sample data (as in the OP)
xdata = np.linspace(0, 1000, 1000)
ydata = np.r_[[-1.]*500, [1]*500]
ydata += np.random.normal(0, 0.25, len(ydata))

# fit function `f` to the data
popt, pcov = curve_fit(f, xdata, ydata, p0=[495., 505.])
print(popt, pcov)

# plot data along with the fitted function
plt.plot(xdata, ydata, 'b-', label='data')
plt.plot(xdata, f(xdata, *popt), 'r-', label='fit')
plt.legend();

# [499.4995098  501.51244722] [[ 1.24195553 -0.25654186]
#  [-0.25654186  0.2538896 ]]

Then using data constructed in the same way as in the OP, we get coefficients (499.499, 501.51) (that are pretty close to (500, 500)) and the plot looks like below.

Pignus