Plot scikit-learn (sklearn) SVM decision boundary / surface

Question

I am currently performing multi class SVM with linear kernel using python's scikit library. The sample training data and testing data are as given below:

Model data:

x = [[20,32,45,33,32,44,0],[23,32,45,12,32,66,11],[16,32,45,12,32,44,23],[120,2,55,62,82,14,81],[30,222,115,12,42,64,91],[220,12,55,222,82,14,181],[30,222,315,12,222,64,111]]
y = [0,0,0,1,1,2,2]

I want to plot the decision boundary and visualize the datasets. Can someone please help to plot this type of data.

The data given above is just mock data so feel free to change the values. It would be helpful if at least if you could suggest the steps that are to followed. Thanks in advance

Latt

See sklearn.inspection.DecisionBoundaryDisplay, Plot the decision boundaries of a VotingClassifier, Plot the decision surface of decision trees trained on the iris dataset – Millwater

Visualizations - Available Plotting Utilities – Tear

Answer 1

You have to choose only 2 features to do this. The reason is that you cannot plot a 7D plot. After selecting the 2 features use only these for the visualization of the decision surface.

(I have also written an article about this here: https://towardsdatascience.com/support-vector-machines-svm-clearly-explained-a-python-tutorial-for-classification-problems-29c539f3ad8?source=friends_link&sk=80f72ab272550d76a0cc3730d7c8af35)

---

Now, the next question that you would ask: How can I choose these 2 features?. Well, there are a lot of ways. You could do a univariate F-value (feature ranking) test and see what features/variables are the most important. Then you could use these for the plot. Also, we could reduce the dimensionality from 7 to 2 using PCA for example.

---

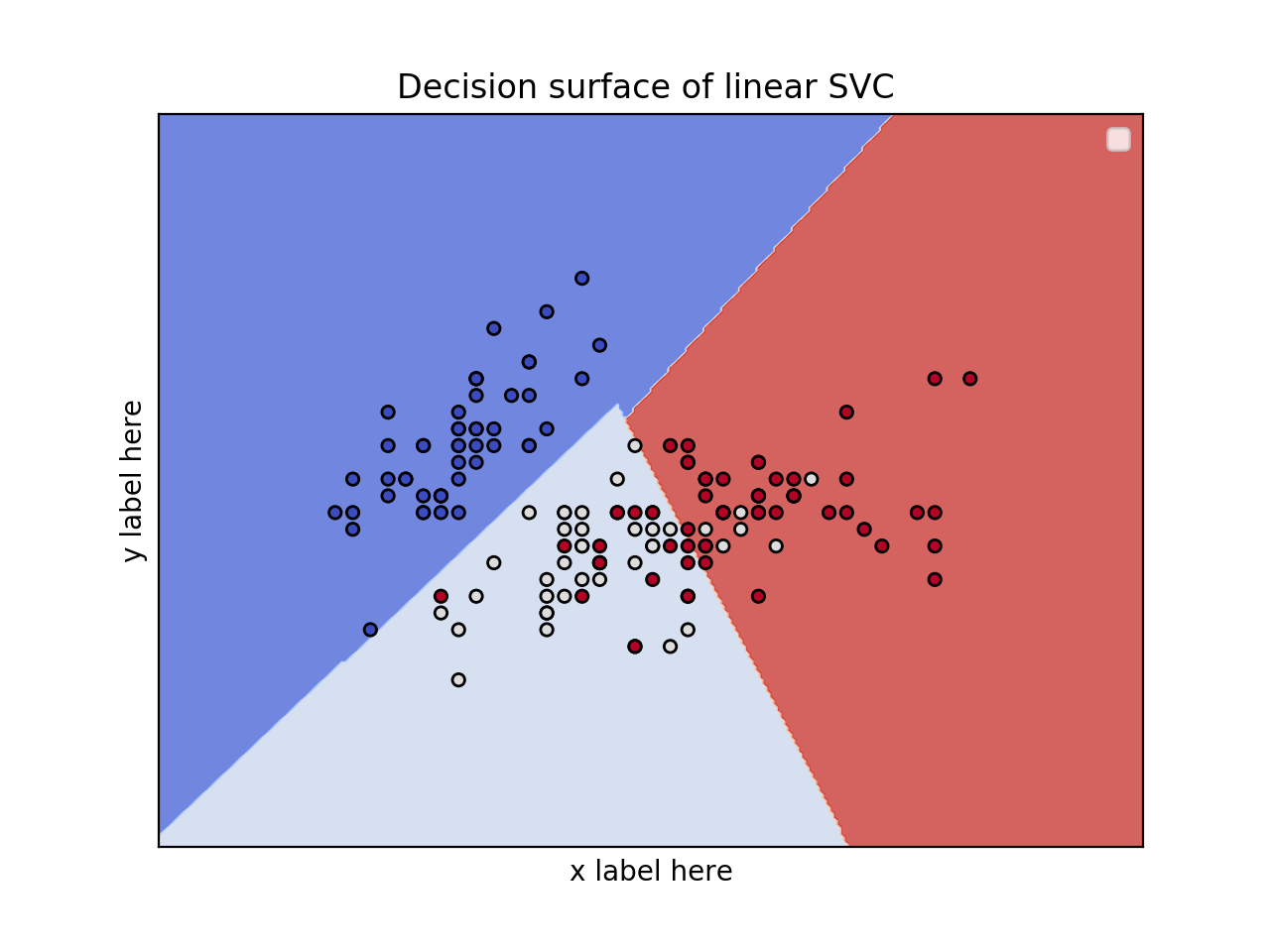
2D plot for 2 features and using the iris dataset

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets

iris = datasets.load_iris()
# Select 2 features / variable for the 2D plot that we are going to create.
X = iris.data[:, :2]  # we only take the first two features.
y = iris.target

def make_meshgrid(x, y, h=.02):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out

model = svm.SVC(kernel='linear')
clf = model.fit(X, y)

fig, ax = plt.subplots()
# title for the plots
title = ('Decision surface of linear SVC ')
# Set-up grid for plotting.
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)

plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_ylabel('y label here')
ax.set_xlabel('x label here')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
ax.legend()
plt.show()

---

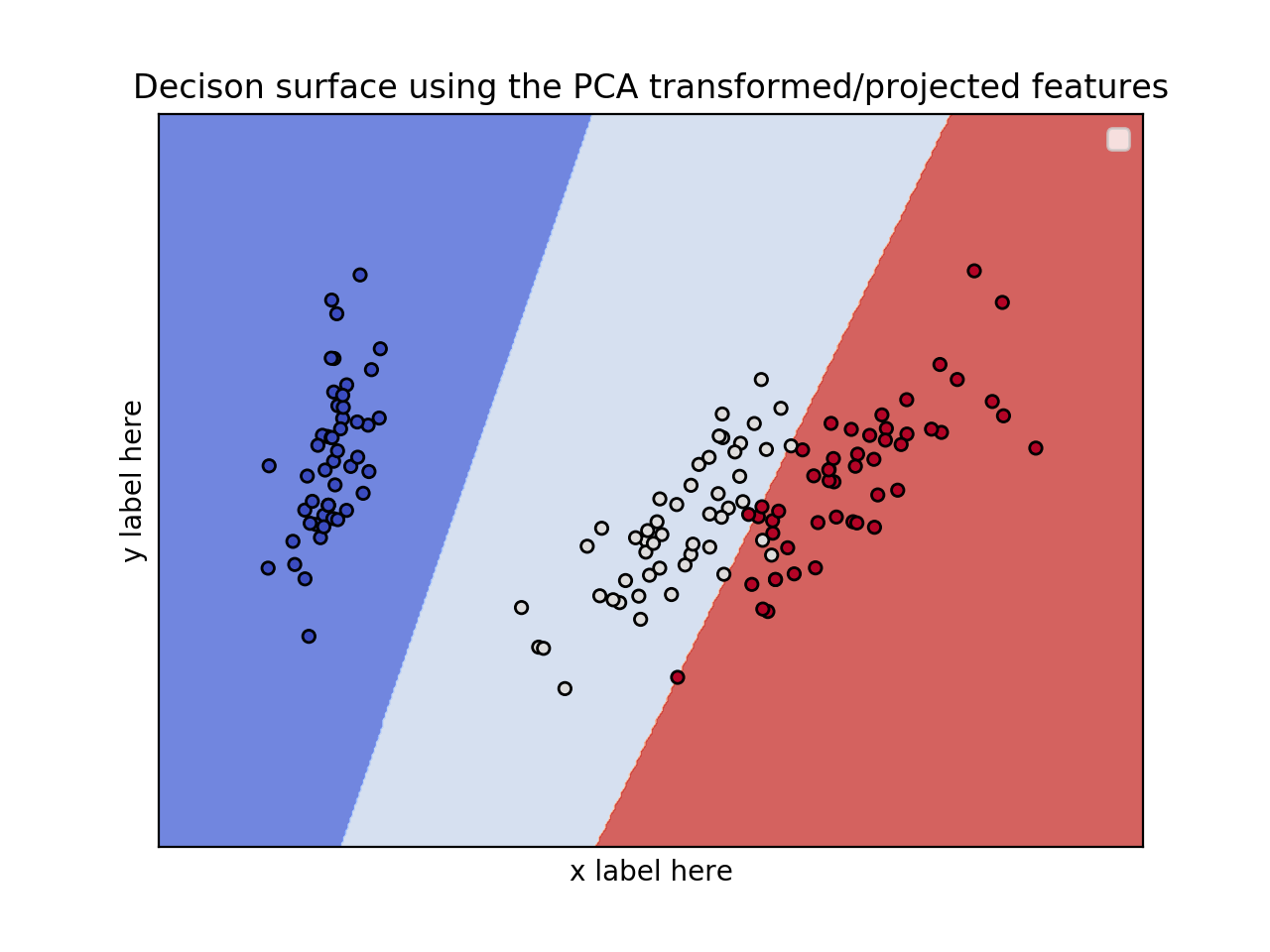
EDIT: Apply PCA to reduce dimensionality.

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from sklearn.decomposition import PCA

iris = datasets.load_iris()

X = iris.data  
y = iris.target

pca = PCA(n_components=2)
Xreduced = pca.fit_transform(X)

def make_meshgrid(x, y, h=.02):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    return xx, yy

def plot_contours(ax, clf, xx, yy, **params):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out

model = svm.SVC(kernel='linear')
clf = model.fit(Xreduced, y)

fig, ax = plt.subplots()
# title for the plots
title = ('Decision surface of linear SVC ')
# Set-up grid for plotting.
X0, X1 = Xreduced[:, 0], Xreduced[:, 1]
xx, yy = make_meshgrid(X0, X1)

plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_ylabel('PC2')
ax.set_xlabel('PC1')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title('Decison surface using the PCA transformed/projected features')
ax.legend()
plt.show()

---

EDIT 1 (April 15th, 2020):

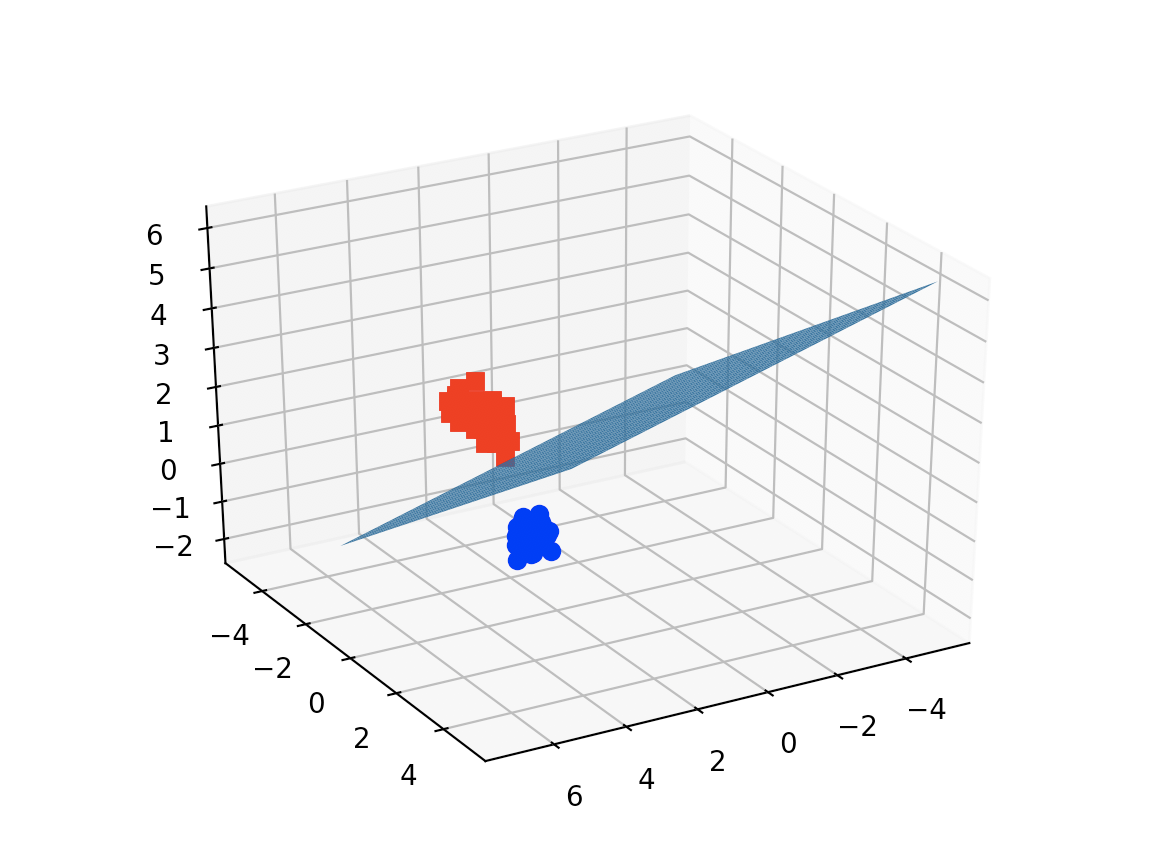
Case: 3D plot for 3 features and using the iris dataset

from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
from mpl_toolkits.mplot3d import Axes3D

iris = datasets.load_iris()
X = iris.data[:, :3]  # we only take the first three features.
Y = iris.target

#make it binary classification problem
X = X[np.logical_or(Y==0,Y==1)]
Y = Y[np.logical_or(Y==0,Y==1)]

model = svm.SVC(kernel='linear')
clf = model.fit(X, Y)

# The equation of the separating plane is given by all x so that np.dot(svc.coef_[0], x) + b = 0.
# Solve for w3 (z)
z = lambda x,y: (-clf.intercept_[0]-clf.coef_[0][0]*x -clf.coef_[0][1]*y) / clf.coef_[0][2]

tmp = np.linspace(-5,5,30)
x,y = np.meshgrid(tmp,tmp)

fig = plt.figure()
ax  = fig.add_subplot(111, projection='3d')
ax.plot3D(X[Y==0,0], X[Y==0,1], X[Y==0,2],'ob')
ax.plot3D(X[Y==1,0], X[Y==1,1], X[Y==1,2],'sr')
ax.plot_surface(x, y, z(x,y))
ax.view_init(30, 60)
plt.show()

Kubiak

I cant choose two features, because it is a sequence of data. I came across something called as ''dimension reduction technique" in the following link stats.stackexchange.com/a/155158 . But I am yet to figure it out. It has been said that if linear SVM is used, then data can be reduced to 2-dimensions using algorithms such as PCA. – Latt

yes this is exactly what I mentioned in my answer. You can either select 2 or do PCA for example to reduce to 2 dimensions and then use the projected data (reduced dimemensions = 2) to feed them in the SVM and finally plot the decision surface. Do you want me to update my answer using PCA? – Kubiak

Answer 2

You can use mlxtend. It's quite clean.

First do a pip install mlxtend, and then:

from sklearn.svm import SVC
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions

svm = SVC(C=0.5, kernel='linear')
svm.fit(X, y)
plot_decision_regions(X, y, clf=svm, legend=2)
plt.show()

Where X is a two-dimensional data matrix, and y is the associated vector of training labels.

Quittor

Answer 3

SVM-Decision-Boundary-Animator

The SVM-Decision-Boundary-Animator GitHub repo animates the SVM Decision Boundary Hyperplane on the Iris data using matplotlib

Repository consists of a script file, hyperplane generator function and the gif file.

1. Script File: Loads, normalises, and organises the Iris dataset from Sklearn package. Then generates an SVM model. Rather than feeding all the data, it dynamically samples into the training set one-by-one to see how training accuracy and the decision boundary hyperplane parameters vary over time. Finally it animates the varying parameters and saves in a gif file.

2. Hyperplane generator: A function to generate SVM decision boundary hyperplane

Following animation is generated by the script file, samples with black edges are the support vectors:

Below animation compares the learning paths of Radial Basis Function (RBF) and Linear kernels. No parameter tuning was made, default values of C=1, gamma="Auto" are used:

Adaiha